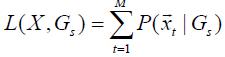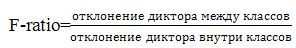|
Надежность идентификации диктора, основанная на перцептивном логарифмическом отношении площадей и модели Гауссовых смесей (перевод статьи: Кулибаба О.В., язык русский) Авторы: David Chow, Waleed H. Abdulla Источник: http://www.ele.auckland.ac.nz/~wabd002/ICSLP%20Speaker%20ID%20as%20submitted.pdf Аннотация Эта статья представляет новый признак для идентификации дикторов, который называется перцептивное логарифмическое отношение площадей (PLAR– perceptual log area ratio). PLAR тесно связано с признаком LAR (log area ratio). PLAR получено из перцептивного линейного предсказания (perceptual linear prediction – PLP), точнее из линейного кодирования с предсказанием ( linear predictive coding – LPC). Признак PLAR, полученный из PLP, более устойчив к шуму, чем LAR. В этой PLAR, LAR и MFCC признаки будут протестированы на модели Гауссовых смесей (Gaussian mixture model – GMM), основанной на системе идентификации диктора. Анализ признака F-ratio показал, что нижний порядок PLAR и LAR коэффициентов превосходит в классификации производительность их MFCC копии. Точности текст–независимой и идентификация на замкнутом множестве, протестированные на KING, YOHO и последней версии TIMIT базах данных, 98.81%, 85.29%, 97.045%, при использовании PLAR, 97.92%, 61.76%, 94.76%, при использовании LAR и 96.73%, 84.31%, 96.48%, при использовании MFCC. Эти результаты показывают, что PLAR лучше, чем LAR и MFCC и в тихой, и в шумной обстановке. Введение Выделение признаков – это главное в предварительной обработке данных в системах идентификации дикторов. Производительность системы идентификации дикторов сильно зависит от качества выбранных речевых признаков. Большинство популярных систем идентификации предлагают использовать мел-частотные кепстральные коэффициенты (MFCC) и линейные предсказывающие кепстральные коэффициенты (LPCС) как вектор признаков[1]. В настоящее время исследования сфокусированы на повышении качества этих двух кепстральных признаков [2] или дополнении их новыми признаками [3]. Доказано, что алгоритмы MFCC и LPCС – двое наиболее хороших признаков в распознавании речи, они не обязательно лучшие в распознавании дикторов. По сути, обычно полагают, что спектральное сглаживание, сделанное MFCC и LPCС, имеет некоторую разновидность нормализации дикторов. Для речевого признака, использующегося в идентификации диктора, будет эффективнее, если он будет отражать уникальные свойства речевого аппарата диктора и включать мало или не включать информацию о лингвистическом содержании речи[4]. Коэффициенты линейного кодирования с предсказанием (LPC) включают ценную информацию о дикторе и ее производные, логарифмическое отношение площадей (LAR) имеет такие же характеристики. Признак LAR лучше, чем LPC при идентификации дикторов, потому что он имеет линейную спектральную чувствительность и он более устойчив к шуму квантования [5]. В стороне от этого, GSM кодируют речь, используя признак LAR. Поэтому, LAR наиболее совместимый с GSM кодированием речи, чем MFCC. Однако, LPC сильно чувствительны к шуму, который делает их вторичными, LAR также чувствительны к шуму. В этой статье мы охватим проблему извлечения LAR коэффициентов с PLP вместо LPC. Новый признак называется перцептивное логарифмическое отношение площадей (PLAR). PLР очень похож на LPC, предполагается что он захватывает человеческое поведение в основе. Показано, что PLP устойчивы к шумам. Таким образом, мы верим, что PLAR также будет устойчив к шумам. В 1995 году Рейнольдс продемонстрировал, что Гауссова смешанная модель (GMM) на основе классификатора хорошо работает в тексто-независимой идентификации диктора даже с речевым признаком, который включает ценную лингвистическую информацию, как MFCC [3,7]. С вышесказанными результатами, авторы полагают, что использование PLAR, основанного на признаках таких, как признак векторов в GMM системах распознавания дикторов, дает хорошие результаты идентификации. В этой статье производительность признака PLAR изучена полностью при помощи анализа F-ratio. Рассмотрены серии экспериментов о производительности признака PLAR в системе идентификации диктора. Статья организована, как изложено ниже; в секции 2 описание LAR признака. Секция 3 объясняеет GMM систему распознавания дикторов, использующую в этой статье. Секция 4 сравнивает производительность PLAR, LAR и MFCC признаков. Секция 5 извлекает выводы из этой работы. 2 Коэффициенты перцептивного логарифмического отношения площадей PLAR коэффициенты близко связаны с LAR коэффициентами, которые получены из LPC. LPC базированный признак – высокоэффективное представление речевых сигналов. В этом отношении каждый речевой образец представлен взвешенной суммой р последних образцов речи плюс соответствующее возбуждение. Соответствующая формула для LPC модели:
Где р – порядок LPC фильтра,sn – это n-й речевой образец и akэто k – коэффициент LPC вектора. Эти коэффициенты найдены по алгоритму Дурбина, который минимизирует среднюю площадь ошибки предсказания модели [5,8]. Автокорреляционную матрицу необходимо найти перед применением алгоритма Дурбина. Автокорреляционная матрица может быть найдена в частотной области. Вычисление PLP коэффициентов похоже на вычисление LPC коэффициентов, предполагается, что когда вычисляется автокорреляционная матрицы, три шага должны получить отражение человеческого восприятия звука. Эти три шага [9]:
Таким образом, PLP модель может быть рассмотрена, как расширенная LPC модель, которая может лучше охарактеризовать речевой тракт человека. Она может быть также преобразована в другие коэффициенты, подобно как LAR называют PLAR. В PLAR анализе речевой тракт смоделирован как неоднородная акустическая труба, сформированная с каскада р однородных равной длины цилиндровых труб с разными площадями поперечных сечений. Глотка соединена с первой трубой, которая имеет нулевую площадь, губы соединены с последней трубой, которая имеет бесконечную площадь. Рисунок 2.1 иллюстрирует акустические трубы речевой модели
Рисунок 2.1 – Акустические трубы речевой модели В этой модели длина каждой цилиндрической трубы вплотную связана с периодом дискретизации и числом коэффициентов PLP модели. Поэтому при вычислении PLAR коэффициентов длина речевого тракта не должна быть точно определена. PLAR коэффициенты формируются как логарифмическое отношение площади между площадями поперечных сечений каждых двух соединенных труб. Количество цилиндрических труб в модели равно количеству PLAR коэффициентов плюс один. Зависимость между PLAR и PLP коэффициентами:
Где
Где 3 Модель Гауссовых смесей основана на системе идентификации диктора В исследовании системы идентификации диктора, каждый диктор регистрировался в системе, представленной Гауссовой смешанной моделью (GMM). Цель GMM – использование серии гауссовых функцый для представления вероятности плотности вектора признаков, представляемого каждого диктора. Математическое представление:
Где М – это количество смесей, х – это вектор признаков, wi – вес i-й смеси в GMM, В фазе идентификации, сумма логарифмической вероятности входящей частоты вектора признаков как объект каждой модели диктора:
Где х – это частота вектора признаков диктора и М – целое число признаков вектора. GMM, которое сгенерировало наибольшее L(X,Gs)идентифицирует входящий речевой сигнал. Этот решающий метод называется максимизацией вероятности (ML) 4 Определение производительности PLAR Три эксперимента были проведены на трех различных базах данных. Речевой сигнал был получен при помощи энергии на основе алгоритма. Фильтер без предыскажения был применен к сигналу. Анализ речевого сигнала проводился с речевыми кадрами, длиной 20мс с 10мс перекрытием. Оконная функция использовала окно Хэмминга. Длина окна выбиралась так, чтобы речевых образцов было достаточно в каждом кадре для оценки речевого спектрума, и сделать его нечувствительным к размещению окна, относительно высоты периодов. Инструмент классификации, использующийся в этом эксперименте основывался на 32 смесях GMM классификатора, инициализированного вектором квантования (VQ)[11] 4.1 Производительность с базой данных TIMIT TIMIT – это зашумленная бесплатная речевая база данных (53дБ отношение сигнал/шум), записанная с использованием высококачественного микрофона с дискретизацией 16кГц. В этой статье все 168 дикторов в тестовой базе TIMIT были задействованы в эксперименте. Речевой сигнал проходил сначала через 30–порядковый FIR фильтр нижних частот, потом выбирались нижние частоты от 16кГц до 8кГц. В TIMIT каждый диктор произносит 10 фраз, первые 8 фраз используются для обучения, а последние 2 для тестирования. Средняя длина каждой фразы – 3 сек. Другими словами, приблизительно 24 сек речи для обучения и 6 сек для двух тестов 4.1.1 F-ratio анализ в TIMIT F-ratio – это отношение качества оценки эффективности к коэффициентам, и может быть сформулировано как:
На рис 4.1 сравнивается F-ratio PLAR, LAR и MFCC признаков. Этот рисунок показывает, что нижний порядок коэффициентов PLAR и LAR признаков имеет выше значение F-ratio, чем соответстующие MFCC. Для тексто-независимой идентификации диктора, значение F-ratio хорошо показывает качество признаков, несмотря на 3 предположения, требующие F-ratio не в полном объеме. Эти 3 предположения:
Рисунок 4.1 – Значения F-ratio для PLAR, LAR и MFCC признаков 4.1.2 Результаты идентификации для TIMIT Работа Рейнольдса [7, 13] была восспроизведена и использована в качестве основы системы оценивающей производительность предложеного PLAR признака. Сравнительные результаты представлены в таблице 4.1. Там можно увидеть, что точность идентификации диктора получена при использовании предложенного признака при полной TIMIT (т.е. 0 – 8000Гц) – это почти то же, что получил Рейнольдс. Количество коэффициентов, использованных в векторе признаков – 20.
Таблица 4.1 – Процент идентификации MFCC базированной системы идентификации диктора на TIMIT речи
Во втором эксперименте с TIMIT нижнее перекрытие только 4000Гц. На рис. 4.2 показано, что процент идентификации, основанный на 18, 20, 22 и 23 коэффициентах вектора признаков PLAR лучше. Мы выбрали 20 коэффициентов, чтобы длину векторов признаков можно было сопоставить с работой Ренольдса, где было выбрано 20 коэффициентов. Таблица 4.2 сравнивает процент идентификации, использующий 20 PLAR, 20 LAR и 20 MFCC коэффициентов. Там также показан процент идентификации, полученный в работе Ренольдса. Из этой таблицы видно, что процесс идентификации, использующий MFCC – 96.73% сравним с 98.81% с применением PLAR. Достигается 2.08% улучшение. Результаты идентификации, полученые в этой статье, использующие MFCC на базе данных TIMIT выше (96.73%), чем полученные Рейлнольдом (95.2%), несмотря на то, что мы повторили этот эксперимент. Вероятная причина – это то, что он использовал телефонную полосу пропускания(300 – 3400Гц), а мы в этой статье использовали намного шире (0–4000Гц) полосу.
Таблица 4.2 – Процент идентификации признаков PLAR, LAR и MFCC
4.2 Производительность с базой данных KING Существует 2 версии записей в базе данных KING. Одна записана через микрофон, а другая записана через телефон. Телефонные записи содержат шум. Половина речевых образцов имеет 10–20дБ отношение сигнал/шум, другая приблизительно 30дБ отношение сигнал/шум. Обе записи были дискретизированы с частотой 8кГц. В этой статье, все 51 диктор телефонной версии базы данных KING участвовали в эксперименте. В KING каждый диктор произносил 10 ссесий записей, первые 3 сессии были использованы для обучения, а последние 2 – для тестирования. Для речевых образцов в базе данных KING, которая была записана в Сан–Диего, спектральное искажение было в сессиях 1–5 – это очень отличалось с первой в сессиях 6–10. Поэтому, только первые 5 сессий были использованы в этой статье. В этом эксперименте все признаки подвергались кепстральной средней нормализации (CMN) для удаления эффекта канального несоответствия и адитивного шума. Обычно, CMN часто применяет кепстральные признаки в порядке перемещения канального эффекта. Однако, ухудшение речи в KING главным образом возникает от аддитивного шума, и применяя CMN процесс для MFCC, LAR и PLAR признаков, уменьшаем адитивный шумовой эффект. Речевой сигнал, ограниченный полосой 300–3400Гц применялся для выборки всех трех признаков. Таблица 4.3 представляет точность идентификации использования трех признаков. Она также включает результат Рейнольдса для сравнения. Из таблицы видно, что точность идентификации, полученная PLAR – 85.29%, лучше чем MFCC. Кроме того, можно увидеть что признак LAR представляет плохо шумовую речь. Таблица 4.3 Процесс идентификации признаками PLAR, LAR и MFCC.
4.3 Производительность с базой данных YOHO Речевая база данных YOHO записана с использованием телефонной трубки под реальное офисную среду с частотой дискретизации 8кГц (43дБ отношение сигнал/шум). В этой статье все 138 дикторов YOHO участвовали в эксперименте. YOHO – это словарь, содержащий речевую базу данных, которая содержит только комбинации парольных фраз. Все фразы в папке «ENROLL» были использованы для обучения системы, и каждая фраза в папке «VERIFY» была использована для тестирования. Поэтому, около 6 мин речи использовалось для обучения и 2.4 сек использовались при каждом тестировании. 40 тестов по дикторам проводилось в нашем эксперименте. Таблица 4.4 показывает точность идентификации при использовании трех различных признаков. Из таблицы видно, что точность идентификации, полученная при использовании PLAR 97.05%, которая незначительно выше, чем при использовании MFCC – 96.48%. Высокая точность получается при использовании LAR – 94.76%, которая меньше чем PLAR и MFCC. Это предположено, как LAR чувствителен к шуму в этом источнике. Таблица 4.4 Процент идентификации в базе данных YOHO, использующую признаки PLAR, LAR и MFCC
5 Выводы В этой статье мы продемонстрировали новый признак для системы идентификации дикторов, называемый PLAR. При использовании 20 коэффициентов PLAR процент идентификации 98.81% достигнут в сравнении с 96.73% при применении подобного MFCC признака, использующего зашумленную бесплатную базу данных (TIMIT, 53дБ отношение сигнал/шум) и полосу пропускания 4кГц. LAR получились вторыми в этом эксперименте, достигнув процента идентификации 97.97%. Кроме того, признак PLAR превосходит LAR и MFCC признаки, когда используется высокозашумленная речевая база данных (KING, 10–30дБ отношение сигнал/шум), таблица 4.3 и умеренный шум в речевой базе данных (YOHO, 43дБ отношение сигнал/шум), таблица 4.4. Этот эксперимент доказал, что признак PLAR устойчив к шуму. F-ratio анализ показал, что нижний порядок PLAR коэффициентов более эффективный, чем нижний порядок MFCC коэффициентов в записанной диктором информации. PLAR аналогично LAR более совместимы с GSM кодированием речи, чем MFCC, который меньше PLAR имеет потенциальную возможность быть использованным в мобильной системе идентификации диктора. 6 Благодарности Эта работы выполнена при поддержке вице премьер–министра фонда развития университета Окленда, проект 23109, и исследовательского фонда университета Окленда, проект 3602239/9273. 7 Литература
|
|||||||||||||||||||||||||||||||||||||||||||||||||
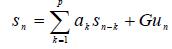

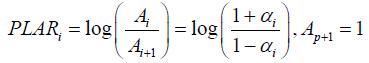
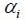 – это ith PLP базированный коэффициент, который может быть найден как:
– это ith PLP базированный коэффициент, который может быть найден как:

 – это ith PLP коэффициент, вычисленный из i – го порядка PLP модели.
– это ith PLP коэффициент, вычисленный из i – го порядка PLP модели.
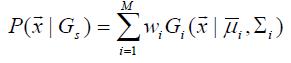
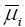 – это среднее i-й смеси в GMM и
– это среднее i-й смеси в GMM и
 –это ковариационная матрица i-й смеси в GMM [3,7]. Параметры модели характеризуют голос диктора в форме функции плотности вероятности. Они определяются алгоритмом ЕМ [10].
–это ковариационная матрица i-й смеси в GMM [3,7]. Параметры модели характеризуют голос диктора в форме функции плотности вероятности. Они определяются алгоритмом ЕМ [10].