Для решения задач САПР требуется модель, адекватно отображающая поведение логической схемы и удобная при машинной реализации.
Для дальнейшего рассуждения определимся в основных понятиях. Логическая схема называется комбинационной (КС), если значения ее
выходов зависят только от значений ее входов. Логическая схема называется последовательностной (ПС), если значения ее выходов
зависят как от значений ее входов, так и от их предыстории, другими словами, ПС – это схема с обратными связями.
На основании проведенных исследований и практики проектирования и анализа цифровых систем в качестве модели логической
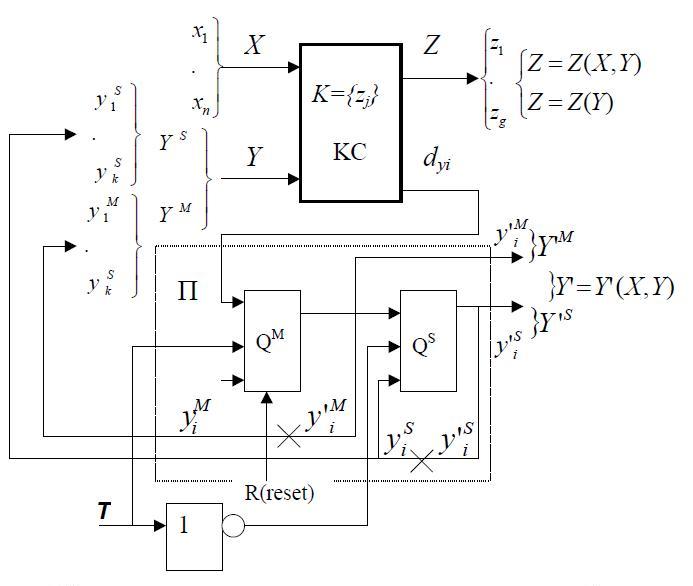
схемы предлагается модель, представленная на рисунке. В отличие от классической модели Хаффмана, предлагаемая модель
учитывает современные тенденции в схемо- и системотехнике, в частности, применение двухступенчатых триггеров (M-S); синхронизацию
(при этом если синхросигнал не отличать от других входов схемы, то модель будет отображать основной класс асинхронных схем); понятие
сигнала системного сброса (начальной установки) и др. Это значительно уточняет модель при использовании машинно-ориентированных
методов проектирования и анализа схем.
Модель схемы условно разбита на комбинационную и последовательностную (П) части. Здесь вектор Х есть независимые входы
схемы, из которых особо выделены сигнал синхронизации Т и сигнал начальной установки элементов памяти R, который может быть как
асинхронным сбросом, так и синхронизированным тактом Т, что в общем случае не является принципиальным. Значения Y’ определены
как булевы функции Y’ = Y’(X,Y). Значение сигналов обратной связи Y разбито на два подмножества YM и YS, соответственно Y’ = Y’MU Y’S.
Значения выходных сигналов также определены как Z = Z( X,Y ) для автомата Мили и как Z = Z(Y) для автомата Мура. Для схемы также
определены некоторые промежуточные сигналы Zj как выходы КС, которые являются вспомогательными и введены как следствие разбиения
КС на одновыходные комбинационные подсхемы или с целью уменьшения размерности решаемых задач. Значение вектора сигналов Y
определяет предыдущее значение состояния схемы, а значение вектора Y’ – последующее состояние. В общем случае векторы Y и Y’
задают некоторые классы состояний. Любой сигнал y и y’ может принимать три значения: 0, 1 и х, где х есть безразличное состояние,
которое произвольным образом можно доопределить в значение 1 или 0, если это не вызывает противоречия при переходе схемы из
состояния Y в состояние Y’.
Соответствие между значениями сигналов Y и Y’ определяется по интервальным кубическим покрытиям C(y’ ) = Cx(y’ ) CUp(y’ ),
где Cx(y’ ) есть область установки, а Cp( y’ ) – область хранения. Если некоторое значение y’ вычислено кубом С ? Сх( y’ ),
то y = x и y’ = p, если же значение y’ вычислено кубом C ? Cp( y’ ), то значение y = y’ = p.
Универсальная модель последовательностной схемы
|
В соответствии с предложенной универсальной моделью схемы введём понятие куба единого формата Ф0 = X YM YS ZК Y’ M Y’ S Z. Данный
формат в векторном виде описывает все значения сигналов и их разбиение на функциональные классы. Если не делать различия между
классами YM, YS, Y’ М и Y’ S, то можно ограничиться форматом Ф1 = X Y ZК Y’ Z. Далее, если ZК отсутствуют, можно ограничиться
форматом Ф2 = X Y Y’ Z. Наконец, для случая, когда рассматриваются только переходы схемы, можно перейти к формату Ф3 = X Y Y’,
что является вполне допустимым при теоретическом рассмотрении состояний и переходов схемы, так как значения ZК и Z являются
импликациями от независимых входов Х и сигналов обратной связи Y или Y’, и их можно вычислить после построения переходов.
По предложенной универсальной модели, в отличие от модели функциональных неисправностей [4], могут быть решены не только
задачи синтеза тестовых последовательностей, но и следующие задачи САПР:
• моделирование;
• анализ состязаний;
• построение переходов схемы в прямом и в обратном направлении;
• верификации иерархических моделей;
• другие задачи анализа.
|