МОДЕЛЮВАННЯ ДИНАМІКИ РИНКОВИХ ЦІН НА БАЗІ НЕЛІНІЙНОЇ ПАВУТИНОВИДНОЇ МОДЕЛІ ЦІНОУТВОРЕННЯ ДЛЯ РИНКУ НЕРУХОМОСТІ

Моспан А.А.

Руководитель Назарова И.А.

Тринадцатая Всеукраинская (Восьмая Международная) Студенческая Научная Конференция по Прикладной Математики и Информатики, Направление: Моделирование задач экономики и финансов,
Львовский национальный университет имени Ивана Франко, 22 - 23 апреля 2010 г.

  Припускаємо, що всі будівельники мають приблизно однаковий рівень доходів і єдину ціль.

  Нехай ціна характеризується наступною нелінійною функцією, зворотною функції попиту: P=a-b√Q.

  Маємо попит на землю в період t – D1(t), попит на житло в період t – D2(t), і, відповідно, Р1 і Р2 – ціни на землю та житло. Таким чином функції попиту можна представити в наступному вигляді:

D1(t) = b0 - b1*P1(t) + b2*(P1(t))^2,    D2(t) = c0 - c1* P2(t) + c2*(P2(t))^2.

  Відповідно до закону попиту, крива попиту має незростаючий характер, і наведені залежності повинні відповідати умовам:

2b2*P1(t) - b1 < 0;     2c2*P2(t) - c1 < 0;    4b2b0 - (b1)^2 > 0;     4c2c0 - (c1)^2 > 0.

  У такому разі ринок землі і ринок житла взаємопов'язані. Потрібно зауважити, що ринок житла безпосередньо не впливає на ринок землі, ціни на землю впливають на пропозицію житла, яке знижується зі зростанням цін на землю. У такому випадку функції пропозиції земельних ділянок (S1) і житла (S2) у період t можуть бути наступними:

S1(t) = a0 + a1*P1(t) + a2*(P1(t))^2,    S2(t) = d0 + d1*P2(t) + d2*(P2(t))^2 - d3*P1(t).

  Відповідно до закону пропозиції, крива пропозиції має неубиваючий характер, і наведені залежності повинні відповідати умовам:

2a2*P2(t) + a1 > 0;    2d2*P2(t) + d1 > 0.

  Постачальники будуть доставляти продукцію в випадку, якщо:

P1(t) > (-a1 + √((a1)^2 - 4a2*a0))/(2a2);     P2(t) > (-d1 + √((d1)^2 - 4d2*d0))/(2d2).

  Визначу, Z(P) = D(P) -S(P). Z(P) - функція зайвого попиту, прямо пропорційно залежить від ціни, яка заповнює різницю між попитом і пропозицією. Коли ціна низька, надлишковий попит існує, і, коли ціна висока, надлишковий попит теж існує, таким чином, рівноважна ціна P*, яка задовольняє Z(P* )=0, називається точкою рівноваги.

  Підставляючи функції попиту і пропозиції до функції Z(P) отримаємо:

Z(P1(t)) = b0 - a0 - (a1 + b1)*P1(t) + (b2 - a2)*(P1(t))^2;
Z(P2(t)) = c0 - d0 - (d1 + c1)*P2(t) + (c2 - d2)*(P2(t))^2 + d3*P1(t);
t=0,1,2..

  Так як Z(P) залежить від функції попиту, то повинна задовольняти умовам:

b2 - a2 > 0;    c2 - d2 > 0;    2*(c2 - d2)*P2(t) - (d1 + c1) < 0;     2*(b2 - a2)*P1(t) - (a1 + b1) < 0.

  Динамічна модель цін на землю і житло може бути сформована таким чином:

P1(t) = P1*(t - 1) + α1*Z(P1(t-1));
P2(t) = P2*(t - 1) + α2*Z(P2(t-1));
t = 0,1,2…,

де α1—параметр ціни на землю, який коригує ціну на житло, контрольовану урядом за допомогою планів земельних ділянок; α2—параметр ціни на житло.

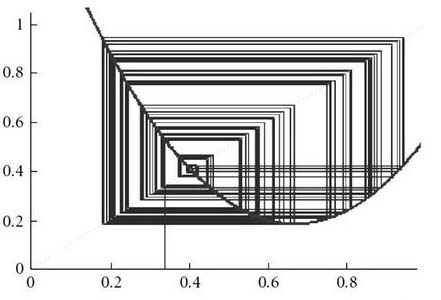
  Очевидно, що ці функції житла та землі з регулюючими параметрами є двомірним нелінійним простором, який може бути розглянутий як дискретна динамічна система. Приклад такої моделі з заданими параметрами зображено малюнку.

© Моспан А.А. 2010