Отображение рассматривают как функцию f, определенную на множестве Х, принимающее свои значения среди элементов множества Y и каждому элементу из Х может отвечать один и лишь один элемент из Y. Пару векторов XиY называют примером или реализацией.
В задачах отображения нейросети осуществляют оценивание и предсказание поведения объектов, в том числе систем и процессов, заданных определенными законами и совокупностью своих реализаций. Каждая реализация должна содержать набор признаков, определяющих основное содержание объекта. Если одним из признаков объекта исследования является время, тогда реализации могут быть представлены в виде временных рядов.
У большинства реальных объектов исследования можно выделить их основные составляющие:
- детерминированная составляющая, которая в принципе подлежит
точному предсказанию;
- вероятностная составляющая, которую можно предсказать с заданной
степенью вероятности;
- чисто случайная составляющая, которую невозможно ни учесть, ни предусмотреть.
- детерминированное множество данных, со всеми учтенными основными
параметрами, вызванными действием известных причин. Оно характеризуется
малым уровнем шумов;
- множество данных с наличием вереятностной составляющей, вытекающей
из экспериментальной постановки задачи, с разной степенью учета
действующих факторов и с влиянием погрешностей оценивания;
- множество данных с наличием случайной составляющей, вследствие неучтенных признаков явления.
Задачи отображения можно разбить на два основных класса:
- классификация;
- регрессия.
В задачах регрессии предусматривают значение переменной, принимающей непрерывные числовые значения: цена акций, затрата топлива в автомобиле, прибыль кампании и т.п.
Предвидение явлений можно поделить на:
- предвидение выходов для множества дискретных входных данных,
не связанных со временем (экономические, социологические оценки
и др.); данные представлены таблично;
- прогнозирование явлений, непрерывно изменяющихся во времени (физические процессы, естественные явления, и т.п.); данные представлены в виде временных рядов.
Сначала, выбор параметров осуществляется интуитивно. Опыт работы в предметной области поможет определить, какие переменные являются важными. Для начала имеет смысл включить все переменные, которые могут влиять на результат — на следующих этапах это множество можно сократить.
Для обеспечения обоснованного выбора и изъятия несущественных признаков, вносящих дополнительные искажения при обучении, возможно применение методов математической статистики.
Факторный анализ
Внос каждого входного признака можно оценить по его влиянию на среднее значение выходной величины. Пусть внешний выход модели нейросети зависит от нескольких факторов
y=f(a1x1, a2x2, ..., aixi...)
Выберем некоторый фактор аіхі. Для всех реализаций обучающего множества определим значения выходной величины при наличии и отсутствии этого фактора. Вычислим дисперсию, вызванную отсутствием фактора аіхі.
где Yxі*, Yxі — соответственно значение средней величины при отсутствии и наличии фактора аіхі.
Определяем интервал DaI=± 2Sai,куда не должна попадать оценка коэффициентов аі. При малых коэффициентах данный фактор изымается.
Корреляционный анализ
Некоторые из параметров, принимаемые во внимание, имеют незначительное влияние на формирование выходов и могут быть отброшены. В качестве показателя взаимозависимости между системой входных величин X=(X1, X2, ..., Xn) і выходных величин Y , можно выбрать коэфициент парной корреляции (например входной переменной X1 и выходного значения Y)
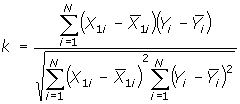
где
Значение k < 0,6 считают пороговым. Например, при нахождении коэффициентов корреляции между выходом и входами можно определить степень влияния каждого входного параметра на выход, и использовать данный показатель для ранжирования входов.
Ранжирование входов
При прогнозировании, существенным для качества является учет реального влияния каждого параметра входа x(х1, ..., хn) на выходной вектор y. С помощью корреляционного анализа заранее вычисляются коэффициенты парной корреляции между выходом y и каждым из параметров входа х1, ..., хj, ..., хn, что позволяет сформировать входную матрицу согласно степени влияния каждого параметра и применить принцип ранжирования входов, что согласовывается со строением биологического нейрона. В нейросеть вводится единый параметр для всех входов сети — коэффициент взвешивания Kf, принимающий значение в диапазоне от 0 до 1.
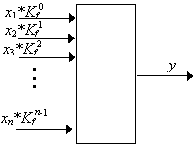
Рис. 1. Влияние коэффициента взвешивания входов
Для 1 входа все значения параметра х1 не изменяются, для 2 входа уменьшаются в Kf1 раз, а для последнего n-го входа вес параметра xn уменьшается в Kfn-1 раз (рис. 1). При Kf=1 все входы равнозначны, при Kf=0 учитывается лишь первый вход, остальные входы игнорируется, при 0<Kf<1 уменьшается влияние несущественных параметров на выходную величину y.
Такой подход требует проведения предварительного анализа информации, но значительное улучшение точности прогноза подтверждает его эффективность.
Выбор данных для обработки
Любая нейронная сеть принимает на входе числовые значения и выдает на выходе также числовые значения. Передаточная функция для каждого элемента сети обычно выбирается таким образом, чтобы ее входной аргумент мог принимать произвольные значения, а выходные значения лежали бы в строго ограниченном диапазоне. При любых входных значениях возникает эффект насыщения, когда элемент чувствителен лишь к входным значениям, лежщим в ограниченной области (например, S — функции). В этом случае выходное значение всегда будет лежать в интервале (0,1), а область чувствительности для входов едва шире интервала (-1,+1). Данная функция является гладкой, а ее производная легко вычисляется — это обстоятельство важно для работы алгоритма обучения сети (в этом также кроется причина того, что пороговая функция для этой цели практически не используется).
При использовании нейронных сетей могут возникать некоторые проблемы, в частности:
- данные имеют нестандартный масштаб,
- данные являются нечисловыми.
- в данных имеется пропущенное или недостоверное значение.
Более сложной задачей является работа с данными нечислового характера. Пусть, нужно научить нейросеть оценивать стоимость объектов недвижимости. Цена дома зависит от того, в каком районе города он расположен. Город может быть разделен на несколько десятков районов, имеющих собственные названия, и естественно ввести для обозначения района переменную с номинальными значениями. К сожалению, в этом случае научить нейронну сеть будет трудно, и вместо этого лучше присвоить каждому района определенный ранг (базируясь на экспертных оценках).
Чаще всего нечисловые данные представляют в виде номинальных переменных. Номинальные переменные могут быть двузначными (например, Пол ={Мужчина, Женщина}) или многозначными (то есть принимать больше двух значений). Двузначную номинальную переменную легко превратить в числовую (например, Мужчина = 0, Женщина = 1). С многозначными номинальными переменными сложнее. Их тоже можно представить одним числовым значениям (например, Собака = 0, Мышь = 1, Кошка = 2), однако при этом возможно ошибочное присвоение значений номинальной переменной: в рассмотренном примере Мышь окажется чем-то средним между Собакой и Кошкой. Существует более точный способ, известный как кодирование 1-из-N, в котором одна номинальная переменная представляется несколькими числовыми переменными. Количество числовых переменных равняется числу возможных значений номинальной переменной; при этом всякий раз только одна из N переменных принимает ненулевое значение (например, Собака = {1,0,0}, Мышь = {0,1,0}, Кошка = {0,0,1}). К сожалению, номинальная переменная с большим числом возможных состояний требует при кодировании методом 1-из-N очень большого количества числовых переменных, а это приводит к росту размеров сети и создает трудности при ее обучении. В таких ситуациях лучше попробовать найти другой способ представления данных.
Нечисловые данные других типов можно или превратить в числовую форму, или объявить незначительными. Значение дат и времени, если они нужны, можно превратить в числовые, отнимая из них начальную дату (время). Значение денежных сумм превратить совсем несложно. С произвольными текстовыми полями (например, фамилиями людей) работать нельзя и их нужно сделать незначительными.
Во многих реальных задачах приходится иметь дело с не совсем достоверными данными. Значения некоторых переменных могут быть испорчены шумом или частично отсутствовать. Существуют специальные средства работы с пропущенными значениями (они могут быть заменены на среднее значение этой переменной или на другие ее статистики), так что если данных немного, можно включить в рассмотрение случаи с пропущенными значениями. Нейронные сети в основном стойкие к шумам. Однако у этой стойкости есть граница. Например, выбросы, то есть значения, которые лежат очень далеко от области нормальных значений переменной, могут исказить результат обучения. В таких случаях лучше всего постараться найти и обнаружить эти выбросы (изъять соответствующие примеры или превратить выбросы в пропущенные значения). Если выбросы обнаружить тяжело, то можно воспользоваться возможностями сделать процесс обучения стойким к выбросам, однако такое обучения, как правило, менее эффективно.
Сглаживание данных
Положительный эффект достигается при использовании дополнительной нейросети, функционирующей в режиме сглаживания входных данных обучающего множества. В режиме обучения дополнительной сети каждая реализация обучающего множества приобретает вид: вектор входных значений®вектор входных значений (рис. 3).
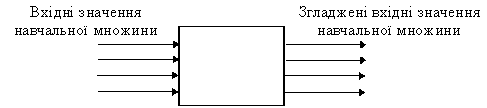
Рис. 3. Пример применения нейросети для сглаживания данных
В режиме функционирования на входы подаются входные значения обучающего множества, на выходе получаем сглаженные значения, без имеющихся выбросов, которые в дальнейшем можно использовать для обработки. Можно дать следующее пояснение эффекта сглаживание данных. Зависимость выходных значений нейросети от входных может быть представлена суммарным степенным полиномом, так как передаточные функции нейронов скрытого слоя - полиномиальные. При незначительном числе нейронов скрытого слоя и невысоких степенях полиномов суммарный полином будет невысокой степени, приводит к сглаживанию.
Вопрос о том, сколько примеров нужно иметь для обучение сети, часто непростой. Известно ряд правил, которые согласовывают число необходимых примеров с размерами сети (простейшее из них говорит, что число примеров должно быть в десять раз больше числа связей в сети). На самом деле, это число зависит также от сложности отображения, которое нейронна сеть стремится воссоздать. С ростом количества параметров количество необходимых примеров растет нелинейно, так что уже при довольно небольшом числе параметров может понадобиться огромное число примеров.
Для большинства реальных задач бывает достаточно нескольких сотен или тысяч примеров. Для сложных задач может понадобиться еще большее количество, однако редко встречается задача, где хватило бы менее сотни примеров. Если данных меньше, то информации для обучение сети недостаточно.
Задачи регрессии
Особое значение имеют задачи предвидения и прогнозирования временных рядов, среди которых выделяются задачи с набором определенных специфических признаков, поэтому следует провести их классификацию. Задачи исследования явлений, развитие которых связано со временем, можно поделить на несколько классов:
По характеру основных признаков объекта:
- прогнозирование явлений, реализации которых представленные
в виде детерминированных временных рядов. Такие задачи, в частности,
можно решить путем применения методов математического анализа;
- прогнозирование явлений, реализации которых представлены в виде
индетерминированных временных рядов. Решение этих задач традиционно
осуществляется путем применения методов теории вероятностей и
математической статистики. В частности, реализации таких явлений,
могут иметь вид:
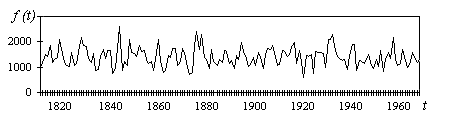
Рис. 4. Розподіл річного стоку Дніпра в часі
б) нестационарного временного ряда, который характеризуется определенной тенденцией развития в времени (рис. 2); при исследовании нестационарных процессов можно выделить участки, на которых процесс можно считать стационарным; выбор промежутка для формирования обучающего множества в таком случае избирается согласно задачи прогнозирования.
На рис. 5 приведены ежедневные нормированные данные микросейсмических колебаний Земли за определенный период времени.
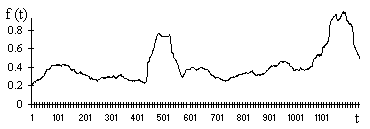
Рис. 5. Распределение микросейсмических колебаний Земли в времени
По числу признаков объекта исследований:
- одномерная задача; явление представлено лишь одним признаком, изменения которого происходят во времени; на рис. 3 изображены данные наблюдений относительных чисел Вольфа, усредненные за месяц, за период с 1900 по 1924 год;
- многомерная задача; объект или явление представлены несколькими признаками (рис. 7); задача прогнозирования может быть расширена благодаря представлению данных в пространстве (рис. 8).
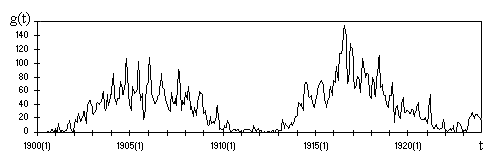
Рис. 6. Распределение чисел Вольфа во времени
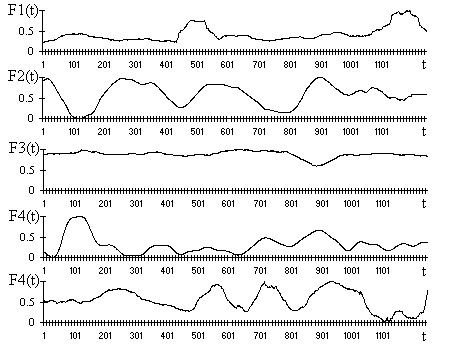
Рис. 7. Основные предвестники сейсмической активности
На рис. 7 представлены ежедневные данные некоторых из основных признаков, определяющих землетрясение. Показанные данные, в частности:
- F1 — акоистика,
- F2 — деформации земной поверхности,
- F3 — микросейсмические колебания Земли,
- F4 — суммарная энергия землетрясения,
- F5 — температура Земли,
В качестве примера многомерной задачи покажем оценивания числа групп солнечных пятен, усредненных за год, которые определяются двумерным распределением в области двух аргументов — широта-время (рис. 8).
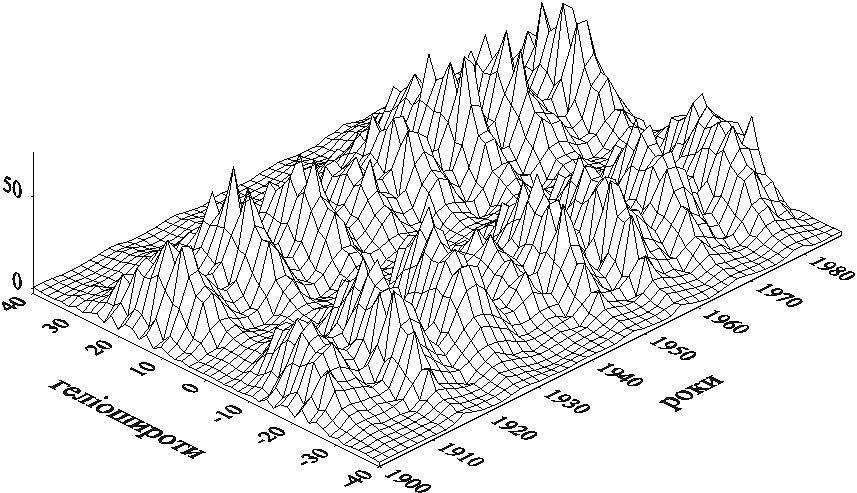
Рис. 8. Пространственное отображение количества солнечных пятен в координатах гелиоширота-время
Учитывая специфический характер прогнозирования временных рядов и определенный разнобой в терминологии, будем придерживаться ряда определений.
Предысторией ряда назовем набор элементов временного ряда, который учитывается для одного шага прогнозирования следующих элементов временного ряда. Одношаговое прогнозирование сводится к задачам отображения в случае, когда значение элементов предыстории могут определять лишь один дискретный отсчет выходных величин. Многошаговое прогнозирование характеризуется увеличением дискретных отсчетов выходной величины и, соответственно, увеличением времени, на который осуществляется прогноз (время опережения Топ). При многошаговом прогнозировании Топ=а*R, где R — количество шагов вычисления прогнозирования; а — шаг дискретизации выходного параметра (например, год, месяц, день, и т.п.).
По времени опережения различают виды прогнозов:
- сглаживание, R= 0;
- краткосрочный прогноз, R= 1 — 2;
- середнесрочный прогноз, R= 3 — 7;
- долгосрочный прогноз, R= 10 — 15.
Адаптация нейросетей в режимах прогнозирования к данным обучающим множествам
Данные про поведение объекта, признаки которого связаны с течением времени, представлены как результаты наблюдений в равномерные отсчеты времени. Для моментов времени t=1, 2, ..., n данные наблюдений приобретают вид временного ряда х(t1), х(t2), ..., х(tn). Информация про значения временного ряда до момента n позволяет давать оценки параметров x(tn+1), x(n+2), ..., x(n+m). Для прогнозирования элементов временных рядов широко используют так называемый метод "временных окон".
В зависимости от количества признаков, представляющих значения рядов при формировании множеств данных, выделим задачи двух типов.
Однопараметрическая задача прогнозирования
Пусть временной ряд x(t) задан отсчетами процесса x(t1), x(t2),..., x(tі) в дискретные моменты времени t. Зададим ширину (количество дискретных отсчетов) входного временного окна m, ширину выходного окна р. Входное и выходное окна накладываются на данные ряда, начиная с первого элемента (рис. 9).
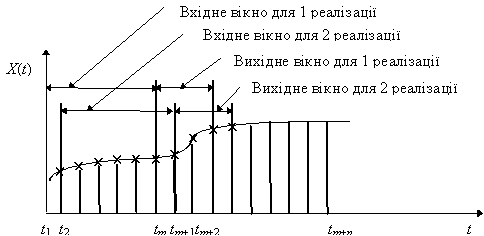
Рис. 9. Формирование множеств данных для однопараметрической задачи прогнозирования по методу "временных окон"
Входное окно формирует данные для входов нейронной сети, а выходное, соответственно, для выходов. Подобная пара входного и выходного векторов принимается за одну реализацию временного ряда. При сдвиге временных окон по временному ряду с шагом s, получаем вторую и следующие реализации.
Значение ширины окон и шага смещения должны согласовываться с особенностями временного ряда, который обеспечивается путем проведения экспериментов. Пусть входное окно имеет ширину m, выходное окно р=1, шаг смещения s=1. Тогда сформированное множество значений для однопараметрической задачи будет иметь вид, приведенный ниже:
Таблица 1.
|
Входы |
Выходы |
|||
| x(t1) | x(t2) | ... | x(tm) | x(tm+1) |
| x(t2) | x(t3) | ... | x(tm+1) | x(tm+2) |
| x(t3) | x(t4) | ... | x(tm+2) | x(tm+3) |
| ... | ... | ... | ... | ... |
| x(tі) | x(tі+1) | ... | x(ti+m-1) | x(ti+m) |
Многопараметрическая задача прогнозирования
В многомерных (многопараметрических) задачах прогнозирования подходы к решению проблемы подобны (рис.10).
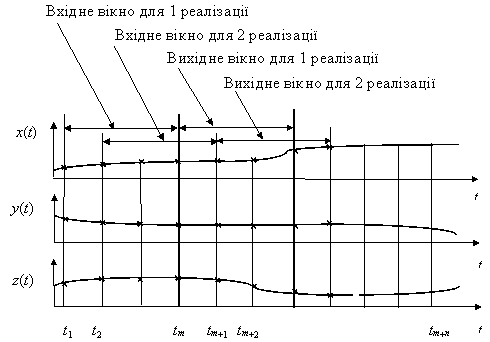
Рис. 10. Формирование множеств данных для многопараметрической задачи
Пусть нужно спрогнозировать взаимозависимые величины x(t), y(t), ..., z(t). Если принять ширину входного окна m, выходного р=1, шага смещения s=1, можно сформировать множество данных следующим образом:
Таблица 2
|
Входы |
||||||||
| x(t1) | x(t2) | x(tm) | y(t1) | y(t2) | y(tm) | z(t1) | z(t2) | z(tm) |
| x(t2) | x(t3) | x(tm+1) | y(t2) | y(t3) | y(tm+1) | z(t2) | z(t3) | z(tm+1) |
| x(t3) | x(t4) | x(tm+2) | y(t3) | y(t4) | y(tm+2) | z(t3) | z(t4) | z(tm+2) |
| x(ti) | x(ti+1) | x(ti+m-1) | y(ti) | y(ti+1) | y(ti+m-1) | z(ti) | z(ti+1) | z(ti+m-1) |
|
Выходы |
|||
| x(tm+1) | y(tm+1) | z(tm+1) | |
| x(tm+2) | y(tm+2) | z(tm+2) | |
| x(tm+3) | y(tm+3) | z(tm+3) | |
| x(ti+m-1) | y(ti+m-1) | z(ti+m-1) | |
Функционирование нейросети осуществляется в соответствии с показанным методом временных окон, сохраняя значения ширины окон и шага смещения.
Конкретизация подходов к реализации прогнозирования в значительной мере зависит от особенностей исследуемого явления.
Одношаговое прогнозирование (предвидение)
Задача одношагового прогнозирования сводится к задаче отображения, когда один входной вектор отображается в выходной (рис. 11).
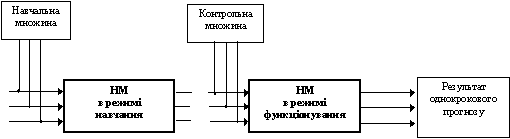
Рис. 11. Последовательность использования нейросети для задач предвидения
В случае однопараметрической задачи предвидения обучающее множество до момента n, при условии m=3, p=1, s=1, будет иметь вид приведеный в табл. 3.
Таблица 3
|
Входы |
Выход |
||
| x(t1) | x(t2) | x(t3) | x(t4) |
| x(t2) | x(t3) | x(t4) | x(t5) |
| ... | ... | ... | ... |
| x(tn-3) | x(tn-2) | x(tn-1) | x(tn) |
В режиме обучения устанавливаются коэффициенты весов связей, после чего становится возможным переход к режиму функционирования. Для предвидения на входы нейросети поступают значения последней реализации обучающего множества x(tn-2), x(tn-1), x(tn). На выходе формируется прогнозируемая величина x*(tn+1).
Для многопараметрической задачи предвидения на входы обученной нейросети подаются векторы x(tn-2), y(tn-2), z(tn-2), x(tn-1), y(tn-1), z(tn-1), x(tn), y(tn), z(tn). На выходы нейросети поступают предвиденные величины x*(tn+1), y*(tn+1), z*(tn+1), которые откладываются в выходной вектор предвиденных данных.
Показанный режим является одношаговым, что работает в режиме отображения (реальный вход®прогнозируемый выход). Предвидение применяют для моделирования дискретных последовательностей, которые не связаны со временем. Учитывая специфику временных рядов, такой тип прогноза не всегда целесообразен, но в определенных случаях краткосрочных прогнозов им можно воспользоваться.
Многошаговое прогнозирование
Многошаговое прогнозирование применяют лишь для явлений, признаки которых представлены в виде временных рядов.
Для однопараметрической задачи прогнозирования обучающее множество будет иметь вид приведенный в табл. 3. Во время обучения сеть настраивает коэффициенты весов связей и полиномов передаточных функций, что в дальнейшем и определяет режим функционирования. Многошаговое прогнозирование временного ряда осуществляется следующим образом (рис. 12). На входы нейросети подается вектор известных значень x(tn-2), x(tn-1), x(tn). На выходе формируется прогнозируемая величина x*(tn+1), которая определяет вектор прогнозируемых выходов и одновременно добавляется к значениям обучающего множества, то есть, принимается как достоверная. Далее на входы подается вектор x(tn-1), x(tn), x*(tn+1), а на выходе получается x*(tn+2) и следующие прогнозируемые значения.
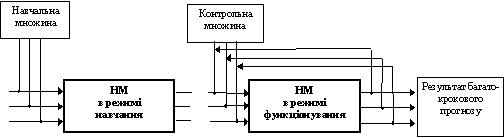
Рис. 12. Последовательность использования нейросетей для задач многошагового прогнозирования
Для многомерной задачи прогнозирования на входы обученной нейросети подаются векторы x(tn-2), y(tn-2), z(tn-2), x(tn-1), y(tn-1), z(tn-1), x(tn), y(tn), z(tn). На выходе продуцируются величины x*(tn+1), y*(tn+1), z*(tn+1), которые формируют вектор выходных значений и последовательно добавляются к значениям обучающего множества. При сдвиге окна на шаг, выходные данные, спродуцированные сетью, воспринимаются как реальные и принимают участие в прогнозировании следующего значения выхода, то есть на входы подаем вектор x(tn-1), y(tn-1), z(tn-1), x(tn), y(tn), z(tn), x*(tn+1), y*(tn+1), z*(tn+1), а на выходе получаем x*(tn+2), y*(tn+2), z*(tn+2) и следующие прогнозируемые значения.
Многошаговое прогнозирование позволяет делать коротко- и среднесрочные прогнозы, поскольку существенное влияние на точность имеет накопление погрешности на каждом шаге прогнозирования. При применении долгосрочного многошагового прогнозирования наблюдается характерное для многих прогнозирующих систем постепенное затухание процесса, фазовые сдвиги и другие искажения картины прогноза. Такой тип прогнозирования подходит для стационарных временных рядов с небольшой случайной составляющей.
Многошаговое прогнозирование с переобучением нейросети на каждом шаге прогноза
Быстрые неитерационные алгоритмы обучения позволяют предложить новый тип многошагового прогноза, который может быть применен при долгосрочных прогнозах с сохранением удовлетворительной точности прогнозирования.
Аналогично с предыдущим алгоритмом прогнозирования на входы сети в режиме функционирования поступает последняя реализация обучающего множества x(tn-2), x(tn-1), x(tn). Прогнозируемое значение выхода x*(tn+1) откладывается в векторе прогнозируемых выходных значений и в качестве достоверного прибавляется к реальным значениям обучающего множества. Обучающее множество увеличивается на одно временное окно. Происходит процесс переобучения сети на увеличенном обучающем множестве, во время которого определяются новые весовые коэффициенты k синаптических связей и полиномов передаточных функций нейронов (рис. 13).
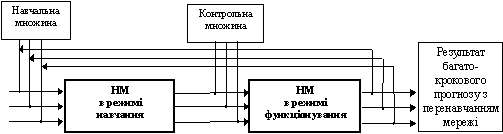
Рис. 13. Последовательность использования нейросети для задач многошагового прогнозирования с переобучением
Реализация x(tn-1), x(tn), x*(tn+1), как значение следующего входного окна подается на входы сети в режиме функционирования. Сеть продуцирует новое выходное значение x*(tn+2), которое также откладывается в вектор спродуцированных выходов и добавляется к реальным значениям обучающего множества, с целью дальнейшего переобучения сети и установления возобновленных коэффициентов полиномов передаточных функций и синаптических связей. Итерационная процедура переобучения распространяется к прогнозируемому значению x*(tN).
Такой подход позволяет при больших интервалах опережения устранить затухание прогностических свойств сети за счет постоянного корректирования весовых коэффициентов синаптических связей.
Отметим, что алгоритм многошагового прогнозирования с переобучением сети для традиционных сетей прямого распространения с итерационным обучением является практически невыполнимым через большие временные задержки, необходимые на перенастраивание коэффициентов сети.
Критерии оценки качества функционирования сети
Критерии оценки можно поделить на внутренние и внешние. Внутренние критерии формируются на основе информации множества данных, использованного для обучения, тогда как внешние критерии используют новую информацию тестового множества, элементы которых не использовались при обучении. Оптимальная сложность модели сети устанавливается на основе внешних и внутренних критериев.
К внешним критериям выбора модели можно отнести:
Критерий регулярности — внешний критерий, для вычисления величины которого требуется тестовое множество данных.
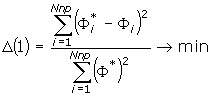
где D (1) — величина критерия; і — номер выхода; Fі — значения выходов сети; Fі* — точные значения выходов.
Физический смысл применения критерия регулярности состоит в выборе модели, которая будет максимально точной на элементах тестового множества, невходящего в состав обучающего множества.
Критерий минимального смещения требует максимального совпадения значений выходной величины для двух моделей, где в качестве обучающих примеров были использованы данные разных подмножеств обучающего множества.
Критерий минимального смещения позволяет выбрать модель, которая "слабо реагирует" на смену обучающего множества и зашумленные тестовые данные.
Критерий смещенности показателей во времени — помогает оценить уровень взаимосвязи переменных. Отдельные показатели могут иметь разное последействие, поэтому раздельное прогнозирование каждого из них может обеспечить лучший результат. Соответственно, при наличии тесной взаимосвязи между показателями, прогнозирование их совокупности улучшает результаты прогноза каждого из них. Возможное также включение нового параметра, который может быть или дополнительным признаком или линейной комбинацией уже имеющихся признаков. Применение этого критерия помогает в оптимальном подборе признаков явления, которые обеспечивают высокую точность прогнозирования.
Критерий физической достоверности — требует исключение моделей, которые во время проведения эксперимента, могут продуцировать нереальные результаты (большие выбросы для прогнозируемого множества).
Оценивание точности прогнозов
Как правило, после обучения нейросети осуществляют контрольное воспроизведение данных, составляющих обучающее множество. Если точность воспроизведения удовлетворительная и отклонение находятся в допустимых границах, считают, что построена удовлетворительная модель и следует ожидать достаточное качество отображения. Если при воспроизведении сетью данных обучающего множества наблюдаются большие расхождения, можно предположить что это вызвано:
- наличием неточных данных с большой случайной составляющей. Для устранения этого повышают требования к точности измерений; в случае временного ряда, возможно уменьшение шага дискретизации, например использование ежемесячных значений вместо годовых;
- неучтенными признаками, которые в значительной мере определяют закономерность; эта проблема может быть решена расширением набора признаков, принимаемых во внимание.