Квантовый компьютер
Пехотин Е.В.
Источник: Обзорный курсовой доклад по курсу «Информационные Системы»
Рисунок 1 показывает приблизительно в натуральную величину часть картины тени, отбрасываемой светонепроницаемой перегородкой с двумя прямыми параллельными щелями, находящейся на расстоянии трех метров от экрана. Щели находятся на расстоянии одной пятой миллиметра друг от друга и освещаются прямым красным лучом лазера расположенного по другую сторону перегородки.

Рисунок 1 – Базовая интерференционная светотеневая картина 2 прямых параллельных интерференционных щелей
Если бы свет распространялся прямолинейно, картина, изображенная на рисунке, представляла бы две ярких полосы с резкими границами, расположенные на расстоянии одной пятой миллиметра друг от друга (что было бы невозможно увидеть при таком масштабе), а остальная часть экрана осталась бы в тени. Но в действительности свет искривляется так, что образует много ярких и темных полос без резких границ. Если увеличить расстояние между щелями так, чтобы они оставались в пределах лазерного луча, расстояние между полосами на экране увеличится на столько же. В этом отношении тень ведет себя как обычная тень, отбрасываемая крупным предметом. А какую тень мы получим, если прорежем в перегородке между двумя существующими щелями еще две идентичные щели, так, что у нас будет четыре щели, расположенные на расстоянии одной десятой миллиметра друг от друга? Можно ожидать, что картина, изображенная на рисунке 1, останется практически неизменной. Как-никак первая пара щелей отбрасывает тени, показанные на рисунке 1, и, как я уже сказал, вторая пара щелей должна произвести подобную картину тени, сдвинутую в сторону на одну десятую миллиметра – почти на том же самом месте. Кроме того, мы знаем, что лучи света пересекаются, не оказывая никакого воздействия друг на друга. Так что две пары щелей должны дать ту же самую картину тени, но в два раза ярче и чуть более размытую.
В действительности происходит нечто отличное. Действительная тень, отбрасываемая перегородкой с четырьмя прямыми параллельными щелями, показана на рисунке 2. Ясно, что тень от четырех щелей представляет собой отнюдь не комбинацию двух слегка отдаленных друг от друга теней от двух щелей, а имеет новую и более сложную картину. В этой картине есть такие участки, как точка X. которая не освещена на картине тени от четырех щелей и освещена на картине тени от двух щелей. Эти участки освещались при наличии в перегородке двух щелей, но перестали освещаться, когда в перегородке прорезали еще две щели, пропускающие свет. Появление этих щелей воспрепятствовало попаданию света в точку X.

Рисунок 2 – Интерференционная светотеневая картина 4 прямых параллельных интерференционных щелей
Таким образом, появление еще двух источников света затемняет точку X. а их удаление снова освещает ее. Каким образом? Можно представить два фотона, направляющиеся к точке Х и отскакивающие друг от друга как бильярдные шары. Только один из фотонов мог бы попасть в точку X, но они мешали друг другу, и потому ни один из них туда не попал. Скоро я покажу, что это объяснение не может быть истинным. Тем не менее, основной идеи избежать невозможно: через вторую па¬ру щелей должно проходить что-то, препятствующее попаданию света из первой пары щелей в точку X. Но что? Это мы можем выяснить с помощью дальнейших экспериментов.
Что нам ожидать при проведении этих экспериментов только с одним фотоном? Например, предположим, что наш фонарик расположен так далеко от экрана, что за целый день на экран попадает только один фотон. Что увидит наша лягушка, наблюдающая за экраном? Если то, что каждому фотону мешают другие фотоны, – правда, то не уменьшится ли интерференция, когда фотоны будут появляться реже? Не прекратится ли она вовсе, если через аппарат за раз будет проходить только один фотон? Мы по-прежнему можем ожидать появления полутеней, т. к. фотон при прохождении через щель может отклониться от своего курса (например, ударившись о край щели). Но на экране мы точно не должны увидеть участок, подобный точке X, который получает фотоны, когда открыты две щели, и становится темным когда открывают две другие.
Однако именно это мы и наблюдаем. Независимо от того, насколько редко появляются фотоны, картина тени остается неизменной. Даже при проведении эксперимента с появлением одного фотона за раз этот фотон не попадает в точку X. когда открыты все четыре щели. Но стоит только закрыть две щели, и вспышки в точке Х возобновляются.
Возможно ли, чтобы фотон расщеплялся на фрагменты, которые после прохождения через щели изменяли бы свою траекторию и рекомбинировались? Эту возможность мы тоже можем исключить. Если снова выпустить из аппарата один фотон и у каждой щели установить по детектору, то зарегистрировать сигнал сможет максимум один из них. Поскольку при подобном эксперименте никогда не наблюдались сигналы на двух детекторах одновременно, можно сказать, что обнаруживаемые ими объекты не расщепляются.
Таким образом, если фотоны не расщепляются на фрагменты и отклоняются от траектории не под действием других фотонов, то что же вызывает это отклонение? Когда через аппарат проходит один фотон за раз, что может проходить через другие щели, чтобы помешать ему?
Давайте подойдем к рассмотрению этого вопроса критически. Мы обнаружили, что когда один фотон проходит через этот аппарат,
- он проходит через одну щель, затем что-то воздействует на него, заставляя отклониться от своей траектории, и это воздействие зависит от того, какие еще щели открыты;
- воздействующие объекты прошли через другие щели;
- воздействующие объекты ведут себя так же, как фотоны ...
- ... но они невидимы.
С этого момента я буду называть воздействующие объекты «фотонами». Именно фотонами они и являются, хотя на данный момент представляется, что существует два вида фотонов, один из которых я временно назову реальными фотонами, а другой теневыми фотонами. Первые мы можем увидеть или обнаружить с помощью приборов, тогда как вторые – неосязаемы (невидимы): их можно обнаружить только косвенно через их воздействие на видимые фотоны. Каждый реальный фотон находится под сопровождением эскорта теневых фотонов и что при прохождении фотона через одну из четырех щелей некоторые теневые фотоны проходят через три оставшиеся. Поскольку при изменении положения щелей (при условии, что они находятся в пределах луча) на экране появляются различные интерференционные картины, теневые фотоны должны попадать на всю освещенную часть экрана, куда попадает реальный фотон. Следовательно, теневых фотонов гораздо больше, чем реальных. Сколько же их? Эксперименты не могут определить верхнюю границу этого числа, но устанавливают приблизительную нижнюю границу. Максимальная площадь, которую освещали с помощью лазера в лаборатории, составила около квадратного метра, а минимальный достижимый размер отверстий мог быть около одной тысячной миллиметра. Таким образом, возможно получить около 1012 (одного триллиона) положений отверстий на экране. Следовательно, каждый реальный фотон должен сопровождать, по крайней мере, триллион теневых.
Таким образом, мы узнали о существовании бурлящего, непомерно сложного скрытого мира теневых фотонов. Они распространяются со скоростью света, отскакивают от зеркал, преломляются линзами и останавливаются, встретив светонепроницаемые барьеры или фильтры другого цвета. Однако они не оказывают никакого воздействия даже на самые чувствительные детекторы. Единственная вещь во вселенной, через которую можно наблюдать теневой фотон, – это воздействие, которое он оказывает на реальный фотон, им сопровождаемый. В этом и заключается явление интерференции. Если бы не это явление и не странные картины теней, которые мы наблюдаем, теневые фотоны были бы абсолютно незаметными.
Интерференция свойственна не только фотонам. Квантовая теория предсказывает, а эксперимент подтверждает, что интерференция происходит с любой частицей. Так что каждый реальный нейтрон должны сопровождать массы теневых нейтронов, каждый электрон – массы теневых электронов и т. д. Каждую из этих теневых частиц можно обнаружить лишь косвенно через ее воздействие на движение реального двойника.
Реальные частицы обладают свойством, которое дает нам право называть их совокупность Вселенной. Это определяющее свойство заключается просто в их реальности, то есть во взаимодействии друг с другом и, следовательно, в том, что их можно непосредственно обнаружить с помощью приборов и чувствительных датчиков, созданных из других реальных частиц. По тем же причинам мы могли бы назвать совокупность теневых частиц параллельной Вселенной, ибо теневые частицы оказываются под воздействием реальных частиц только через явление интерференции. Но мы можем сделать еще лучше. Оказывается, что теневые частицы разделяются между собой точно так же, как отделяется от них вселенная реальных частиц. Другими словами, они образуют не одну однородную параллельную вселенную, гораздо большую, чем реальная, а огромное количество параллельных вселенных, каждая из которых по составу похожа на реальную и подчиняется тем же законам физики, но отличается от других расположением частиц.
Замечание относительно терминологии. Слово «вселенная» традиционно использовали для обозначения «всей физической реальности». В этом смысле может существовать не более одной вселенной. Для обозначения же физической реальности в целом создали неологизм – мультиверс (а вселенная – это универс).
Опыты с интерференцией одной частицы, подобные описанным мной, показывают, что мультиверс существует и содержит множество двойников каждой частицы реальной вселенной. Чтобы прийти к следующему выводу о разделении мультиверса на параллельные вселенные, следует рассмотреть явление интерференции нескольких реальных частиц. Самый простой способ осуществить это – спросить при «мысленном эксперименте», что должно происходить на микроскопическом уровне, когда теневые фотоны встречают светонепроницаемый объект. Безусловно, они останавливаются: мы знаем это, поскольку интерференция прекращается, когда на пути теневых фотонов появляется светонепроницаемая перегородка. Но почему? Что их останавливает? Мы можем исключить прямой ответ, что реальные атомы перегородки поглощают их так же, как поглотили бы реальные фотоны. Одно нам известно: теневые фотоны не взаимодействуют с реальными атомами. Кроме того, мы можем проверить, заменив перегородку детектором, что атомы не поглощают энергию и не изменяют свое состояние до тех пор, пока не встретят реальный фотон. Теневые фотоны не оказывают на них никакого влияния.
Другими словами, перегородка одинаково воздействует, как на реальные, так и на теневые фотоны, но теневые фотоны вообще не оказывают на нее никакого воздействия. Это и является определяющим свойством теневых фотонов, поскольку, если бы они оказывали реальное воздействие хоть на какой-то материал, то этот материал можно было бы использовать как детектор теневых фотонов, а само явление теней и интерференции не существовало бы в том виде, в каком оно здесь описан.
Следовательно, в месте существования реальной перегородки находится и теневая. Без особых усилий можно сделать вывод, что эта теневая перегородка состоит из теневых атомов, которые, как нам уже известно, должны присутствовать как двойники реальных атомов перегородки. У каждого реального атома существует множество двойников. Каждый теневой фотон встречает перегородку, во многом подобную той, которую встречает его реальный двойник, перегородку, состоящую из крошечного количества существующих теневых атомов.
По той же причине каждый теневой атом в перегородке может взаимодействовать лишь с небольшим количеством других теневых атомов, находящихся около него, и те, с которыми он взаимодействует, образуют перегородку, весьма похожую на реальную. И так далее. Вся материя и все физические процессы имеют такую структуру. Другими словами, частицы группируются в параллельные вселенные. Они «параллельны» в том смысле, что в пределах каждой вселенной частицы взаимодействуют друг с другом так же, как в реальной вселенной, но воздействие, оказываемое каждой вселенной на остальные, весьма слабое, и проявляется оно через явление интерференции.
Таким образом, мы вывели цепочку умозаключений, которая начинается со странных картин тени и заканчивается параллельными вселенными. На каждом этапе мы обнаруживаем, что поведение наблюдаемых нами объектов можно объяснить только присутствием невидимых объектов и их определенными свойствами. Основная идея заключается в том, что интерференция одной частицы определенно исключает возможность существования только реальной вселенной, которая нас окружает. А факт существования такого явления интерференции неоспорим.
Квантовый компьютер – это машина, использующая уникальные квантово-механические эффекты, в особенности, интерференцию, для выполнения совершенно новых видов вычислений, которые, даже в принципе, невозможно выполнить ни на одной машине Тьюринга, а следовательно, ни на каком классическом компьютере. Таким образом, квантовое вычисление – это принципиально новый способ использования природы.
Квантовое вычисление, которое сейчас находится в зачаточном состоянии, – качественно новый этап этого движения. Это будет первая технология, которая позволит выполнять полезные задачи при участии параллельных вселенных. Квантовый компьютер сможет распределить составляющие сложной задачи между множеством параллельных вселенных, а затем поделиться результатами.
Рассмотрим задачу умножения двух достаточно больших чисел, скажем.
При умножении семизначных чисел общее время, необходимое для умножения, будет равно семи, умноженному на семь, или 49 микросекундам. При введении чисел, примерно в десять раз больших, содержащих по восемь цифр, время, необходимое для их умножения, будет равно 64 микросекундам: увеличение составляет всего 31%.
Напротив, разложение на множители, по сути процесс, обратный умножению, кажется гораздо сложнее. В начале вводится одно число, скажем, 10949769651859, задача заключается в том, чтобы найти два множителя, меньших числа, произведение которых равно 10949769651859. Поскольку мы только что умножили эти числа, мы знаем, что в этом случае ответ будет 4220851 и 2594209. Но не обладая таким внутренним знанием, как мы нашли бы эти множители?
Самый очевидный метод разложения на множители – делить вводимое число на все возможные множители, начиная с 2 и продолжая каждым нечетным числом, до тех пор, пока введенное число не разделится без остатка. По крайней мере, один из множителей не может быть больше квадратного корня введенного числа, что позволяет оценить, сколько времени может занять этот метод. В рассматриваемом нами случае наш компьютер найдет меньший из двух множителей,
Этот метод можно усовершенствовать, однако всем современным методам разложения числа на множители присуще это свойство экспоненциального увеличения. Самое большое число, которое было «в гневе» разложено на множители, имело 129 разрядов. Разложение на множители выполнили с помощью сети Интернет глобальными совместными усилиями, задействовав тысячи компьютеров. Дональд Кнут подсчитал, что разложение на множители 250-значного числа при использовании самых эффективных из известных методов, с помощью сети, состоящей из миллиона компьютеров, заняло бы более миллиона лет. Никто не может даже представить себе, как можно разложить на множители числа, состоящие из тысячи или миллиона разрядов. По крайней мере, этого никто не мог представить до недавнего времени.
Квантовую теорию часто представляют как теорию, которая делает только вероятностные предсказания. Например, в эксперименте по интерференции со светонепроницаемой перегородкой со щелями можно видеть, что фотон попадает в любое место на «светлом» участке картины теней. Однако важно понимать, что для множества других экспериментов квантовая теория предсказывает единственный определенный результат. Другими словами, она предсказывает, что все вселенные окончатся с одним и тем же результатом, даже если на промежуточных стадиях эксперимента эти вселенные отличались друг от друга, и она предсказывает, каким будет этот результат. В таких случаях мы наблюдаем неслучайное явление интерференции. Такие явления может продемонстрировать интерферометр. Это оптический инструмент, состоящий главным образом из зеркал, как обычных, так и полупрозрачных. Если фотон ударяется о полупрозрачное зеркало, то в половине вселенных он отскакивает от него точно так же, как отскочил бы от обычного зеркала. Однако в другой половине вселенных он проходит сквозь это зеркало, словно его нет.
Один фотон входит в интерферометр сверху слева, как показано на рисунке 3. Во всех вселенных, где проводят эксперимент, фотон и его двойники движутся к интерферометру по одной и той же траектории. Следовательно, эти вселенные идентичны. Но как только фотон ударяется о полупрозрачное зеркало, первоначально идентичные вселенные становятся различными. В половине из них фотон проходит через это зеркало и перемещается вдоль верхней стороны интерферометра. В остальных вселенных фотон отскакивает от зеркала и перемещается вдоль левой стороны интерферометра. Затем разновидности фотона в этих группах вселенных ударяются об обычные зеркала справа сверху и слева снизу соответственно и отскакивают от них. Таким образом, в конце они одновременно попадают на полупрозрачное зеркало справа снизу и интерферируют друг с другом. Не забывайте, что мы пускали в аппарат только один фотон, и в каждой вселенной по-прежнему находится только один фотон. Во всех вселенных этот фотон теперь ударился о правое нижнее зеркало. В половине вселенных он ударился об это зеркало слева, в другой половине – сверху. Между разновидностями фотона из этих двух групп вселенных произошла сильная интерференция. Суммарный эффект зависит от точной геометрии ситуации, но на рисунке изображен тот случай, когда во всех вселенных фотон в конце движется вправо сквозь зеркало, и ни в одной вселенной он не передается или не отражается вниз. Таким образом, в конце эксперимента все вселенные так же идентичны, как и в начале. Они отличались и взаимодействовали друг с другом всего лишь долю минуты в промежуточном состоянии.
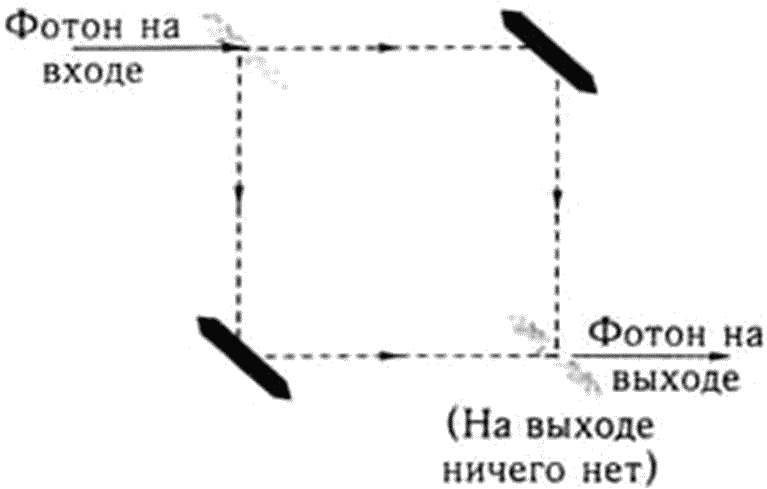
Рисунок 3 – Демонстрация квантового эффекта на интерферометре
Идея квантовых вычислений, впервые высказанная Ю. И. Маниным и Р. Фейнманом, состоит в том, что квантовая система из L двухуровневых квантовых элементов (квантовых битов, кубитов) имеет 2L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, пространством состояний такого квантового регистра является 2L-мерное гильбертово пространство. Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит может выполнять параллельно 2L операций.
Предположим, что имеется один кубит. В таком случае после измерения, в так называемой классической форме, результат будет 0 или 1. В действительности кубит – квантовый объект и поэтому, вследствие принципа неопределённости, в результате измерения может быть и 0, и 1 с определенной вероятностью. Если кубит равен 0 (или 1) со стопроцентной вероятностью, его состояние обозначается с помощью символа |0〉 (или |1〉) – в обозначениях Дирака. |0〉 и |1〉 – это базовые состояния. В общем случае квантовое состояние кубита находится «между» базовыми и записывается, в виде
Пример: имеется кубит в квантовом состоянии
- 0 составляет (4/5)² = 16/25 = 64 %;
- 1 составляет (−3/5)² = 9/25 = 36 %.
В данном случае, при измерении мы получили 0 с 64 % вероятностью. Тогда кубит перескакивает в новое квантовое состояние 1*|0〉+0*|1〉=|0〉, то есть, при следующем измерении этого кубита мы получим 0 со стопроцентной вероятностью.
Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: |00〉, |01〉, |10〉 и |11〉. И наконец, общее квантовое состояние системы имеет вид a\,|00〉 + b\,|01〉 + c\,|10〉 + d\,|11〉. Теперь |a|² – вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.
В общем случае системы из L кубитов, у неё 2L классических состояний (00000…(L-нулей), …00001(L-цифр), … , 11111…(L-единиц)), каждое из которых может быть измерено с вероятностями 0–100 %.
Таким образом, одна операция над группой кубитов затрагивает все значения, которые она может принимать, в отличие от классического бита. Это и обеспечивает беспрецедентный параллелизм вычислений.
Упрощённая схема вычисления на квантовом компьютере выглядит так: берется система кубитов, на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством базовых квантовых операций. В конце измеряется значение, и это результат работы компьютера.
Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система дает результат, только с некоторой вероятностью являющийся правильным. Но за счет небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице. С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней.
Чем же квантовый компьютер лучше классического? Большая часть современных ЭВМ работают по такой же схеме: n бит памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически (квантовый) алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов.
Алгоритмы:
- Алгоритм Гровера позволяет найти решение уравнения f(x)=1, 0 ≤ x < N за время O(√N);
- Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время;
- Алгоритм Дойча-Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (
f3(0) = 0 ,f3(1) = 1 ;f4(0) = 1 ,f4(1) = 0 ).
Было показано, что не для всякого алгоритма возможно «квантовое ускорение».
Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма RSA. До сих пор этот алгоритм считается сравнительно надёжным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Для того, например, чтобы получить доступ к кредитной карте, нужно разложить на два простых множителя число длиной в сотни цифр. Даже для самых быстрых современных компьютеров выполнение этой задачи заняло больше бы времени, чем возраст Вселенной, в сотни раз. При помощи алгоритма Шора эта задача делается вполне осуществимой, если квантовый компьютер будет построен.
Применение идей квантовой механики уже открыли новую эпоху в области криптографии, так как методы квантовой криптографии открывают новые возможности в области передачи сообщений. Прототипы систем подобного рода находятся на стадии разработки.
В 1989 году в Нью-Йорке, в Исследовательском Центре IBM, в офисе теоретика Чарльза Беннетта был построен первый рабочий квантовый компьютер. Это был специализированный квантовый компьютер, состоящий из двух квантовых криптографических устройств, спроектированных Беннеттом и Жилем Брассаром из Монреальского Университета. Этот компьютер стал первой машиной, выполнившей небанальные вычисления, которые не смогла бы выполнить ни одна машина Тьюринга.
В квантовой криптосистеме Беннета и Брассара послания кодируются состояниями отдельных фотонов, испускаемых лазером. Несмотря на то, что для передачи сообщения необходимо много фотонов (один фотон на бит, плюс те фотоны, которые тратятся на всевозможные неэффективности), такие машины можно построить, используя существующую технологию, потому что для выполнения своих квантовых вычислений им необходим один фотон на раз. Секретность системы основана не на трудности обработки, как классической, так и квантовой, а непосредственно на свойствах квантовой интерференции: именно она дает этой системе абсолютную секретность, которую невозможно обеспечить с помощью классических методов. Никакой объем будущих вычислений ни на каком компьютере через миллионы или триллионы лет не поможет тому, кто хотел бы подслушать послания, закодированные квантовым методом: поскольку, если кто-либо общается через среду, демонстрирующую интерференцию, то он сможет обнаружить подслушивающих его людей. В соответствии с классической физикой нет ничего, что может помешать подслушивающему, который имеет физический доступ к среде связи, например, к телефонной линии, путем установки пассивного подслушивающего устройства. Но как я уже объяснил, если кто-либо осуществляет какое-либо измерение квантовой системы, он изменяет ее последующие интерференционные свойства. От этого эффекта зависит протокол связи. Связывающиеся стороны эффективно ставят повторяющиеся эксперименты по интерференции, согласуя их через общественный канал связи. Только когда интерференция пройдет проверку на отсутствие подслушивающих, они переходят к следующей стадии протокола, состоящей в том, чтобы использовать некоторую часть переданной информации в качестве криптографического ключа. В худшем случае упорный подслушивающий может помешать связи состояться (хотя, безусловно, этого проще достичь, перерезав телефонную линию). Но что касается чтения сообщения, это может сделать только получатель, для которого оно предназначено, это гарантируют законы физики.
Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит (устройство получило название Orion). Однако информация об этом устройстве не отвечала строгим требованиям точного научного сообщения; новость не получила научного признания. Более того, дальнейшие планы компании (создать уже в ближайшем будущем 1024-кубитный компьютер) вызвали скепсис у членов экспертного сообщества.
В ноябре 2007 года та же компания D-Wave продемонстрировала работу образца 28-кубитного компьютера онлайн на конференции, посвященной суперкомпьютерам. Данная демонстрация также вызвала определенного рода скепсис.
В декабре 2008 года компания организовала проект распределенных вычислений AQUA@home (Adiabatic QUantum Algorithms), в котором тестируются алгоритмы, оптимизирующие вычисления на адиабатических сверхпроводящих квантовых компьютерах D-Wave.
Литература
- Дойч Д. Структура реальности. Перевод с английского Н.А. Зубченко. – РХД, Москва-Ижевск, 2001
- Электронная статья. Квантовый компьютер [Электронный ресурс]: ru.wikipedia.org/wiki/Квантовый_компьютер
