Авторы: Есаян А.Р.
Задача коммивояжера. Варианты решения
Источник статьи:Ссылка
Рассмотрим такую задачу. Коммивояжер (агент по сбыту), отправляясь из своего населенного пункта, должен кратчайшим маршрутом ровно по одному разу посетить n-1 других населенных пунктов и вернуться назад. Это оптимизационная задача, и её различные модификации возникают не только при доставке товаров на дом, но и в ситуациях иного характера. Математические модели задачи коммивояжера содержат большое количество переменных и ограничений. Поэтому для их решения общие методы линейного программирования обычно не используются. Для небольших значений n мы попробуем справиться с задачей коммивояжера, используя рекурсию и метод перебора с возвратом.
Задача 7. Один маршрут коммивояжера. Пусть имеется n пунктов, пронумерованных числами 0,1,…,n-1, и задана матрица U = (Ui,j) (i,j = 0,1,…,n-1), где Ui,j - расстояние между i и j. Написать рекурсивную программу-функцию нахождения одного решения задачи коммивояжера методом перебора с возвратом, если вояж начинается из пункта с номером kÎ{0,1,…,n}.
Решение. Пусть матрица расстояний U определена вне программы, то есть искомые функции могут рассматривать её как глобальный параметр. Числа Ui,j и Uj,i, вообще говоря, не обязательно должны совпадать. При отсутствии дороги между пунктами i и j будем считать, что она есть, но бесконечной длины: Ui,j=¥.
Решением задачи могут служить пара функций commi(n, ne, po, ot, j) и macom(n, k):
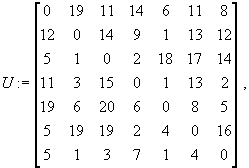
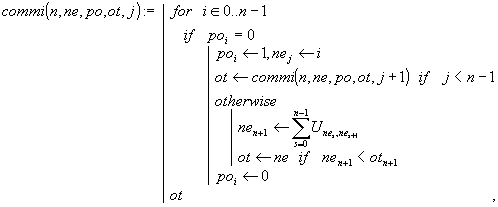
![]()
Головная функция macom(n, k) по заданному количеству пунктов n и номеру пункта отправления k подготавливает фактические аргументы для рекурсивной функции commi():
-
ne = (k, 0 ,…, 0, k, 0) - вектор длины n+2 для формирования маршрута и соответствующего ему расстояния;
-
po - нулевой вектор меток длины n для указания уже пройденных пунктов в формируемом маршруте;
-
ot = (0, 0, …, 0, ¥ ) - вектор длины n+2 для запоминания кратчайшего на текущий момент маршрута и соответствующего ему расстояния;
-
j = 0 - номер рекурсивного вызова.
-
n - количество пунктов;
-
ne = (k, ne1, ..., nen-1, k, nen+1)T - вектор, в котором последовательно формируется очередной маршрут: k®ne1®...®nen-1®k, а затем вычисляется его длина nen+1;
-
po - вектор меток. Если пункт i в j-м рекурсивном вызове подключается к формируемому маршруту (nej¬i), то в векторе меток этот факт фиксируется следующим образом: poi¬1. При переходе к предыдущему рекурсивному уровню или завершению построения одного из возможных путей последний пункт из маршрута удаляется: poi=0;
-
ot - вектор, в котором при otn+1>nen+1 запоминаются очередной найденный маршрут и соответствующее ему расстояние: ot¬ ne;
-
j - уровень рекурсивного вызова.
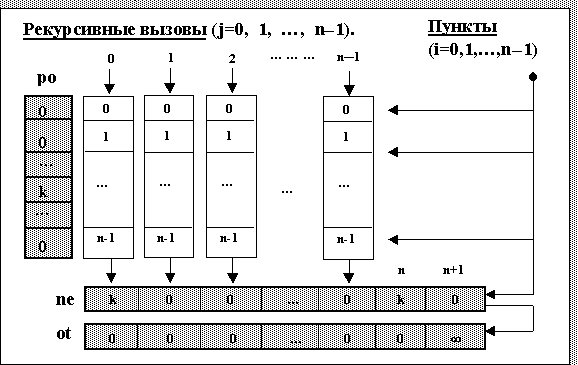
Остановимся подробнее на алгоритме, реализуемом функцией commi(), и динамике формирования текущего маршрута ne. Прежде всего отметим, что рекурсия организована по j - порядковому номеру (от нуля и далее) подключаемого к маршруту пункта (см. рис.6). Пусть мы находимся в j-м рекурсивном вызове, то есть уже сформирован путь k®ne0®...®nej-1. В каждом вызове глубины j делается попытка нарастить текущий путь за счет i-го пункта (i, j = 0, 1, …, n-1), а сам вызов соответствует переходу от работы с текущим пунктом к работе со следующим пунктом. При этом в начале вычислений и при переходах к любому последующему рекурсивному вызову параметр i меняется от нуля и далее с шагом, равным единице, пытаясь принять значение наименьшего номера пункта, допустимого для наращивания пути. При переходах к любому предыдущему рекурсивному вызову параметр i продолжает изменяться от своего текущего на данном уровне значения с шагом, равным единице, также пытаясь принять значение наименьшего номера пункта, допустимого для наращивания пути. Если в текущем рекурсивном вызове путь нарастить уже нельзя, то создавшуюся ситуацию (отрезок сформированного пути) назовем тупиком. Попадание в тупик приводит к завершению текущего рекурсивного вызова, то есть к возврату к предыдущему пункту и продолжению работы с ним. Иных случаев завершения рекурсивных вызовов не существует. Поэтому базой рекурсии мы должны считать совокупность всех тупиков. Заметим, что в данном случае элементы базы заранее, до вычислений, неизвестны.
После наращивания пути в последнем рекурсивном вызове (j = n-1) завершается формирование одного из возможных маршрутов. Для него с помощью матрицы расстояний подсчитывается длина пути. Если она оказывается меньше длины ранее запомненного маршрута (otn+1>nen+1), то в векторе ot запоминается последний маршрут и его длина (ot¬ne). Затем вычисления продолжаются в текущем рекурсивном вызове и т.д., пока мы не попадаем в тупик при работе с начальным пунктом k. Здесь вычисления прекращаются и решение задачи возвращается в виде вектора ot, у которого первые n+1 компонентов задают маршрут, а последний компонент - его длину.
Контрольный пример. Пусть рассматривается матрица расстояний U, приведенная перед функцией commi(). Найти одно из решений задачи коммивояжера для начального пункта 0 можно так:
macom(U,0)T = [0 2 1 4 3 6 5 0 30].
Первые восемь компонентов полученного вектора определяют маршрут коммивояжера: 0®2®1®4®3®6®5®0, а последняя компонента равна длине этого маршрута.
Замечание. Некоторого улучшения быстродействия можно добиться незначительной модификацией функции commi(), если одновременно с наращиванием пути подсчитывать и его текущую длину. Именно так и устроены функции commi1() и macom1():
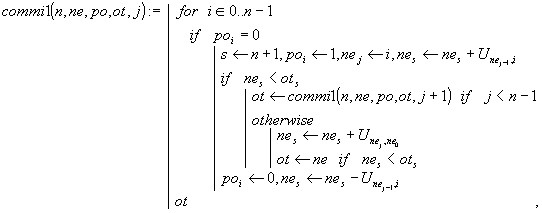
![]()
Задача
8. Все маршруты коммивояжера. Пусть
имеется n пунктов,
пронумерованных числами
0,1,…,n-1, и задана матрица U = (Ui,j) (i,j = 0,1,…,n-1),
где Ui,j - расстояние между i
и j. Написать
рекурсивную программу-функцию нахождения
всех возможных решений задачи коммивояжера
методом перебора с возвратом, если вояж
начинается из пункта с номером kÎ{0,1,…,n}.
Решение. Функции commi2() и macom2() решают поставленную задачу. Их отличие от функций commi1() и macom1() состоит в следующем. Параметр ot здесь не вектор, а построчно наращиваемая матрица. К первому найденному маршруту (нулевая строка ot) в виде последующих строк подсоединяются все другие маршруты с той же самой длиной пути. Если найден маршрут с более коротким путем, то матрица ot начинает формироваться заново. Рекурсия в commi2() и commi1() устроена совершенно одинаково.
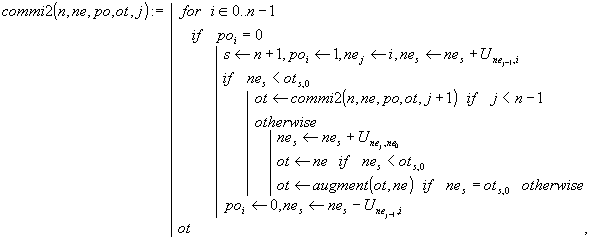
![]()
Контрольный пример. Пусть рассматривается матрица расстояний U, приведенная перед функцией commi(). Найти все решения задачи коммивояжера для начального пункта 0 можно так:

Каждое
из пяти решений занимает в полученной
матрице одну строку, в которой первые
восемь элементов маршруты коммивояжера. Пусть
имеется n пунктов,
пронумерованных числами
0,1,…,n-1, и задана матрица U = (Ui,j) (i,j = 0,1,…,n-1),
где Ui,j - расстояние между i
и j. Написать
рекурсивную программу-функцию нахождения
всех возможных решений задачи коммивояжера
методом перебора с возвратом, если вояж
начинается из пункта с номером kÎ{0,1,…,n}.
Решение. Функции commi2() и macom2() решают поставленную задачу. Их отличие от функций commi1() и macom1() состоит в следующем. Параметр ot здесь не вектор, а построчно наращиваемая матрица. К первому найденному маршруту (нулевая строка ot) в виде последующих строк подсоединяются все другие маршруты с той же самой длиной пути. Если найден маршрут с более коротким путем, то матрица ot начинает формироваться заново. Рекурсия в commi2() и commi1() устроена совершенно одинаково.

![]()
Контрольный пример. Пусть рассматривается матрица расстояний U, приведенная перед функцией commi(). Найти все решения задачи коммивояжера для начального пункта 0 можно так:

Каждое из пяти решений занимает в полученной матрице одну строку, в которой первые восемь элементов - это маршрут, а последний элемент - его длина.
- Ананий В. Левитин Глава 3. Метод грубой силы: Задача коммивояжера // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Algorithms. — М.: «Вильямс», 2006. — С. 159-160. — ISBN 0-201-74395-7
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- В.И. Мудров Задача о коммивояжере. — М.: «Знание», 1969. — С. 62.