Level Sets for Image Segmentation
Erick Cantu-Paz, Samson Cheung, Abel Gezahegne, Cyrus Harrison, Chandrika Kamath, Nu Ai Tang
Sourse of information: https://computation.llnl.gov/casc/sapphire/levelsets/levelsets.html
Segmentation is an important technique used in image processing to
identify the objects in the image. As we work with data from simulations,
observations, and experiments, we are interested in segmentation techniques
that can be applied in a robust and efficient way to both image and mesh
data. Mesh data is frequently unstructured; this precludes the direct
application of techniques that were originally developed for the more
structured image data. One solution to this problem is the use of PDE-based
techniques such as level sets or implicit active contours (Osher and Sethian
1988, Osher and Paragios 2003, Sethian 2003).
The idea behind active contours, or deformable models, for image
segmentation is quite simple. The user specifies an initial guess for the
contour, which is then moved by image driven forces to the boundaries of the
desired objects. In such models, two types of forces are considered - the
internal forces, defined within the curve, are designed to keep the model
smooth during the deformation process, while the external forces, which are
computed from the underlying image data, are defined to move the model
toward an object boundary or other desired features within the image.
There are two forms of deformable models. In the parametric form, also
referred to as snakes, an explicit parametric representation of the curve is
used. This form is not only compact, but is robust to both image noise and
boundary gaps as it constrains the extracted boundaries to be smooth.
However, it can severely restrict the degree of topological adaptability of
the model, especially if the deformation involves splitting or merging of
parts. In contrast, the implicit deformable models, also called implicit
active contours or level sets, are designed to handle topological changes
naturally. However, unlike the parametric form, they are not robust to
boundary gaps and suffer from several other deficiencies as well (Suri and
others 2002).
Our main motivation for investigating level set techniques was to better
understand their pros and cons relative to the more traditional image
segmentation techniques. Some of our early work is summarized in (Weeratunga
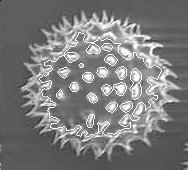
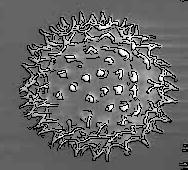
and Kamath 2004). Figure 1 shows the results obtained using level sets to
segment a grain of pollen from the background. To obtain the outer boundary
of the grain, we started with an initial level set at the boundary of the
image. To obtain the structures on the inside of the pollen grain, we
started with an initial level set that was a closed curve around a point on
the inside. This curve evolved to identify the boundaries of all the spines
inside the grain. The contours generated by the level sets are closed
contours. This is in contrast with edge detection methods such as the Canny
technique which typically requires a post-processing step to generate closed
contours. However, relative to the Canny method, the level sets are far more
computationally intensive, especially when used to segment a complex image
such as the inside of the pollen grain.

 a b c
a b c
Figure 1. Panels (a) and (b) illustrate the use of level sets in
segmenting a pollen grain. In (a), the initial curve was at the boundary of
the image, while in (b), the initial curve was a closed contour around a
point on the inside of the pollen grain. The boundary is identified in
white. Panel (c) is the output of the Canny edge detector, with the edges in
black. The pollen image is a Scanning Electron Microscope image of the
Anisodontea Bush Pollen and was obtained from the CCI Web Page.
Our current work focuses on understanding the sensitivity of the level set
method to various options such as the role of reinitialization, the
placement of the initial contour(s), the strength of the balloon force, the
role of the doublet term, etc.
Acknowledgments
This work was done in collaboration with Dr. Sisira Weeratunga of Lawrence Livermore National Laboratory.
References
S. Osher and J. A. Sethian, Fronts propagating with curvature dependent
speed: Algorithms based on Hamilton-Jacobi Formulations, Journal of
Computational Physics, volume 79, pp. 12-49, 1988.
S. Osher and N. Paragios, Geometric Level Set Methods in Imaging, Vision,
and Graphics, Springer-Verlag, New York, 2003.
J. Sethian, Level Set Methods and Fast Marching Methods: Evolving Interfaces
in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials
Science, Cambridge University Press, Cambridge, UK, 2003.
J. Suri, L. Liu, S. Singh, S. Laxminarayan, X. Zeng, L. Reden, Shape
recovery algorithms using levels sets in 2-D/3-D Medical Imagery: A
state-of-the-art review, IEEE Transactions on Information Technology in
Biomedicine, volume 6, No. 1, 2002.
Weeratunga S. and C. Kamath, "An investigation of implicit active contours
for scientific image segmentation," Video Communications and Image
Processing, SPIE Electronic Imaging, San Jose, January 2004,
UCRL-CONF-200711
J. Weickert and G. Kuhne, Fast methods for implicit active contour
models,Technical report, Preprint No. 61, Universitat des Saarlandes, 2002.