An Attribute-Based Image Segmentation Method

M.C. de Andrade^a, G. Bertrand^b A.A. de Araújo^c

^aCentro de Desenvolvimento da Tecnologia Nuclear - CDTN, 31270-010 Belo Horizonte - MG, Brazil
^bEcole Supérieure d'Ingénieurs en Electrotechnique et Electronique, ESIEE, Noisy-le-Grand, France
^cUniversidade Federal de Minas Gerais - UFMG/DCC, 30161-970 Belo Horizonte - MG, Brazil

Sourse of information: http://www.scielo.br/scielo.php?pid=S1...=sci_arttext

This work addresses a new image segmentation method founded on Digital Topology and Mathematical Morphology grounds. The ABA (attribute based absorptions) transform can be viewed as a region-growing method by flooding simulation working at the scale of the main structures of the image. In this method, the gray level image is treated as a relief flooded from all its local minima, which are progressively detected and merged as the flooding takes place. Each local minimum is exclusively associated to one catchment basin (CB). The CBs merging process is guided by their geometric parameters as depth, area and/or volume. This solution enables the direct segmentation of the original image without the need of a preprocessing step or the explicit marker extraction step, often required by other flooding simulation methods. Some examples of image segmentation, employing the ABA transform, are illustrated for uranium oxide samples. It is shown that the ABA transform presents very good segmentation results even in presence of noisy images. Moreover, it's use is often easier and faster when compared to similar image segmentation methods.

1. Introduction

This paper describes the ABA (Attribute Based Absorption) transform, a new image segmentation method founded on Digital Topology and Mathematical Morphology grounds. The ABA transform was originally conceived to simplify the segmentation of ceramic materials, whose images often present challenges, like illumination gradients, excessive number of minima, ill-defined regions (grains, pores, etc.), broken contours, etc.

A great number of image segmentation methods is available in the technical literature to deal with this kind of problem. Several efficient image segmentation methods are known as the watershed the dynamics, waterfall, h-domes extinction functions and attribute opening. A significant part of these methods, including the ABA transform, employ the powerful flooding simulation technique. The flooding simulation, however, is very sensitive to noise requiring an image smoothing step before the image segmentation. The ABA transform acts at the scale of the significant structures of the image thus avoiding the smoothing step. Derived from the watershed, the ABA transform incorporates a set of simple topological rules, which merges the non-significant regions of the image taking into account some of its geometric attributes, thus reducing the typical over-segmentation and producing a segmented image in one single step.

2. Materials and Methods

Routine procedures in quality control often require the determination of the volumetric grain size distribution to characterize a given material, since many of the its physical properties can be infered from this distribution. The characterization process usually depends on an image analysis step, which, by its turn, requires an image segmentation step. The segmentation can be done by hand or by an automatic or semi-automatic procedure and this choice usually depends on the problem and on the image quality. Tha ABA transform is classified as a semi-automatic image segmentation method.

To illustrate the ABA transform some typical ceramical samples of uranium oxide, prepared at the CDTN material's lab, are presented. These samples are sinterized pellets of uranium oxide that have been submitted to chemical, thermal and mechanical treatment. The images were photographed from an optical microscope and the resulting micrographs were digitized with a scanner.

Many microscopic images, like the ones here shown, reveal a microstructure composed of individual regions separated by thin gaps. As an example, Fig. 1a shows a highly magnified cross-section of a uranium oxide sample. This ceramic material is compound of several grains whose borders should be correctly extracted in order to evaluate the grain size distribution. Figure 1b, the negative image, shows the grains as darker regions, separated by gaps as brighter regions. The negative image is useful in the flooding simulation process.

Figure 1. Micrograph of a higly mignified cross section of a uranium oxide sample: (a) original, and (b) negative image.

Very few of the known image segmentation methods are robust enough to correctly extract the grain's borders. Usually the images present illumination gradient, noise, and defects that preclude the use of conventional segmentation techniques. Unless the segmentation is done by hand, automatic or semi-automatic segmentation require more effective methods.

Image segmentation based on the watershed transform is well suited for this task. However, despite its robustness the watershed transform can not be directly applied to an image, because it would produce a strongly over-segmented image as shown in Fig. 2b. The over-segmentation is often due to the excessive number of local minima present in the original non-filtered image, as shows Fig. 2a. Achieving a suitable segmentation means to suppress, someway, all the non-significant minima present in the image.

Figure 2. Micrograph of a higly mignified cross section of a uranium oxide sample: (a) minima shown as white spots, and (b) over-segmentation resulting from the watershed transform applied to the non-filtered image (a).

2.1. The watershed transform

The flooding simulation technique interprets a gray level image as a topographic relief. To each gray level is assigned a height proportional to its value. The result is a “3D” image presenting several valleys separated by mountains, as illustrates Fig. 3. Seen from above, the landscape would have basins corresponding to the regions of interest separated by dams called watersheds. The water, supposed to come from `holes' carved at the bottom of each basin, propagates, step by step, inside each catchment basin (CB).

Figure 3. 3D representation of the gray level image of Fig. 1.

The watershed transform is based on a stepwise flooding simulation. It is a recursive and inherently serial process since the current flooding level is always dependent on the immediately precedent one. A formal definition of the concept of watershed transform of a digital image can be found in the paper presented by Vincent. The watershed segmentation is a two step procedure: an intelligent step consisting in the extraction of significant minima, often requiring the human judgment, and a mechanical step where the watershed algorithm, guided by the extracted minima or by markers associated to those minima, is applied to the image. As a rule, to correctly segment an image, its particularities and the expected segmentation results must always be taken into account.

2.2 The ABA transform

The ABA transform is an image segmentation method derived from the watershed transformation. It can be classified as a region-growing method by a flooding simulation. The ABA algorithm treats the image as a relief flooded from all its local minima, which are progressively detected and conditionally merged as the water fills up the relief. The merging process is guided by the basin's geometric attributes and a set of simple rules allowing the quick and reliable segmentation of a wide class of images without the need to preprocessing the images. The fine tuning of parameters often leads to well-segmented images presenting very low over or under-segmentation rates.

Figure 4 shows an arbitrary 1D vertical profile extracted from the uranium oxide micrograph presented in Fig. 1. It can also be seen as a transversal slice of Fig. 3. The prominent peaks represent the grain boundaries while the small ones are often due to noise or to irregularities in the material's surface.

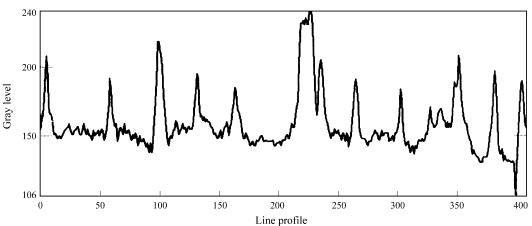
Figure 4. Arbitrary line profile of the uranium oxide micrograph showed in Fig. 1. The spaces between two relatively high peaks represent catchment basis, i.e. grains. The small peaks inside the catchment basins are due to noise introduced during the image acqisition step.

The areas inside two relatively high peaks represent the catchment basins (CBs), i.e., in this image the grains, whose boundaries should be detected. A closer inspection of this profile shows that the non-significant minima, which are responsible for the over-segmentation, are located between two small peaks. To achieve a reliable segmentation all these small, non-significant, minima should be somehow ignored. The relative difference between peak heights then suggests an effective way to segment this image. It is possible to merge all the small basins taking into account not only their depths but, as well as, their areas and volumes.

Since the relief is being flooded from the bottom of each catchment basin, all local minima are progressively detected and eventually merged as the flooding takes place, as illustrated in Fig. 5. The ABA algorithm embeds a set of rules into the original non-hierarchical watershed algorithm to guide the catchment basins merging process. Combining these rules it is possible to merge, to delay or even to prevent the catchment basin's merging. The method was implemented to allow the free combination of these parameters, i.e.; the user has the option to chose which parameters to use. This simple expedient allows the direct segmentation of the original image without the need of previous filtering or markers detection steps, usually required by the watershed transform. The catchment basin's depths, areas and volumes are constantly monitored for each basin as the flooding occurs. An additional set of rules, providing intrinsecal filtering capacity, is used to suppress the noise. Figure 6 shows snapshots of the flooding process for different values of the height attribute.

Figure 5. Attributes of a catchment basin.

Figure 6. Time sequence absorptions for different h values (depth) during flooding with ABA.

3. Results and Discussion

Figures 7a , 7c and 7e show uranium oxide samples presenting grains, pores and acquisition defects. The presence of strong noise and irregular lighting, prevent the direct segmentation of these images by conventional techniques. Applying an histogram thresholding technique, for example, would produce thick, broken, deviated boundaries and the regions would show undesirable holes due to the interior pores. Figures 7b, 7d and 7e present the respective ABA segmentation results. In these examples, the ABA transform was directly applied to the negative of original images. It can be seen that, despite the initial noise, almost all contours were correctly detected and the grains are clean and well defined. The ABA transform has been applied to several samples of ceramic images producing very good results. The determination of the 3D-grain size distribution can be done from these segmented images employing a stereometric method like the Saltykov method.

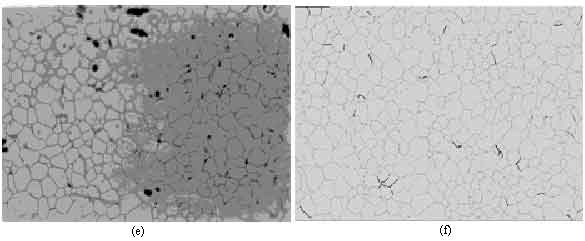
Figure 7 (cont). ABA transfom segmentation for three uranium oxide samples: (a), (c) and (e) are original noisy images, (b), (d) and (f) are ABA tranform segmented images.

4. Conclusions

When applied to real ceramic micrographs, the ABA method has proved to be efficient even in the presence of strong noise. The ABA transform is a practical solution to the over-segmentation problem. It employs a simple set of “merging criteria” thus enabling faster image segmentation and avoiding the explicit markers detection step found in conventional methods. Despite the need of interactively selecting the thresholds for the image geometrical attributes, the ABA segmentation overall execution time are very good. The ABA transform preserves the linear execution time of the watershed algorithm. It can be applied to a wide class of images, specially to those presenting similar segmentation problems like the ones here shown. The ABA transform is not restricted to the 2D image domain, 3D or multi-dimensional images could be also be considered.

Acknowledgments

The authors would like to acknowledge ESIEE- France, CNPq, CAPES/MEC, FAPEMIG and CDTN /CNEN for the financial and technical support.

References

1. Andrade, M.C. “Um Mйtodo Topolуgico de Segmentaзгo de Imagens por Atributos”. Ph.D. Thesis. Universidade Federal de Minas Gerais, DCC-UFMG, 1998.

2. Andrade, M.C. et al., “Segmentation of microscopic images by flooding simulation: a catchment basins merging algorithm”. In: Proceedings of Society for Imaging and PhotoOptical Engineering- SPIE, San Jose, USA, 1997.

3. Kong, T.; Rosenfeld, A. Digital Topology: Introduction and Survey, Computer Graphics and Image Processing - CGIP, v. 48, p. 357-393, 1989.

4. Bertrand, G. et al. A topological approach to image segmentation. In: Proceedings of Society for Imaging and PhotoOptical Engineering- SPIE, Vision and geometry V, v. 2826, p. 65-67, 1996.

5. Serra, J. Image Analysis and Mathematical Morphology, Academic Press, 1982.

6. Vincent, L.; Soille, P. “Watersheds in digital spaces: An efficient algorithm based on immersion simulations”. Transactions on Pattern Analysis and Machine Intelligence, v. 13, n. 6, p. 583-598, 1991.

7. Meyer, F. “Un algorithme optimal de ligne de partage des eaux”. Congress AFCET, RFIA, Lyon, 1991.

8. Grimaud, M. “La geodesie numerique en morphologie mathematique. Application a la detection automatique de microcalcifications en mammographie numerique”, Centre de Morphologie Mathematique, Йcole Nationale Supйrieure de Mines de Paris - ENSMP, Ph.D. Thesis, 1991.

9. Beucher, S. “Segmentation d'image et Morphologie Mathematique” , Centre de Morphologie Mathematique, ENSMP, Ph.D. Thesis, 1990.

10. Vachier, C. “Extraction de characteristiques, segmentation d'image et morphology mathematique”, Ph.D. Thesis, Centre de Morphologie Mathematique, ENSMP, 1995.

11. Breen, E.J.; Jones, R. Attribute openings, thinnings and granulometrics. Computer Vision ans Image Processing, v. 64, n. 3, p. 377-389, Nov. 1996.

12. Saltykov, “Stereometrische Metallographie”, VEB, 1974.