Исследование нелинейных инверсных преобразований в системе MATLAB
Савченко Д.А., Самощенко А.В.
Источник: Тезисы доклада на V международной студенческой
научно-технической конференции "Информатика и компьютерные технологии 2009",
24-26 ноября 2009 г., ДонНТУ, Донецк.
Конформные преобразования применяются для обработки изображений с
целью достижения некоторых эффектов. Особенностью нелинейных
конформных преобразований является наличие свойства сохранения
формы объекта применительно не ко всей фигуре, а только к малым
её частям. Вследствие этого углы между гладкими кривыми сохраняются.
В работе изображение деформируется с использованием преобразований типа (z+1/z)/2.
Функции для открытия и отображения изображения в системе MATLAB:
A=imread('figures4.png');
figure, imshow(A);

Рисунок 1. 1 – Исходное изображение
Для применения преобразований используются функции maketform и imtransform.
Функция maketform формирует TFORM структуру. В качестве первого параметра (TRANSFORMTYPE – тип преобразовании) необходимо указывать 'custom'. Данный параметр означает, что формирование структуры основывается на функции, предоставленной пользователем, например, типа (z+1/z)/2.
Следующие два параметра указывают количество измерений входящего и выходящего изображений - 2. Далее необходимо передать указатели на две функции – прямую и инверсную. В качестве прямой функции не передаётся ничего, используя пустые квадратные скобки - []. В поле адреса инверсной функции указывается @ipex004. Последний параметр - массив, в котором будут сохранены параметры преобразования.
В приведенном ниже примере последний параметр передаваться не будет:
conformal=maketform('custom', 2, 2, [], @ipex004, []);
В результате сформируется структура, которая будет содержать параметры, переданные функции.
Функция инверсных преобразований:
function U=ipex004( X, t )
Z=complex(X(:, 1), X(:, 2));
W=(Z+1./Z)/2;
U(:, 2)=imag(W);
U(:, 1)=real(W);
Параметр X – массив координатных векторов приведенных к выходному пространству. Каждый вектор содержит по 2 значения (зависит от количества измерений). Количество векторов равняется количеству пикселей изображения в выходном пространстве.
Для применения преобразования векторы представляются в виде комплексных чисел и записываются в массив Z. Следующий шаг – это выполнение инверсных преобразований W=(Z+1./Z)/2. После операции из комплексных чисел формируются векторы.
Функция imtransform преобразует изображение.. Первый параметр – изображение, которое необходимо преобразовать. Второй параметр – структура типа TFORM. Третий параметр – тип интерполяции: 'nearest', 'bilinear', 'bicubic'. Следующие 4 параметра uData, vData, xData, yData, которые представляют собой вектор-строку из двух параметров. uData, vData описывают относительное пространственное положение входного изображения, xData, yData – выходного.
uData=[ -1.25 1.25];
vData=[ 0.75 -0.75];
xData=[ -2.4 2.4 ];
yData=[ 2.0 -2.0 ];
Параметр ‘Size’ описывает размеры выходного изображения в пикселях – длину и ширину. Желательно, чтобы размеры выходного изображения были пропорциональны значениям xData, yData – относительным пространственным положениям выходного изображения. Последний параметр – 'FillValues’ определяет цвет, которым будут заполнятся «пустые» части изображения. В примере используется значение 255 – белый цвет.
B=imtransform( A, conformal, 'cubic', 'UData', uData,'VData', vData, 'XData', xData,'YData', yData,'Size', [300 360], 'FillValues', 255);
figure, imshow(B);
title('Transformed Image');
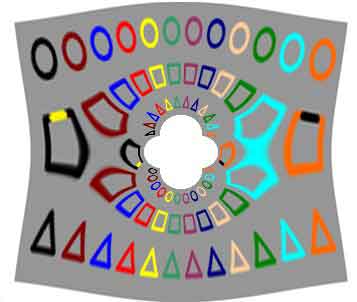
Рисунок 1. 2 – Преобразованное изображение
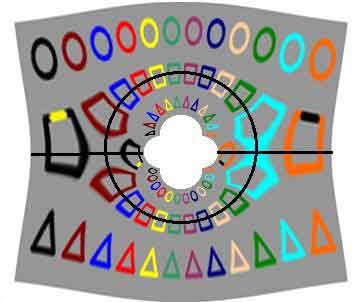
Рисунок 1. 3 – Преобразованное изображение с контурами
В результате получилось изображение, в котором объекты исходного повторяются дважды (рис1.2). Чтобы лучше понять произошедшие преобразования, необходимо навести контурные линии (рис 1.3).
Внешние два фрагмента представляют собой исходное изображение, которое подверглось небольшим нелинейным искажениям. Чем ближе к центру, тем сильнее деформация.
Внутренние два фрагмента изображения тоже представляют собой исходное изображение. Но есть два существенных отличия. Над горизонтальной осью результирующего изображения находятся объекты нижней части исходного изображения. Соответственно под осью находятся объекты верхней части начального рисунка. Фрагменты внутри контурного круга подверглись большей деформации.
В итоге верхний фрагмент вне окружности и нижний внутри окружности – образовались от одной и той же части исходного изображения. Но разные части изображений изгибались в разные стороны, и внутренний фрагмент подвергся более сильной деформации. Аналогичным преобразованиям подверглись оставшиеся два фрагмента.
Можно немного изменить функцию преобразований.
function U = ipex006( X, t )
Z = complex(X(:,1),X(:,2));
W = (Z + 1./Z)/2;
q = 0.5 <= abs(Z) & abs(Z) <= 2;
W(~q) = complex(NaN,NaN);
U(:,2) = imag(W);
U(:,1) = real(W);
В данной функции используется аналогичная формула W = (Z + 1./Z)/2. Но следующие две строчки кода «скругляют» внутреннюю и внешнюю части результирующего изображения:
q = 0.5 <= abs(Z) & abs(Z) <= 2;
Формируется логический вектор q, который состоит из 0 и 1. Если в полученном векторе i-тый элемент равен 0, то длина соответствующего координатного вектора не в пределах [0.5 2]. Иначе элемент вектора q содержит логическую единицу, что означает принадлежность длины вектора диапазону.
W(~q) = complex(NaN,NaN);
Для всех элементов уже преобразованного массива комплексных чисел, которым соответствует логический нуль массива q, присваивается значение NaN – Not A Number (не число). Поэтому крайние фрагменты изображения сформированы не будут.
function void = conform2(void)
A=imread('figures4.png');
conformal=maketform('custom', 2, 2, [], @ipex006, []);
uData=[ -1.25 1.25]; % Граница для REAL(w)
vData=[ 0.75 -0.75]; % Граница для IMAG(w)
xData=[ -2 2 ]; % Граница для REAL(z)
yData=[ 2 -2 ]; % Граница для IMAG(z)
B=imtransform( A, conformal, 'cubic', 'UData', uData,'VData', vData, 'XData', xData,'YData', yData,'Size', [360 360], 'FillValues', 255);
figure, imshow(B);
title('Transformed Image');
end
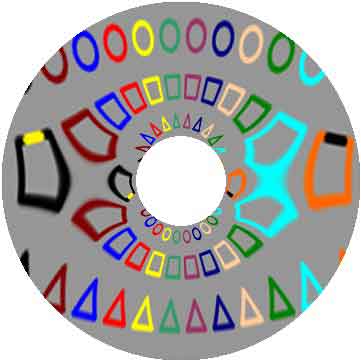
Рисунок 1.4 – «Скруглённое» изображение
Литература:
-
Гонсалес Р. Цифровая обработка изображений в среде MATLAB / Гонсалес Р., Вудс Р., Эддинс С. ; пер. с англ. В.В. Чепыжова. – Москва: Техносфера, 2006. – Глава 5. – С. 195 – 205. – ISBN 5-94836-092-X.
-
Exploring a Conformal Mapping [Электронный ресурс] – Режим доступа к статье: http://www.mathworks.com/products/demos/image/conformal_mapping/tform4.html.