Аннотация

Секирин А.И., Шептуля А.В. Система поддержки принятия решения формирования и регулирования ценовой политики предприятия. В статье рассматривается вопрос формирования и регулирования ценовой политики предприятия с целью максимизации прибыли путем установления максимально возможных цен при максимальных продажах.

Актуальность проблемы. Для предприятия вопрос формирования и регулирования ценовой политики играет огромную роль. От того, как проводится ценообразование на предприятии, зависит его прибыль. Кроме того, в существующих сейчас условиях рыночной экономики цена стала существенным фактором в конкурентной борьбе.

Обзор существующих методов. Сегодня учеными разработано множество различных методов прогнозирования, которые по-разному комбинируются в рамках того или иного подхода. Так к методам прогнозирования объемов продаж относятся: методы экспертных оценок и казуальные методы. Точечный прогноз объема продаж, который относится к методам экспертных оценок, содержит наименьший объем информации, поэтому может быть ошибочным. Сложностью применения казуальных методов является то, что применение многофакторного прогнозирования требует решения сложной проблемы выбора факторов, которая не может быть решена чисто статистическим путем, а связана с необходимостью глубокого изучения экономического содержания рассматриваемого явления или процесса. Для решения поставленной задачи предлагается выбрать метод анализа и прогнозирования динамических рядов.

Математическая постановка задачи. Перед нами стоит задача максимизации прибыли предприятия. Для построения ее формальной схемы (модели) введем общие обозначения.

Буквой N обозначим множество всех лиц, принимающих решение (ЛПР). Пусть N=1. Предположим, что множество всех стратегий ценообразования ЛПР предварительно изучено и описано математически. Обозначим их через X₁ , X₂ ,..., X_n. После этого процесс принятия решения всеми ЛПР сводится к следующему формальному акту: ЛПР выбирает конкретный элемент из своего допустимого множества решений 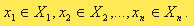В результате получается набор х =(x₁ ,..., x_n) выбранных решений, который мы называем ситуацией.

Для оценки ситуации х с точки зрения выбора наилучшей стратегии ценообразования для максимизации прибыли строятся функции f₁ ,..., f_n, ставящие в соответствие каждой ситуации х числовые оценки f₁(x) ,..., f_n(x) – доходы фирмы в ситуации х. Тогда цель ЛПР формализуется следующим образом: выбрать такое свое решение , чтобы в ситуации х =(х₁ ,...,х_n) число f_i(х) было как можно большим. Пусть нам удалось математически описать все те условия, при которых происходит принятие решения (описание связей между управляемыми и неуправляемыми переменными, описание влияния случайных факторов, учет динамических характеристик и т. д.). Совокупность всех этих условий для простоты обозначим одним символом .

Таким образом, общая схема задачи принятия решения может выглядеть так:

N; X₁,...,X_n; f₁(x),...,f_n(x);

Конкретизируя элементы модели, уточняя их характеристики и свойства, можно получить тот или иной конкретный класс моделей принятия решения. С помощью данной схемы можно написать экстремальную задачу двух вида:

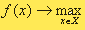- максимизация прибыли.

В экстремальной задаче явно учитывается фактор времени, поэтому она называется задачей оптимального управления.

В случае задачи максимизации прибыли элементы модели (1) зависят явно от времени, т. е. процесс принятие решения представляет собой многоэтапный дискретный или непрерывный во времени процесс, поэтому задача называется динамической. Также элементы модели (1) не содержат случайных величин и вероятностных явлений, поэтому задача называется детерминированной.

Оптимизация. Составим описание «Задачи формирования и регулирования ценовой политики предприятия».

Предположим, что предприятие может потратить наличный капитал K в следующем квартале на закупку товара N видов, требуется определить соответствующие доли затрат.

Пусть x_j, j= 1,N – величина капитала, потраченного на товар j-го вида. Тогда на переменные накладываются следующие ограничения:

Предположим, что фирма имеет статистические данные о доходности от продаж r_j(t), j= 1,N, t= 1,T, для каждого вида товара за Т периодов, начиная с t₀. Доходность r_j(t) определяется как доход за период t на одну денежную единицу затрат на товар j. Величину r_j(t) можно определить из соотношения

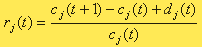
с _j(t) - цена товара j-го типа на начало периода t;

d _j(t) - суммарная прибыль, полученная за период t.

Значения r_j(t) непостоянны и могут сильно колебаться от периода к периоду. Эти значения могут иметь любой знак или быть нулевыми. Для оценки целесообразности затрат на покупку товара j-го вида следует вычислить среднюю или ожидаемую доходность M_j от товара вида j.

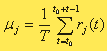
Средний или ожидаемый доход E(x) от товаров определяется следующим образом:

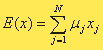
Наряду со средним (ожидаемым) доходом важнейшей характеристикой является риск, связанный с затратами на товар. В качестве меры инвестиционного риска можно рассматривать величину отклонения доходности от ее среднего значения за последние T периодов. Тогда оценкой инвестиционного риска для товара вида j является дисперсия, которая вычисляется по формуле

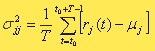
Кроме того, курсы некоторых ценных бумаг подвержены совместным колебаниям (примерами таких ценных бумаг являются акции нефтяных и автомобильных компаний). Оценкой инвестиционного риска для пары видов ценных бумаг, принадлежащих к взаимосвязанным областям экономики, является ковариация, которая вычисляется по формуле

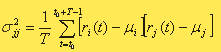
Заметим, что при i=j эта величина сводится к дисперсии бумаг вида j.

Таким образом, в качестве меры инвестиционного риска закупки товаров может служить величина:

На основании описанных характеристик - ожидаемый доход E(x) и инвестиционный риск V(x) - рассмотрим несколько моделей, оптимизирующих задачу.

Модель 1. Максимизация ожидаемого дохода при ограничении на общий объем затрат на товары.

Модель имеет вид:

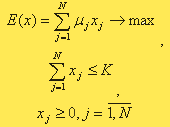
Данная модель является моделью линейного программирования (ЛП). Оптимальное решение x*={x*_j}, j= 1,N, E*=(E*_j) может быть найдено симплекс-методом.

Закупаемые товары могут формироваться с учетом различных ограничений, связанных с политикой фирмы.

Модель 2. Минимизация закупочного риска при заданном среднем доходе.

Владельцы закупленного товара могут быть заинтересованы в получении заданного ожидаемого дохода R при минимальном риске. Оптимизационная модель в этом случае имеет вид:

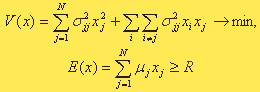
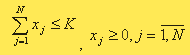
Данная модель является моделью квадратичного программирования, так как целевая функция квадратичная, а ограничения линейные. Оптимальное решение x*={x*_j}, j= 1,N, E*=(E*_j) может быть найдено методом квадратичного программирования.

Топология нейросети и временные ряды. В качестве основной задачи выбрана максимизация прибыли предприятия путем установления максимально возможных цен при максимальных продажах.

Для реализации задачи будем использовать следующую схему:

Рисунок 1 – Схема технологического цикла предсказаний рыночных временных рядов

Рассмотрим метод погружения. Для динамических систем доказана следующая теорема Такенса: если временной ряд порождается динамической системой, т.е. значения X_t есть произвольная функция состояния такой системы, существует такая глубина погружения d (примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда. Таким образом, выбрав достаточно большое d , можно гарантировать однозначную зависимость будущего значения ряда от его d предыдущих значений: X_t = f(X_t - d), т.е. предсказание временного ряда сводится к задаче интерполяции функции многих переменных. Нейросеть далее можно использовать для восстановления этой неизвестной функции по набору примеров, заданных историей данного временного ряда.

Формирование входного пространства признаков. На рисунке 1 видно, что увеличение ширины окна погружения ряда приводит, в конце концов, к понижению предсказуемости - когда повышение размерности входов уже не компенсируется увеличением их информативности.

Рассмотрим структуру свободной розничной цены.

Таблица 1. Структура свободной розничной цены.

Свободная розничная цена
Свободная отпускная цена	Торговая надбавка	НДС торговли

Свободная розничная цена товара, реализуемого с учетом посредника (оптового торгового предприятия или снабженческо-сбытовой организации), включает свободную отпускную цену без НДС, надбавки посредника (оптовые надбавки) и НДС посредника( цену закупки), а также торговую надбавки.

Входное пространство признаков сформируем следующим образом:

• 1. Средняя норма прибыли
• 2. Спрос на продукцию
• 3. Издержки
• 4. Цены конкурентов
• 5. Средний достаток потребителя
• 6. Курс доллара
• 7. Сезонность
• 8. Цикличность
• 9. Свободная отпускная цена

Для обучения нейросети недостаточно сформировать обучающие наборы входов-выходов. Необходимо также определить ошибку предсказаний сети. Среднеквадратичная ошибка, используемая по умолчанию в большинстве нейросетевых приложений, не имеет большого "финансового смысла" для рыночных рядов.

При обучении нейросети данные разбиваются на три выборки: обучающая, валидационная и тестовая. Первая используется для обучения, вторая - для выбора оптимальной архитектуры сети и /или для выбора момента остановки обучения. Наконец, третья, которая вообще не использовалась в обучении, служит для контроля качества прогноза обученной нейросети. В качестве обучающей выборки используются значения входных признаков. Программная реализация задачи выполнена на языке программирования C#.

Выводы.

В качестве основной задачи формирования и регулирования политики предприятия была принята максимизация прибыли путем установления максимально возможной цен при максимальных продажах. В результате работы был проведен анализ литературы по системам поддержки принятия решения, методам прогнозирования, оптимизации. Был сформулирована математическая постановка задачи, ее оптимизация, выбрана схема реализация задачи, топология нейросети, программная реализация выполнена на языке программирования C#.

Литература:

1. Гайдрик К.В. Системы поддержки принятия решений: эволюция концепции и некоторые перспективы. / К.В. Гайдрик - Кишинев, Молдова. Институт математики АН РМ, 1988. - 6 с.

2. Система поддержки принятия решений [Электронный ресурс] – Режим доступа к статье: http://ru.wikipedia.org/wiki/Система_поддержки_принятия_решений.html

3. Предсказание финансовых временных рядов. AB Forex. [Электронный ресурс] – Режим доступа к статье: http://www.abforex.ru/download/vremya_ab%20forex.rar

4. Новиков Д.А. Активный прогноз. / Д.А. Новиков, А.Г. Чхартишвили – М.: ИПУ РАН, 2002. – 101 с.

5. Сергей Шумский. Предсказание финансовых временных рядов [Электронный ресурс] – Режим доступа к статье: http://articles.mql4.com/542

6. Прогнозирование цен с помощью нейросетей [Электронный ресурс] – Режим доступа к статье: http://articles.mql4.com/461

7. Есипова В.Е. Цены и ценообразование. / В.Е. Есипова. – СПб: Питер, 2001. - 464 с.

8. Харчистов Б.Ф. Методы оптимизации: Учебное пособие. / Б.Ф. Харчистов – г. Таганрог: Изд-во ТРТУ, 2004. – 140 с.

9. Новиков Д.А. Механизмы функционирования многоуровневых организационных систем. / Д.А. Новиков – М.: Фонд "Проблемы управления", 1999. – 161 с.

10. Салимжанов И.К. Ценообразование: учебник. / И.К. Салимжанов. – М. : КНОРУС, 2007. – 304 с.

11. Бурков В.Н. Экономико-математические модели управления развитием отраслевого производства. / В.Н. Бурков, Г.С. Джавахадзе - М.: ИПУ РАН, 1997. – 64 с.

12. Лушин С.И. Ценность. Цена. Стоимость. / С.И. Лушин - М.: Юрист, 2001. - 80 с.

13. Корнеев С.В. Системы поддержки принятия решений в бизнесе. Журнал "Сети & Бизнес" (№6, 2005) [Электронный ресурс] – Режим доступа к статье: http://www.sib.com.ua/arhiv_2005/...