Автор: Александр Коренев
Источник: http://www.cfin.ru/finanalysis/math/statistical_method.shtml
Введение
В этой статье мы на примере рассмотрим один из статистических методов прогнозирования продаж. Мы будем прогнозировать прибыль, а точнее размер месячной прибыли. Совершенно аналогично можно делать прогнозы и других показателей продаж: выручка, объем продаж в натуральных единицах, количество сделок, количество новых клиентов и т.д.
Описанный в статье метод прост (относительно, конечно) и не привязан к специализированным программам. В принципе, для составления прогноза достаточно было бы бумаги, карандаша, калькулятора и линейки. Однако, это очень трудоемкий способ, поскольку в процессе возникает много рутинных вычислений. Поэтому мы будем использовать Microsoft Excel (версии 2000).
Помимо простоты у метода есть еще один важный плюс: для прогноза требуется небольшая статистика. Сделать прогноз на 2-3 месяца вперед можно, если есть статистика хотя бы за 13-14 месяцев. Ну а большая статистика дает возможность и прогноз делать на больший период.
Сбор и подготовка статистики продаж
Прогнозирование начинается, конечно, со сбора статистики продаж. Здесь нужно обращать внимание на то, чтобы все сделки были более-менее одного «масштаба», и чтобы количество сделок в месяц было достаточно большое.
Например, розничный магазин. Даже в небольшом магазине в месяц могут делаться тысячи и даже десятки тысяч покупок. Сумма каждой покупки, по сравнению с месячной выручкой, весьма мала — 0,0..01% от выручки. Это хорошая ситуация для прогнозирования.
Если прогноз делается для компании, работающей на корпоративном рынке, то нужно следить, чтобы количество сделок в месяц было хотя бы не менее 100, иначе для прогнозирования нужно применять другие методы. Также, если в статистике продаж встречаются крупные сделки, с суммой, например, около 10% от месячной выручки, то такие сделки надо исключать из статистики и рассматривать отдельно (опять же другими методами). Если крупные сделки не исключить, то они создадут в динамике «выбросы», которые могут сильно ухудшить точность прогноза.
Далее мы будем рассматривать пример со статистикой из таблицы 1. На рисунке 1 данные таблицы представлены в виде графика.
По этим данным мы будем составлять прогноз на 12 месяцев вперед.
| Период | № Периода | Прибыль | Период | № Периода | Прибыль |
| 2004-7 | 1 | 839 | 2005-5 | 11 | 3069 |
| 2004-8 | 2 | 1714 | 2005-6 | 12 | 2220 |
| 2004-9 | 3 | 2318 | 2005-7 | 13 | 1653 |
| 2004-10 | 4 | 2629 | 2005-8 | 14 | 3115 |
| 2004-11 | 5 | 2823 | 2005-9 | 15 | 3961 |
| 2004-12 | 6 | 3320 | 2005-10 | 16 | 4514 |
| 2005-1 | 7 | 3316 | 2005-11 | 17 | 4644 |
| 2005-2 | 8 | 3479 | 2005-12 | 18 | 5066 |
| 2005-3 | 9 | 3388 | 2006-1 | 19 | 4934 |
| 2005-4 | 10 | 3263 | - | - | - |

Рисунок 1 - График помесячной прибыли, данные из таблицы
Существуют две основные модели временного ряда: аддитивная и мультипликативная. Формула аддитивной модели: Yt = Tt + St + et Формула мультипликативной модели: Yt = Tt x St + et Обозначения: t - время (месяц или другой период детализации); Y - значение величины; Т — тренд; S — сезонные изменения; е - шум. Разница между моделями хорошо видна на рисунке 2, где приведены два ряда, с одинаковыми трендами, один ряд — по мультипликативной модели, другой — по аддитивной.
Примечание. Могут встречаться такие показатели продаж, у которых сезонные колебания практически отсутствуют.

Рисунок 2 - Примеры рядов: слева — по аддитивной модели; справа — по мультипликативной.
В нашем примере мы будем использовать мультипликативную модель.
Для каких-либо других данных, возможно лучше подошла бы аддитивная модель. Узнать на практике, какая модель подходит лучше, можно либо интуитивно, либо методом проб и ошибок.
Выделение тренда
В формулах моделей рядов динамики (Yt = Tt + St + et и Yt = TtSt + et) фигурирует тренд Tt, такой тренд мы будем называть «точным».
В практических задачах выделить точный (вернее, «почти точный») тренд Tt может оказаться технически очень сложно (см. например, пункт [5] в списке литературы).
Поэтому мы будем рассматривать приближенные тренды. Самый простой способ получения приближенного тренда — сглаживание ряда методом скользящего среднего с периодом сглаживания равным максимальному периоду сезонных колебаний. Сглаживание почти полностью устранит сезонные колебания и шум.
В рядах с детализацией по месяцам сглаживание нужно делать по 12-ти точкам (то есть по 12-ти месяцам). Формула скользящего среднего с периодом сглаживания 12 месяцев:

Где Mt — значение скользящего среднего в точке t; Yt — значение величины временного ряда в точке t.
Примечание. Очень редко, но все-же бывают динамики продаж, где длина полного период не только не равна году, но и «плавает». В таких случаях колебания, видимо, вызваны не сезонными изменениями, а какими-то другими, более мощными факторами.
Обратите внимание: поскольку мы вычисляем некоторый средний тренд за последние 12 месяцев, то в поведении приближенного тренда по сравнению с точным, происходит как бы запаздывание на 6 месяцев. Не смотря на то, что тренд, полученный методом скользящего среднего — это не точный, а приближенный (да еще и с запаздыванием), он вполне подходит для нашей задачи.
Прологарифмируем уравнение мультипликативной модели, и если шум et не очень большой, то получим аддитивную модель.

Здесь также обозначает шум. Тренд мы выделим (скользящим средним за 12 месяцев) именно для такой преобразованной модели. На рисунке 3 — графики и показателя и тренда Mt.
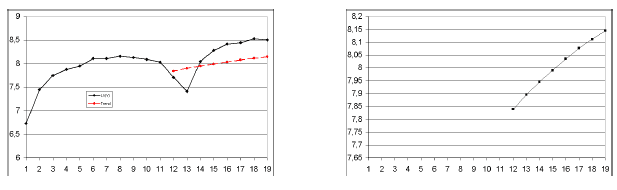
Рисунок 3 - График прологарифмированной величины показателя и тренда Ми скользящего среднего по 12-ти месяцам. Слева на одном графике и величина и тренд. Справа — тренд в увеличенном масштабе. По оси X — номера периодов.
Примечание. Если темпы динамики небольшие, скажем, 10-15% в год, то и с мультипликативной моделью можно работать как с аддитивной (не логарифмирую).
Прогноз тренда
Тренд мы получили, теперь нужно его спрогнозировать. Прогноз можно бы было получить, например, методом экспоненциального сглаживания (см. [4), но поскольку мы хотим прогнозировать максимально простым методом, то остановимся на обычной параметрической аппроксимации. В качестве функций приближения используем следующий набор:
Линейная функция: y = a + b × t.
Логарифмическая функция: y = a + b × ln(t)
Полином второй степени: y = a + b × t + c × t2
Степенная функция: y = a × tb
Экспоненциальная функция: y = a × eb × t
Хорошо бы было дополнить набор и другими функциями, но для этого возможностей Excel недостаточно, нужно использовать специализированные программы: Maple, Matlab, MathCad и т.д.
Качество приближения мы будем оценивать по величине достоверности аппроксимации R2. Чем ближе эта величина к 1 — тем лучше функция приближает тренд. Это верно не всегда, но в Excel нет других критериев оценки качества аппроксимации. Впрочем, критерия R2 нам будет достаточно.
На рисунках 4, 5, 6, 7 и 8и мы сделали аппроксимацию нашего тренда различными функциями и каждая функция аппроксимации продолжена на 12 точек вперед. И еще одна аппроксимация — на рисунке 9, полиномом 5-той степени.
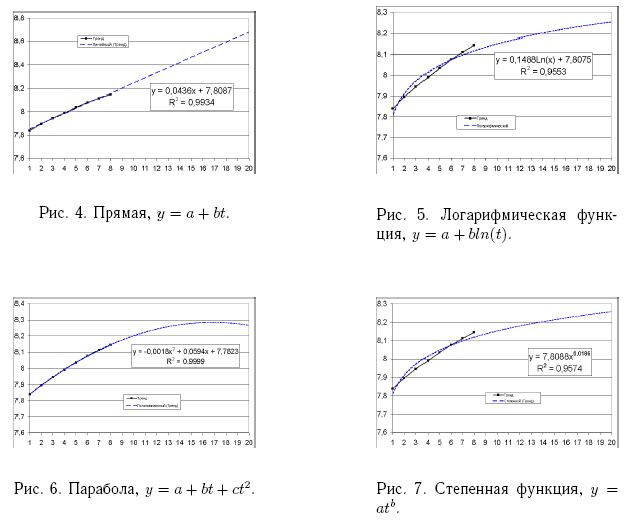
Обратите внимание: если некоторая функция хорошо приближает тренд, то это не всегда означает, что данная функция хорошо тренд прогнозирует. В нашем примере полином 5-той степени делает самое лучшее приближение по сравнению с другими функциями (R2 = 1) и, одновременно, дает самый нереальный прогноз.

По рисункам мы видим, что значение R2 ближе всего к единице у параболы (полином 5-той степени уже не рассматриваем). Следующая по качеству аппроксимация — прямая линия. Хотя формально парабола аппроксимирует лучше всех, но ее поведение, особенно перевал в отдаленных точках, представляется не очень правдоподобным. Тогда можно взять аппроксимацию прямой, но мы найдем компромисс: среднее арифметическое между параболой и прямой.
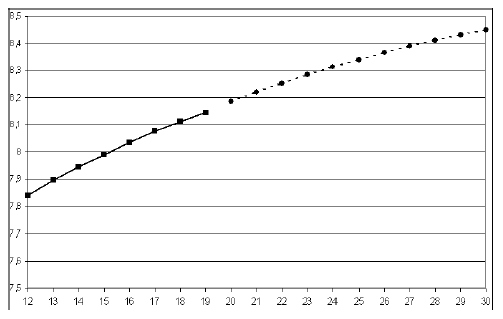
Рисунок 10 - Тренд Mt и его прогноз. По оси X — номер периода.
Результат прогноза тренда Mt — на рисунке 10. Итак, мы получили прогноз тренда.
Прогноз показателя
Прогноз тренда у нас есть. Теперь можно сделать прогноз самого показателя. Формула очевидна:
Ln(Yt+1) = 12 × Mt+1 – Ln(Yt) – Ln(Yt-1) – ... – Ln(Yt-10)
Yt+1 = exp(Ln(Yt+1))
До периода t = 19 у нас есть фактические данные. Для t = 20..31 у нас есть спрогнозированный тренд Mt, а значения показателя мы будем считать последовательно, сначала для t = 20, потом для t = 21 и т.д.
Результаты прогноза — на рисунке 11 и в таблице 2.
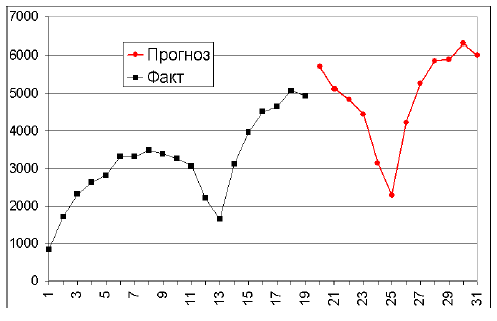
Рисунок 11 - Прогноз показателя. По оси X — номер периода.
Сравнение прогноза и реальных данных
На рисунке 12 — графики прогноза и фактических данных.
В таблице 3 приведено сравнение реальных данных и спрогнозированных. Посчитаны ошибки прогноза, абсолютные: Прогноз-Факт; и относительные: 100%*(Прогноз-Факт)/Факт.
Обратите внимание, что ошибки прогноза смещены в положительную сторону. Причина этого может быть как в несовершенстве метода, так и в каких-то объективных обстоятельствах, например, в изменении ситуации на рынке в прогнозируемом периоде.
Точность прогноза
Какую точность прогноза можно считать хорошей? Это во многом зависит от исходных данных и применяемой для прогноза модели.
| Период | № Периода | М | Ln(Y) | Y |
| 2006-2 | 20 | 8,1861 | 8,6494 | 5707 |
| 2006-3 | 21 | 8,2205 | 8,5408 | 5119 |
| 2006-4 | 22 | 8,2531 | 8,4816 | 4825 |
| 2006-5 | 23 | 8,2839 | 8,3987 | 4441 |
| 2006-6 | 24 | 8,3129 | 8,0533 | 3144 |
| 2006-7 | 25 | 8,3401 | 7,7367 | 2291 |
| 2006-8 | 26 | 8,3655 | 8,3488 | 4225 |
| 2006-9 | 27 | 8,3891 | 8,5675 | 5258 |
| 2006-10 | 28 | 8,4109 | 8,6765 | 5864 |
| 2006-11 | 29 | 8,4309 | 8,6833 | 5904 |
| 2006-12 | 30 | 8,4491 | 8,7487 | 6303 |
| 2007-1 | 31 | 8,4655 | 8,7007 | 6007 |
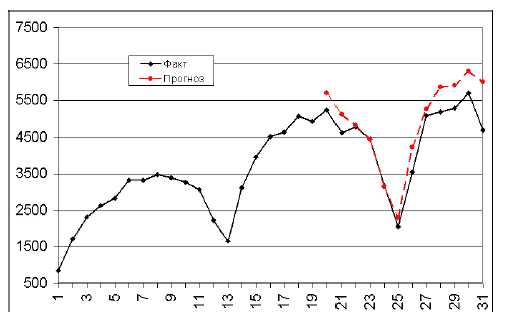
Рисунок 12 - Фактические данные и спрогнозированные. По оси X — номер периода.
Даже если модель очень хорошо описывает динамику реальных данных, что в общем-то большая редкость, то остаются еще шумы, которые вносят свою ошибку. Например, если уровень шума составляет 10% от значения показателя, то и ошибка прогноза будет не меньше 10%. Плюс, как минимум, еще несколько процентов ошибки добавятся из-за несоответствия модели и динамики реальных данных.
А вообще, лучший способ определить точность — это многократно делать прогнозы для одного и того же процесса и на основании такого опыта определять точность эмпирически.
| Период | № Периода | Факт | Прогноз | Ошибка, абс. | Ошибка, % |
| 2006-2 | 20 | 5233 | 5707 | 474 | 9 |
| 2006-3 | 21 | 4625 | 5119 | 494 | 11 |
| 2006-4 | 22 | 4776 | 4825 | 49 | 1 |
| 2006-5 | 23 | 4457 | 4441 | -16 | 0 |
| 2006-6 | 24 | 3169 | 3144 | -25 | -1 |
| 2006-7 | 25 | 2054 | 2291 | 237 | 12 |
| 2006-8 | 26 | 3549 | 4225 | 676 | 19 |
| 2006-9 | 27 | 5087 | 5258 | 171 | 3 |
| 2006-10 | 28 | 5187 | 5864 | 677 | 13 |
| 2006-11 | 29 | 5287 | 5904 | 617 | 12 |
| 2006-12 | 30 | 5700 | 6303 | 603 | 11 |
| 2007-1 | 31 | 4689 | 6007 | 1318 | 28 |
Заключение и список литературы
В этой статье мы рассмотрели сильно упрощенный метод прогнозирования. Тем не менее, при отсутствии резких изменений на рынке и внутри компании, даже такой простой метод дает удовлетворительную точность прогноза месяцев на 10 вперед.
Литература
1. Крамер Г. «Математические методы статистики».— М.: «Мир», 1975.
2. Кендэл М. «Временные ряды».— М.: «Финансы и статистика», 1981.
3. Андерсон Т. «Статистический анализ временных рядов».— М.: «Мир», 1976.
4. Бокс Дж., Дженкис Г. «Анализ временных рядов. Прогноз и управление».— М.: «Мир», 1976
5. Губанов В.А., Ковальджи А.К. «Выделение сезонных колебаний на основе вариационных принципов. Экономика и математические методы». 2001. т. 37. № 1. С. 91-102.