ПОСТРОЕНИЕ ПРОГНОСТИЧЕСКОГО КОМПЛЕКСА И ВНЕДРЕНИЕ ЕГО В ЭЛЕКТРОННУЮ СЕТЬ УНИВЕРСИТЕТА

Беловодский В.Н., Сивяков А.С.
Донецкий национальный технический университет г.Донецк
Кафедра компьютерных систем мониторинга

E-mail: arteom.sivyakov@gmail.com

Источник: Сборник материалов I всеукраинской научно-технической конференции студентов, аспирантов и молодых ученных «Информационные управляющие системы и компьютерный мониторинг (ИУС та КМ-2010)». – Донецк: ДонНТУ, 2010 – 634 с.

Аннотация

Беловодский В.Н., Сивяков А.С. Построение прогностического комплекса и внедрения его в электронную сеть университета. В докладе освещена идея построения прогностического комплекса, позволяющего проводить анализ временных характеристик основных метеопараметров. Изложена концепция его реализации и внедрения  в электронную сеть университета.

Актуальность. Адекватный (правдивый) прогноз погоды – это одна из важных современных проблем, имеющих практическое применение. Очень часто погодные условия становятся для людей бедственными. Однако мировая статистика показывает, что если доверять гидрометеорологической информации и адекватно на неё реагировать, то можно предотвратить от 30 до 40% потерь и полностью избежать человеческих жертв.

За последние десятилетия развитие идей и методов прогнозирования заметно продвинулось вперед, и этому способствовало как развитие математических подходов и усовершенствование методов исследования атмосферы, так и использование современной компьютерной техники.

Обзор предметной области исследования. Построение прогностической модели основано на обработке временных рядов, полученных  с метеостанции Vantage Pro 2, установленной на факультете КНТ ДонНТУ. Данная метеостанция позволяет снимать следующие данные:

• температура;
• влажность;
• давление;
• скорость ветра.

Все данные сохраняются на сервере кафедры КСМ и «АКИАМ». Интервал замеров составляет 10 минут. Таким образом, в процессе его эксплуатации постоянно формируется и постепенно накапливается совокупность временных рядов. Наличие этой информации делает вполне реальной  задачу разработки   прогностического комплекса.

В последние десятилетия в рамках нелинейной динамики получен ряд фундаментальных теоретических результатов и разработаны методики, обосновывающие принципиальную возможность прогнозирования физических процессов на базе их временных рядов. Теоретическим фундаментом  этих разработок  и методов является теорема Такенса [1]. Одной из его основополагающих идей  является то, что при построении эмпирических моделей по временному ряду в качестве недостающих переменных можно использовать или последовательные значения доступной наблюдаемой величины, или ее последовательные производные. Было доказано, что при реконструкции по скалярной временной реализации динамической системы и метод временных задержек, и метод последовательных производных гарантируют, что в новых переменных будет получено эквивалентное описание исходной динамической системы  при достаточно большой размерности восстановленных векторов D. А именно, должно выполняться условие D>2d, где d – размерность множества M в фазовом пространстве исходной системы, на котором происходит моделируемое движение. Эти утверждения и составляют содержание знаменитых теорем Такенса.

Анализ последних исследований. На данный момент на кафедре КСМ уже разработан прогностический комплекс [2]. Он позволяет на основе рядов, снимаемых с метеостанции ставить краткосрочные прогнозы температуры, влажности, давления и скорости ветра. Алгоритм работы комплекса разбивается на ряд следующих этапов:

- этап №1. Ряды снятые с метеостанции обрабатываются и систематизируются. После чего проводится их анализ с помощью визуального, спектрального и статистического методов, с целью выявления выраженных закономерностей, которые могли бы упростить выбор модельных уравнений;

- этап №2. Установление размерности модели, обеспечивающей однозначность прогноза. Проводится с использованием метода ложных соседей;

- этап №3.  Восстановление модельных уравнений осуществляется с использованием искусственных нейронных сетей, которые являются эффективным инструментом решения разнообразных задач и широко используются в последнее время для анализа временных рядов. Из большого числа существующих конфигураций нейронных сетей, с учетом их ориентации на классы решаемых задач и результатов предварительных экспериментов, в работе для реконструкции модельных уравнений были выбраны три типа сетей: однослойная линейная, двухслойная нелинейная и обобщенная регрессионная. Для расчета значений прогноза применяются различные прогностические схемы, основанные на итерировании базовых, и ансамблевые варианты.

Схематически этот алгоритм можно представить следующей схемой:

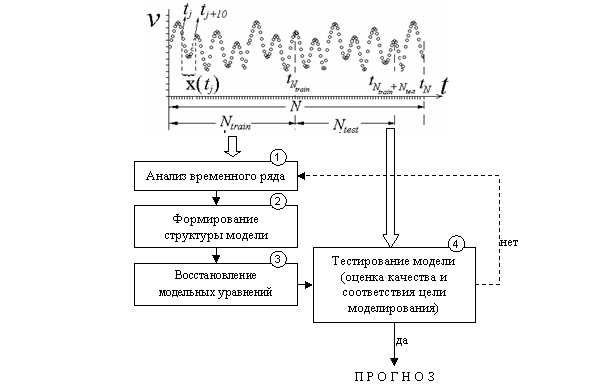
Рисунок 1 – Схема построения модели по временному ряду

Постановка задач. В процессе анализа разработанного прогностического комплекса и анализа литературных и интернет источников были сформулированы следующие задачи, которые требуют практического решения:

- работа прогностического комплекса и метеостанции должна быть синхронизированной и непрерывной;

- доступ к программной реализации комплекса должна быть скрыта от пользователя;

- метод ложных соседей необходимо заменить, наиболее популярным и современным методом работы с временными рядами и большими объемами данных;

- расширить инструментарий и обеспечить высокую интерактивность прогностического комплекса;

- доступ и анализ временных рядов должен производиться через электронную сеть университета, что обеспечит использование прогностического комплекса не только преподавателями, но и студентами.

Обоснование и пути решения выделенных задач. В качестве программных средств разработки используется среда Matlab, являющаяся высокоуровневым языком технических расчетов, интерактивной средой разработки алгоритмов и современным инструментом анализа данных. Эффективность Matlab обусловлена прежде всего ее ориентацией на матричные вычисления с программной эмуляцией параллельных вычислений и упрощенными средствами задания циклов. Удачно реализованы средства работы с многомерными массивами, большими и разреженными матрицами и многими типами данных.

Решение первой задачи осуществляется путем размещения на сервере кафедры КСМ базы данных, в которую постоянно бы происходило сохранение данных с метеостанции. Далее просто необходимо осуществить синхронизацию и взаимодействие  комплекса с базой данных. Эти задачи решаются с использованием инструмента Database математического пакета Matlab.

Вторая задача сводится к процессу компиляции проекта и собора необходимых .dll файлов в единую систему, которая в будущем получит название прогностический комплекс.

Идея использования вместо метода ложных соседей, метода главных компонент возникла в связи с тем, что  метод главных компонент (PCA) является  одним из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. PCA применяется во многих областях, таких как распознавание образов, компьютерное зрение, сжатие данных и т.п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных.

Четвертая задача решается путем внедрения в комплекс метода Эглайса, идея которого заключается в построении многомерного регрессионного уравнения [3]. Интерактивность увеличивается за счет усложнения диалога программы с пользователем.

Решение последней задачи сводится к следующей схеме.

Рисунок 2 – Схема работы прогностического комплекса

Выводы.В качестве основной задачи построения прогностического комплекса была принята задача усовершенствования и синхронизации прогностического комплекса с метеостанцией, а так же интеграция его в электронную сеть университета В результате работы был проведен анализ литературы по методам прогнозирования и оптимизации (сжатия) временных рядов. Был налажен сбор метеопараметров с локальной метеостанции, установленной в ДонНТУ,  показана возможность прогнозирования метеопараметров, с помощью методов реконструкции модельных уравнений, основанных на анализе временных рядов, сформулирована концепция работы прогностического комплекса в электронной сети университета.

Список литературы

1. Takens F. Detecting strange attractors in turbulence // Lec. Notes Math., 1981. V. 898. P. 366-381.

2. Гриценко А.В. Реконструкция уравнений и прогнозирование метеопараметров по их временным рядам. – Донецк, ДонНТУ, 2010. – 149 с.

3. Эглайс В.О. Аппроксимация табличных данных многомерным уравнением регрессии. – Вопросы динамики и прочности: Рига, 1981, Вып. 39. – с. 120-125.