Bukhalo Oleg, Klym Bogdan, Pochapsky Evgen, Mykytyn Galyna, Fedoriv Roman

Source of information: 15th World Conference on Non-Destructive Testing 15-21 October 2000 in Rome [Electronic resource] / NDT.net resource center, - access mode: http://www.ndt.net/article/wcndt00/papers/idn567/idn567.htm

Methods of acoustic emission (AE) signal analysis give an information about materials and constructions condition. For signal analysis the apparatus and program means are used for measuring amplitude, frequency, energetic, probability and other characters of the signal, which are connected with the defect characters.

So, for example, the length of crack jump is proportional to pulse amplitude, summary crack opening is proportional to a number of AE signal pulses [1], pulses amplitude distribution gives character of destruction type [2.. 4], position of the maximum and width of the frequency spectrum determine the stages of destruction [5], intensity of pulse flux define the kind of deformation [6], etc. For rise of reliability the space of signal signs is used. So, in [7] is proposed to use the position of dispersion ellipsis in median frequency -mean energy coordinates for cracks of normal alienation, longitudinal and transversal shear identification, in [8] the relative entropy - mean amplitude space is used for the nature of AE source in pipelines determination, in [9...11] corresponding signs spaces and complex parameters was used also.

In common case the AE signal X(t) may be offered in the form of pulse model

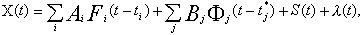
where A_i - maximum amplitude value of   i - th information pulse, F_i(.)- form- function and t_i- moment of pulse appearance, B_j, f _j(.),t_j^*- the same values for pulse noise component of the signal, S=S_°sinwt - continuous sine noise, where S_° - its amplitude, w - frequency,l (t) - continuous random noise, which may be described in correlation theory bounds.

In proposed model the first item is an information component, the others must be filtered or compensated.

Amplitudes and moments of pulse appearance have a random values, the sequence of information pulses is regarded as a Poisson flux. Thus information component of AE signal is characterized by amplitude distribution p(A), moments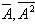entropy

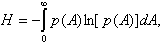
summary number N of pulses appeared during the time interval (t, t+Dt) with probability

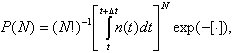
where n(t) - distribution parameter (flux intensity), pulse duration, its raising and fading times, number of oscillation in pulse, frequency spectrum F^*(w), where F^*(w) is Fourier transformation of F(t), spectral density

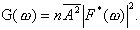
Removal of pulse noise component may be realized by form, duration or amplitude discrimination using program or apparatus means; by turning-off the measuring channel in the time of noise acoustic pulse (blows, mechanism working) expectation; by the basis and additional detector pulse signals coincidence (pulse electromagnetic hindrance); by removal the false pulses using mathematical treatment of time appearing difference (defects location) and by other methods.

Elimination of continuous sine noise may be realized by low-frequency filters; by using additional detector for noise registration and compensation; by feeding the inverse industrial net tension on an input of amplifier. Continuous random hindrance depends on amplifier noise, signals of radio stations, high- frequency electromagnetic noise and may be removed by using the additional detector, band and prognosis filters. The essence of prognosis filtration consists in prognosis values of random hindrance during pulse AE existence and compensation real hindrance by its prognosis values [12].
Amplitude distribution of signal information component is estimated by apparatus or program created multi channel amplitude analyzer. Then the histogram of amplitude distribution p(l), where l- number of analyzer's channel,

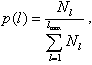
where N_l- summary amount of pulses, accumulated in l -th channel.

Then

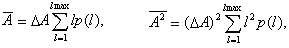
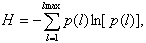
where DA- channel width and l_max- total amount of channels.

It is known [2...4], that on a different stages of destruction the pulse amplitude distribution transforms from normal (plastic deformation) to Rayleigh (micro crack appearance), exponential (crack growth) and Pareto (pre destruction stage). Then, if the kind of distribution law is known, method of maximum likelihood gives an opportunity to estimate the value of unknown parameter a of distribution by using the next formula

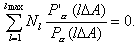
So, for example, for Rayleigh distribution

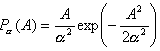
one has an estimation algorithm

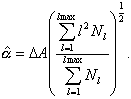
Estimation of an AE signal flux intensity is realized during the time of signal local stationarity, where n(t)=n= const. Then the maximum likelihood method for Poisson distribution with constant parameter gives an algorithm

where 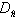- dispersion of estimation 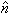, 1- time interval of local stationarity

Maximum of pulse flux intensity has place, as a rule, in a plastic deformation domain [1].

Stepped loading of a composit materials [13] or preliminary exposure of a specimens in a hydrogen atmosphere [14] give an exponential fading of intensity

where n₀ - initial value of intensity.

Then, using the multichannel time analizer with channel width DT, the a value may be determined by the equation [25]

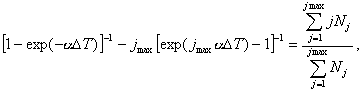
where N_j-amount of pulses, accumulated in j - th channel, j_max- total amount of channels.

Signal frequency characteristics are defined by Fourier transformation of F(t) function; pulse duration, its raising and fading times, amount of pulse oscillations measuring is not a difficult problem. Displacement of the frequency spectrum in low-frequency region shows the approaching to a critical point of a material destruction [5].

About mentioned and other algorithmes of the AE signal selection and processing are realized in information - measuring system destined for experimental materials researches, durability control, construction elements longevity, etc, with use of acoustic emission method. In his base lies registration by piezoelectric transformer of relisient waves, radiated by research object.

In composition of the system enter personal type computer, hardware part, beind the plates, inserted in standard computer slots, and also preliminary amplifiers of signals of piezoelectric transformers (PET).

On one plate are constructively placed two acoustic canals, containing each severally the modules of basic amplifier, analog - to -digital converter (ADC), operative information processing, lead-in-lead-out interface.

A measuring signal from each of PET acts over preliminary amplifier on amplifier module entrance of proper canal. Amplified in set frequencies band signal acts on the input of ADC and operative processing units and, then, personal computer.

Amplifier module contains a basic amplifier for signal amplification without diminution of signal to noise ratio, programme controlled filter for set of working frequencies band. ADC module provides an effective selection, minimizing a signal volume and deminishing a probability of false impulses registration, transformation of analog signal in real time scale with minimum distortions. In composition of this module also enters buffer memory.

A module of signal operative processing contains a device for determine the time of maximum signal appearance, device for intensity of pulse flux estimation, temporary marks generator, management scheme, comparator. Interface is destined for control by hardware block, and also for lead-in the measuring information from buffer memory ADC in the computer.

The system is provided by different means of program and manual control, permissive:

• to set the quantum frequency of ADC,
• to set the coefficient of signal amplification,
• to choose a working volume of buffer memory,
• to set a filter frequencies band,
• to set the system work condition: control, work,
• to choose a routine of an information lead-in in personal computer (parallel - succesive),
• to change program of a system synchronization routine (external or internal).

The system works in following routine:

• set of initial conditions,
• self-control of system functioning rightness in all,
• acoustic emission signal record in real time scale,
• processing of measuring information by definite algorithms and programs, as result of which one can estimate amplitude distribution and its parameters, distribution of spaces between contiguous pulses, define a frequency signal spectrum, autocorrelation function, coordinates of signal source,
• indication of registered AE signal and processing results.

Basic technical description

Working frequencies band 150-1000 kHz; maximum amplification coefficient 80 dB; step of amplification change 1 dB; brought to ADC input amplitudes discrimination threshold 100-2000 mV; brought to system entrance minimum impulses amplitude 10 mV; quantum ADC frequencies 2,4,6,8 MHz; discretization of ADC 8 bits; transformation time not more 0,1 ms; amount of decimal indication digits 5; volume of buffer memory 64 Kbytes.

Various methods for calibration and metrological providing of the measuring systems of the acoustic emission signals are used such as the methods of mechanical pendulum, self-mutuality at the wave guide, pulling down the graphite pivot or glass capillary, stream of sand, heat stroke, plate remagnetizing, brush circulation, metal globules fall, pivot measure, laser excitation and so on [15-20]. Such variety of the used methods is conditioned by impossibility of object standard model creation with the set values of parameters of acoustic emission, because consequently to the Kaiser's effect it impossible to obtain the AE signal in one model, even in the domain of elastic deformation. It is practically impossible to create a number of models with the same heterogeneity of crystalline grating, which will give the identical by characteristics signals of acoustic emission under the gauge load.

So, the calibration of measuring systems is realized not by changing the crystalline structure of standard model under load (that, in fact, causes the acoustic emission effect), but by action of physical fields (thermal, acoustic, magnetic, radiation, mechanical and so on), that causes the acoustic signals in the model without changing of its crystalline structure. Such change of the acoustic radiation source do not allow to obtain the real signal of acoustic emission, but it is practically justified. It is obviously, that in that case in the calibration mode, the signal at the output of piezoelectric source will differ by its parameters from the signal, appeared in real measuring situation.

The problem of apparatus metrological attestation (calibration) for measuring the AE signal parameters can be solved by another way on the base of each element testing principle. At the first stage, amplitude, frequency and another characteristics of piezoelectric converter are measured using the known methods [16-18]. On that base, the signal informative characteristics and parameters at the exit of converter and a range of theirs changes in real conditions of measuring are calculated or experimentally obtained.

Later the standard electric signal with the set with high accuracy values of informative parameters and statistical characteristics is modeled by electronic means using obtained results. This signal is used for testing the metrological characteristics of measuring systems. This gives the possibility, when investigated object is absent and without piezoelectric converter (its characteristics is defined a priori), to carry out the metrological attestation of measuring systems by the signal that imitates the real signal of acoustic emission for concrete measuring situation and has exactly known values of parameters (impulse form, flowing, duration, frequency spectrum) and statistical characteristics (distributions of impulses amplitudes, intervals between them and number of impulses, spectral density, correlation characteristics, distributions moments and so on). The mentioned values characterize the state of defects presence of investigated objects. [1]

Simplification of experimental equipment, possibility of change the standard signal in wide range of parameters and statistic characteristics, theirs high accuracy, possibility of signal repetition at experimental investigations, possibility of testing the metrological characteristics of measuring systems in the conditions, that are maximally fitted to real ones, cause the expediency of the presented approach.

In certain sense, the mentioned signals are the standard stochastic measure, with the parameters and statistical characteristics, that are constant or determined functions and provide the measure connection with the State Standard System.

Methods of stochastic standard signal generators application for testing the metrological characteristics of measuring systems are regarded in [21]. The transformation of pseudo - random numeric sequences with uniform distribution law into the numeric pseudo-random process with set characteristics using the universal Monte-Carlo and Neuman algorithms are putted at the base of the generator work. The shortcoming of Neuman algorithm - pseudo-random numbers realization in random moments of time, is compensated using method of decorrelation of the pointed sequence of pseudo-random numbers [22]. Than, the mentioned numeric process is transformed into electric signal using the digital - analog transformers and filters for giving the corresponding form to the impulses. Examples of organization of the generator structure is presented in [21,23].

The generators metrological providing is based on separate attestation of its digital and analog structure. Methods for metrological attestation of analog structure were considered in [24]. Attestation of the generator digital part used that fact, that pseudo-random process can be considered as determined one (when the generator structure is known and initial conditions are set), or as random one (using the generator as "black box" in the mode of signal generating). So, the statistic characteristics of the generated numeric signal are calculated on computer using the mathematical statistics methods proceeding from the generator known structure, and coincidence of algorithmic and real structure of the generator is defined by coincidence of determined planned numbers, computed a priori for the known initial conditions using computer. These numbers are used for periodical testing the generator and checking its ability to work.

REFERENCES

1. Bunina N.A. Research of a plastic deformation by an acoustic emission method. Leningrad State University, 1996.-156p.(in Russian).
2. Judin A.A., Ivanov V.I. To an acoustic emission theory in a metals plastic deformation. In coll. Acoustic emission of materials and constructions. Part 1 (1-st All-Union Conference). Rostov-na-Donu State University, 1989, pp.143-147 (in Russian).
3. Manohin A.I., Maslov N.I. Belov A.V. Energetic analisys of an acoustic signal nature. Ibid, p.p. 154-161 (in Russian).
4. Bujlo S.I. A statistic models using for a guantitative estimation of an acoustic emission signal amplitude distributions distortion and raise of trustworthiness AE method results. Defectoscopy,5, 1996, p.p. 26-34 (in Russian).
5. Lisak M.V., Skalsky V.R. A methodical approach to experimental acoustic emission estimation of crackfirmness of construction materials. Physico- Chemical Mechanics of Materials, 5, 1997, p.p. 17-30 (in Ukrainian).
6. Nondesrructive control. Book 2. Acoustic methods of control. Handbook/ Ermolov I.N., Aleshin N.P., Potapov A.I. M.:Visshaja shkola,1991.-283 p.(in Russian).
7. Muravin G.B., Simkin Ja.V., Merman A.I. Identification of material destruction mechanism by methods of acoustic emission signals spectral analisys. Defectoscopy, 4, 1989, p.p.8-15 (in Russian).
8. Bigus G.A., Dorokhova E.G. Identification of AE source on the base of an probability distribution of AE signal amplitude parameters. Technical diagnostics and nondestructive control, 3, 1998, p.p. 25-31 (in Russian).
9. Petersen T.B. Elaboration and using an automatical classification system for acoustic emission signals identification. Technical diagnostics and nondestructive control, 3, 1993, p.p. 3-9 (in Russian).
10. Novikov N.V., Filonenko S.F. Influence of an acoustic canal parameters on the criterial estimation of acoustic emission signal pick out. Technical diagnostics and nondestructive control,1, 1993,p.p. 47-51 (in Russian).
11. Nedoseka A.Ja., Fomichev S.K., Veligin V.A. Estimation of cracking degradation stages of low carbon steels welding junctions by acoustic emission method. Technical diagnostics and nondestructive control, ;3, 1993, p.p. 17-21 (in Russian).
12. Bukhalo O.P. Suppression of continuons hindrances in transmission channels of pulse stochastic signals. Metrology, 6, 1990, p.p.11-19 (in Russian).
13. Nadolinny B.A., Tikhij V.G., Sanin F.P. AE method of composit materials destruction prognosis. In coll. Acoustic emission of materials and constructions. Part 2 (1-st All-Union Conference). Rostov-na -Donu State University. 1989 p.p.101-105 (in Russian)
14. Lisak M.V., Skalsky V.R., Vainman A.B., Sergienko O.R. Estimation of boiler pipes steels hidrogen degradation by pulse sounding. Technical diagnostics and nondestructive control, 3, 1993, p.p. 58-65 (in Russian).
15. Tutnov A.A., Tutnov I.A., Chuvarin A.N. Diagnostics of materials destruction on the base of acoustic emission signal form analysis. In coll. Acoustic emission of materials and constructions. Part 1 (1-st All-Union conference). Rostov-na-Donu State University, 1989, p.p.59-63 (in Russian).
16. Tripalin A.S. Main directions of acoustic emission signal convertors creation and improvement. Ibid, p.p. 69-76 (in Russian).
17. Gorlitsin N.V., Gabitenko N.K., Kolitenko N.A. Method of estimation and analysis of piezosensors amplitude-freguence characteristics and its direction diagrams. Ibid, p.p. 81-86 (in Russian).
18. Sosedov V.R., Melkanovich A.F. Detkov A.Ju. Research of acoustic emission convertors parameters. Ibid, p.p. 76-81 (in Russian).
19. Ivanov V.I., Mirgazov V.A. Rerearch of acoustic emission imitators. Technical diagnostics and nondestructive control, 3, 1993, p.p. 47-51 (in Russian).
20. ASTM-E 1106-86. Standart method for Primary Calibration of Acoustic Emission Sensors, 1986.
21. Bukhalo O.P. Application, reproduction and certification of a model pulse stochastic signal. Measuring technique, 6, 1997, p.p.24-44 (in Russian).
22. Bukhalo O.P. Generation of pseudorandom numbers stochastic seguences. Metrology, 1, 1987, p.p. 3-9 (in Russian).
23. Bukhalo O.P. Generator of nonstationary Poisson pulse signal. Measuring technique,4, 1998, p.p.13-17 (in Russian).
24. Bragin A.A., Semeniuk A.L., Borodaty V.N. Automatical control of ADC and DAC. Measuring techninque, 4,1979,p.p.25-26(in Russian).
25. Bukhalo O.P. Estimation of the exponentially damping nonstationary Poisson flux parameters. Measuring techninque, 2,1994,p.p.57-59 (in Russian).