Автор: С.А. Поттосина, В.А. Журавлев

Источник: Мн.: БГУИР, 2003. – 94 с.

Для обеспечения качества модели необходимо, чтобы было n > 3k, где n – количество наблюдений, k – количество факторов. Модель множественной регрессии оценивается с помощью следующих критериев:

1. Коэффициент детерминации (R²):

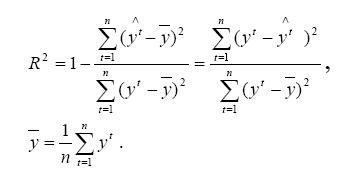
Всегда 0 < R² < 1. Чем ближе R² к 1, тем точнее модель. Если R² > 0,8, то модель считается точной, если R² < 0,5, то модель надо улучшить, либо выбрав другие факторы, либо увеличив количество наблюдений.

2. Коэффициент множественной корреляции:

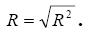
3. Скорректированный коэффициент детерминации:

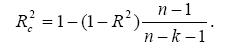
4. Стандартная ошибка:

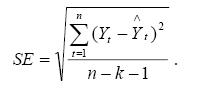
5. Оценка значимости модели, т.е. оценка того насколько верна гипотеза о линейности регрессии между Y и факторами Xi осуществляется по F-критерию Фишера. По наблюдаемым значениям определяется значение

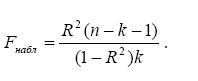
Если Fнабл > Fкр = Fтабл(0,95; n – 1; n – k – 1), где 0,95 – уровень доверительной вероятности, (n – 1) и (n – k – 1) степени свободы модели, то модель считается значимой, и принимается гипотеза о линейной регрессии между переменными Y и Xi, где Fтабл – табличное значение F-критерия Фишера.

Иначе гипотеза о линейной регрессии отвергается и надо изменять модель: выбрать другие факторы, увеличить количество наблюдений или построить нелинейную регрессию.

6. Оценка значимости коэффициентов регрессии (кроме свободного члена) осуществляется сравнением статистики

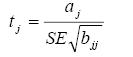
с табличным значением t-статистики Стьюдента. В bjj – диагональный элемент матрицы (Х^Т*Х)^–1. Если значение превосходит табличное значение t-статистики Стьюдента, то j-й коэффициент считается значимым, в противном случае фактор, соответствующий данному коэффициенту следует исключить из модели.

7. Доверительный интервал для прогнозных значений линии регрессии определяется по формуле

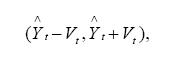
где

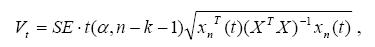
t(a,n-k -1) табличное значение критерия Стьюдента при заданном уровне значимости α и числе степеней свободы (n – k – 1);

хn(t) – вектор-столбец факторов для прогнозных значений времени (t = n + 1, n + 2, n + 3, …).

Матрица (Х^Т*Х)^{–1 соответствует наблюдаемым значениям факторов.}

8. Влияние факторов Х на показатель Y оценивается с помощью коэффициентов эластичности Эj и бета-коэффициентов:

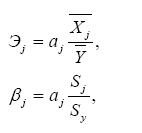
где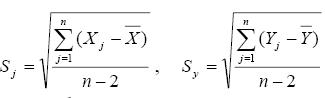– несмещенные среднеквадратичные отклонения факторов Х и Y.

Коэффициенты эластичности Эj показывают, на сколько процентов изменится значение переменной Y при изменении Хj на 1%. Бета- коэффициенты βj показывают, на какую часть среднеквадратичного отклонения изменится Y при изменении Хj на величину своего среднеквадратичного отклонения.

Долю влияния j-го фактора в суммарном влиянии всех факторов на показатель Y оценивают с помощью дельта-коэффициентов:

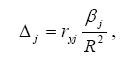
ryj – коэффициент корреляции между j-м фактором и переменной Y. При k = 1 получаются оценки для модели простой (однофакторной) регрессии.

Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997.

Экономико-математические модели и методы / Под общей ред. А.В. Кузнецова. – Мн.: БГЭУ, 2000.

Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2001.