Источник: http://www.victoria.lviv.ua/html/oio/html/theme11_1_rus.htm#11_8
При описании объектов и явлений с помощью нечетких множеств используется понятие нечеткой и лингвистической переменных.
Нечеткая переменная характеризуется тройкой <α, X, A>, где
α — имя переменной,
X — универсальное множество (область определения α),
A — нечеткое множество на X, описывающее ограничение (то есть m A(x)) на значение нечеткой переменной α.
Лингвистической переменной называется набор <β,T,X,G,M>, где
β — имя лингвистической переменной;
Т — множество его значений (терм-множество), представляющие имена нечетких переменных, областью определения, которых является множество X. Множество T называется базовым терм-множеством лингвистической переменной;
G — синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество T∩G(T), где G(T) — множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
М — семантическая процедура, позволяющая преобразовать новое значение лингвистической переменной, образованной процедурой G, в нечеткую переменную, то есть сформировать соответствующее нечеткое множество.
Во избежание большого количества символов:
символ β используют как для названия самой переменной, так и для всех его значений;
для обозначения нечеткого множества и его названия пользуются одним символом, например, терм «молодой», является значением лингвистической переменной β = «возраст», и одновременно нечетким множеством М («молодой»).
Присваивание нескольких значений символам предполагает, что контекст допускает неопределенности.
Пример
Пусть эксперт определяет толщину изделия, с помощью понятия «маленькая толщина», «средняя толщина» и «большая толщина», при этом минимальная толщина равняется 10 мм, а максимальная - 80 мм.
Формализация этого описания может быть проведена с помощью лингвистической переменной <β,T,X,G,M>, где
β — толщина изделия;
T — {«маленькая толщина», «средняя толщина», «большая толщина»};
X — [10, 80];
G — процедура образования новых термов с помощью связок «и», «или» и модификаторов типа «очень», «не», «слегка» и др. Например, «маленькая или средняя толщина», «очень маленькая толщина» и др.;
М — процедура задания на X = [10, 80] нечетких подмножеств А1=«маленькая толщина», А2 = «средняя толщина», А3=«большая толщина», а также нечетких множеств для термов из G(T) соответственно правилам трансляции нечетких связок и модификаторов «и», «или», «не», «очень», «слегка».
Вместе с рассмотренными выше базовыми значениями лингвистической переменной «толщина» (Т={«маленькая толщина», «средняя толщина», «большая толщина»}) существуют значения, зависящие от области определения Х. В данном случае значения лингвистической переменной «толщина изделия» могут быть определены как «около 20 мм», «около 50 мм», «около 70 мм», то есть в виде нечетких чисел.
Функции принадлежности нечетких множеств:
«маленькая толщина» = А1 , «средняя толщина»= А2, «большая толщина»= А3.
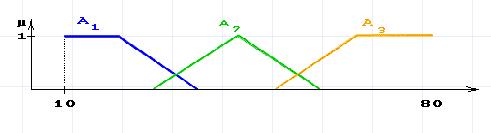
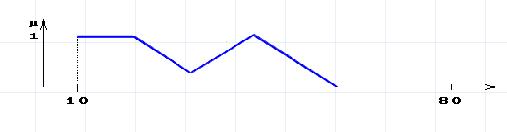
Функция принадлежности:
нечеткое множество «маленькая или средняя толщина» = А1∩А1.
Преимущества нечетких систем
Коротко перечислим преимущества fuzzy-систем по сравнению с другими:
- возможность оперировать нечеткими входными данными: например, непрерывно изменяющиеся во времени значения (динамические задачи), значения, которые невозможно задать однозначно (результаты статистических опросов, рекламные компании и т.д.);
- возможность нечеткой формализации критериев оценки и сравнения: оперирование критериями «большинство», «возможно», «преимущественно» и т.д.;
- возможность проведения качественных оценок как входных данных, так и выходных результатов: вы оперируете не только значениями данных, но и их степенью достоверности (не путать с вероятностью!) и ее распределением;
- возможность проведения быстрого моделирования сложных динамических систем и их сравнительный анализ с заданной степенью точности: оперируя принципами поведения системы, описанными fuzzy-методами, вы во-первых, не тратите много времени на выяснение точных значений переменных и составление описывающих уравнений, во-вторых, можете оценить разные варианты выходных значений.