Перевод: Снежок К.В.
Источник:http://www.docstoc.com/docs/21399212/A-Linear-Regression-Model-for-Real-Estate-Pricing
1. Введение
Этот проект предназначен для оценки модели линейной регрессии, используя реальные данные. Существует два метода оценки недвижимого имущества: сравнение продаж и метод определения доходов. Сравнение продаж оценивает недвижимое имущество, опираясь на цены сравнимого имущества. В связи с тем, что этот подход допускает, что недвижимое имущество с похожими характеристиками имеет одинаковую стоимость, то естественно использовать модель линейной регрессии, чтобы воплотить этот метод в практику. Тем не менее, неизвестно какие свойства недвижимости должны быть взяты в оценочной модели. Мы будем опытным путем анализировать значимость нескольких независимых переменных к стоимости недвижимости. Кроме того, проверим достоверность модели линейной регрессии.
2. Данные
Данные взяты из книги Статистический метод в бизнесе и экономике, написанной Линдом, Маршалом и Мэйсоном. Она содержит 105 цен продаж и несколько ключевых характеристик имущества, основанных на информации о продажах домов в Венеции, Флориде в 1995 году.
Зависимая переменная – это цена дома в тысячах долларах. Объекты с зависимой переменной следующие:
Апартаменты с кол-ом спален: количество спален
Размер:- Размер дома в футах
Басс: - Наличие бассейна (1 = да, 0 = нет)
Рас: - Расстояние от центра города в милях
Город:- Размер города (шифр 1-5)
Гараж:-Наличие гаража (1 = да, 0 = нет)
Ванная:-Кол-во ванных комнат
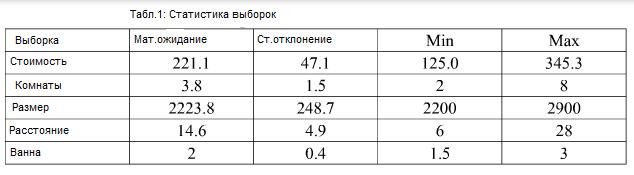
Описательная статистика непрерывных переменных представлена в таблице 1. Можно увидеть, что цена и размер имеют довольно большую шкалу, которая показывает нам логарифм двух переменных в регрессии.
Мы видим слабую линейную связь между некоторыми парами. Тем не менее, этого предварительного анализа не достаточно, чтобы определить соответствие независимых переменных к стоимости дома.
3. Эмпирический результат
a. Основные результаты метода наименших квадратов
Мы используем этот метод для оценки линейной регрессионной модели с 7 независимыми переменными. Только 100 измерений использовались для оценки. Остальные 5 оставлены с целью прогноза. Оценочная модель выглядит следующим образом:
цена = 65.07 + 7.60 • комнаты + 0.03 • размер -19.8 • бассейн -1.37 • расстояние - 0.93 • город + 37.9 • гараж + 28.4 • ванная
R-квадрат регрессии 61.4%, что означает довольно хорошую пригодность модели для данных. Оценки обычного метода наименьших квадратов, стандартные ошибки, Т-статистика и Р-значения представлены в таблице 2.
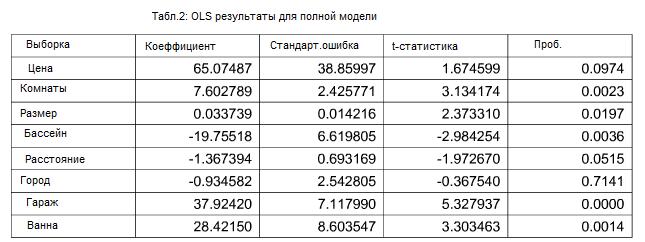
Город показывает совершенно незначительную величину 0.71. Результат не значит, что местность здания не имеет значения для стоимости дома, т.к. расположение должно приниматься как абсолютная переменная, а не как числовая переменная. Если мы берем фиктивные переменные, чтобы обозначить абсолютную величину Город, то возможно, что некоторые фиктивные переменные станут статистически значи кроме мы. Расстояние почти несущественно, 5%. Все остальные переменные статистически важны, кроме отрезок между двумя точками.
Основываясь на t-критерии, мы исключаем Город и Расстояние из модели. Но оставляем постоянный терм, потому что оценка отсекаемого отрезка сравнивается с постоянными величинами, и это неправильно иметь линейную модель без постоянного терма. Мы дополняем регрессию новыми независимыми переменными. Результаты обычного метода наименьших квадратов представлены в таблице 3. Новая модель рассчитывается по формуле:
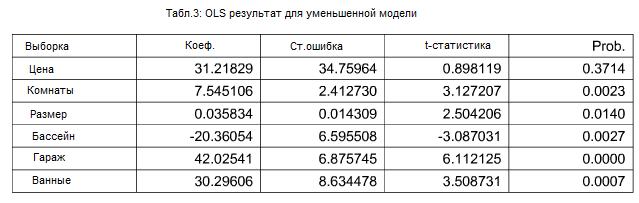
цена = 31.22 + 7.55• комнаты + 0.04 • размер - 20.36 • бассейн + 42.03. • гараж + 30.30 ванна
t-критерии показывают, что все независимые переменные, кроме отсекаемого отрезка, статистически значимы, даже при 1%. F критерий также показывает, что уравнение регрессии статистически значимо на любом принятом уровне. R-квадрат на отметке 60% и немного понизился.
Отметим интересное наблюдение о пояснении коэффициентов в модели. Приемлемая оценка выводится для всех коэффициентов кроме бассейна. Оценочный коэффициент для бассейна -20, тем самым модель предполагает, дом с бассейном имеет стоимость ниже на $20, 000, чем дом без бассейна и с тем же условиями. Будет слишком неосторожно заявить, что бассейн обычно негативно влияет на стоимость дома. Возможно, результат можно объяснить с помощью особенных предпочтений в этом районе. Тем не менее, этот необычный результат заставляет нас задуматься о действенности примера.
b. мультиколлинеарность
Мы хотим проверить, существует ли мультиколлинеарность в независимых переменных. Самая высокая корреляция 41% между Комнатами и Размером. Мы приходим к заключению, об адекватности мультиколлинеарности в данных.
c. функциональная форма модели
Мы обнаружили, что Цена и Размер имеют довольно большие величины по сравнению с другими переменными. Поэтому можно предположить, что у них логарифмическая форма. Мы запускаем новую регрессию, в которой независимая переменная в уравнении регрессии Размер заменяется логарифм log(size). Результаты оценки обычного метода наименьших квадратов показаны в таб.4. R-квадрат новой модели равен приблизительно 60%, даже немного ниже, чем в первоначальной модели. Можно отметить, что Расстояние значительно на 5% уровне в этой модели. Статистическая значимость независимых переменных остается практически неизменной. Не произошло идеального совпадения, изменив функциональную форму модели. Пояснение коэффициентов в этой модели с помощью логарифмов не наглядна. Поэтому мы будем придерживаться сведенной линейной модели в (а).

d. гетероскедастичность
Необходимо проанализировать остальные данные обычного метода наименьших квадратов и проверить возможную гетероскедастичность для относящимся к различным областям данные. Мы считаем подобранные величины Цены и остальные данные обычного метода наименьших квадратов. После мы сортируем остальные данные к подобранным величинам Цены и строим диаграмму рассеивания относительно подобранных величин, рис.2. Наблюдаем, что все элементы точно распределены и нет очевидных примеров для подчинённого положения остальных данных к подобранным.
Иногда недостаточно графика остатков, чтобы определить гетероскедастичность. Более того, мы провели White тест гетероскедастичности на остатках обычного метода наименьших квадратов. F критерий 1.23 и связанный с ним p-критерий 0.29, а n*R-квадрат 9.75, связанный p-критерий 0.28. Оба результата отрицают гипотезу гетероскедастичности на обычном уровне. Подведя итог, можно сказать, что линейная модель с гомоскедастической ошибкой нормальна для таких данных.
e. Образей прогноза
Мы можем оценить достоверность этой линейно модели регрессии с помощью проверки точности прогноза. Оцениваем линейную модель с помощью 100 и 105 показаний данных. Мы прогнозируем цены для остальных 5 показателей, сравниваем реальные значения и прогнозируемые значения 5 стоимостей. Для того, чтобы сделать наши наблюдения более объективными, мы также описываем 95% интервала доверия для 5 прогнозируемых цен. Видим, попадает ли истинное значение в интервалы. Прогнозируемые результаты показаны на рисунке. Мы можем увидеть, что прогнозы вне наших примеров неплохие. 4 из 5 истинных величин попали в 95% интервал доверия .Одно показание за пределами интервала также возле нижнего предела. Прогнозируемые величины довольно близки к истинным величинам по сравнению с интервалом доверия.

4. Вывод
В этом проекте мы предложили линейную модель регрессии, чтобы определить цену дома, используя ключевые характеристики недвижимости. Используя массив реальных данных с 100 показателями мы дали оценку модели по обычному методу наименьших квадратов. Мы исключили 2 неважные независимые переменные, основываясь на t тесте. Наши результаты в мультиколдинеарности, гетероскедастичности и функциональной форме показывают, что линейная можель регрессии с гомоскедастичными ошибками является нормальной для такого множества данных. Результаты прогнозирования показали, что модель строится успешно в прогнозировании. Интересное наблюдение в этом проекте заключается в том, что результат оценки влияния бассейна на стоимость дома протеворечит нашим ожиданиям. Причина все еще неизвестна.