Автор: Петровский А.Б.

Источник: М.: Едиториал УРСС,2003. – 248 с.

Процедура классификации объектов в рамках формальной логики может быть описана как совокупность (последовательность) решающих правил, которые представляются выражениями вида:

При прямой классификации терм [условия] включает названия объектов или перечень значений признаков, описывающих объекты класса, что часто считается эквивалентным. При непрямой классификации один или несколько термов [условия] конструируются как отношения между различными признаками и/или их значениями. Терм [решениe] в обоих случаях означает, что объект принадлежит к определенному классу. Заметим, что подобным образом формируются и базы знаний экспертных систем продукционного типа.

При достаточно небольшом числе классифицируемых объектов и признаков, их описывающих, семейство решающих правил легко обозримо и доступно для анализа. Чем больше количество рассматриваемых объектов и разнообразнее решающее правила их классификации, тем труднее становится анализ этих правил. Могут существовать различные причины, обусловливающие неоднозначность классификации, к примеру, если объекты сортируются разными экспертами. Эксперты могут относить сильно различающиеся объекты в один и тот же класс, а объекты со сходными значениями признаков – в разные классы. Несогласованность индивидуальных решающих правил может быть вызвана неоднозначностью понимания экспертами решаемой задачи, ошибками или неточностями, допущенными экспертами при первоначальной классификации объектов, субъективным различием решающих правил, используемых разными экспертами, специфичностью знаний самих экспертов, нетранзитивностью отдельных экспертных суждений и многими другими причинами.

В итоге могут появиться решающие правила, среди которых будут одинаковые, сходные, различающиеся и противоречивые правила. В этом случае возникает проблема: построить такое обобщенное решающее правило или небольшую группу правил, которые наилучшим (в некотором смысле) образом аппроксимируют совокупность всех индивидуальных правил сортировки объектов, включают минимальный набор признаков и относят объекты в заданные классы с допустимой точностью

Итак, процедура построения обобщенного решающего правила для классификации многопризнаковых объектов включает следующие основные этапы.

Шаг 1. Построить таблицу решений C=||kAi(xj)||k×h для рассматриваемой совокупности многопризнаковых объектов A ={A1,...,Ak}, строки которой соответствуют мультимножествам Ai вида

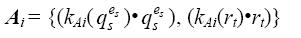
Шаг 2. Объединить объекты Ai, относящиеся к заданным классам Xa и Xb, воспользовавшись формулами

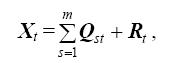
Получить преобразованную таблицу решений C’=||kXt’(xj)||2×h, строки которой соответствуют мультимножествам Xa и Xb.

Шаг 3. Решить задачу оптимизации

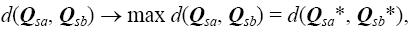
для каждого бинарного разложения {Qsa*, Qsb*} по s-ой группе признаков Qs и найти аппроксимирующий признак qs* в каждом s-ом блоке преобразованной матрицы C’.

Шаг 4. Проранжировать аппроксимирующие признаки qs* по убыванию величины расстояния d*=d(Ra, Rb) или показателя точности ρs .

Шаг 5. Выбрать аппроксимирующие признаки qs*, которые обеспечивают необходимую точность аппроксимации ρs>0, и сформировать из них обобщенное решающее правило для классификации многопризнаковых объектов.

Упорядочение объектов.

Еще одним весьма распространенным подходом к структуризации совокупности объектов A={A1,...,Ak} является их строгое или нестрогое упорядочение, которое представляет собой введение между объектами бинарных отношений строгого или нестрогого порядка, эквивалентности или несравнимости, заданных на множестве свойств объектов. Сравнение объектов по их свойствам производится на основе признаков, характеризующих объекты.

К числу наиболее популярных методов упорядочения объектов относятся непосредственная порядковая классификация, ранжирование, парные сравнения. Многие задачи принятия решений часто сводятся именно к ранжированию объектов, где итоговое упорядочение ищется либо на основе свойств объектов, либо исходя из предпочтений ЛПР, либо на сочетании того и другого.

Представим рассмотренную процедуру упорядочения совокупности многопризнаковых объектов в виде следующего алгоритма

Шаг 1. Вычислить для каждого объекта Ai из совокупности A ={A1,...,Ak} взвешенную сумму всех первых (наилучших) оценок по всем критериям Qs и упорядочить объекты от лучшего к худшему по величинам Sai сумм первых оценок. Если найдутся группы эквивалентных или несравнимых объектов Ai1,…,Ait, имеющих одинаковые суммы Sai , перейти к шагу 2.

Шаг 2. Вычислить для каждого объекта Air, r=1,…t в соответствующей группе взвешенную сумму 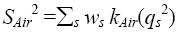всех вторых оценок по всем критериям Qs и упорядочить объекты внутри каждой группы от лучшего к худшему по величинам Sair сумм вторых оценок. Если останутся подгруппы эквивалентных или несравнимых объектов Airu,…,Airv, имеющих одинаковые суммы Sair, перейти к шагу 3

Шаг 3. Вычислить для каждого объекта Airp в соответствующей подгруппе взвешенную сумму всех третьих оценок по всем критериям Qs и упорядочить объекты внутри каждой подгруппы от лучшего к худшему по величинам сумм SAirp третьих оценок. Продолжить процедуру до полного упорядочения всех объектов из совокупности A ={A1,...,Ak}. Если число hs значений оценок es qs у некоторых критериев Qs окажется меньше требуемого на данном b-ом шаге алгоритма, то следует считать kAir…p(qs b)=0.

Проблемы классификации и упорядочения объектов, которые описываются многими количественными и качественными признаками, причем каждый из объектов может существовать в нескольких различающихся «экземплярах», являются достаточно трудными. Эти трудности имеют и содержательные основания (например, некорректность применения процедур «усреднения» качественных признаков), и формальные причины (например, большая размерность задачи). Главные из перечисленных трудностей оказалось возможным преодолеть благодаря использованию нового теоретического инструментария, основанного на понятии мультимножества. Применение теории мультимножеств позволяет разрабатывать новые подходы к решению новых классов задач, новые методы анализа и обработки данных и знаний, которые не содержат необоснованных преобразований и не приводят к потере или искажению исходной информации.

Теория мультимножеств и практика их применения находятся еще только в начале своего развития. Однако, несмотря на недостаточную «зрелость» теоретических разработок, мультимножества уже успешно используются в различных приложениях, в частности, в многокритериальном анализе слабо формализованных проблем и принятии решений, теории сетей Петри, моделировании и анализе сложных систем, распознавании образов, искусственном интеллекте, теории формальных языков, математическом программировании, методах обработки разнородной информации и так далее. И здесь, и в других областях можно ожидать появления многих новых и интересных результатов.

A.B.Petrovsky. Multiattribute sorting of qualitative objects in multiset spaces.// M.Koksalan, S.Zionts (Eds.). Multiple Criteria Decision Making in New Millennium. – Springer-Verlag, Berlin, 2001, 124-131.

A.B.Petrovsky. Constructing a general decision rule for contradictory expert classification of 237 multiattribute objects.//Pattern Recognition and Image Analysis, 2001,V.11,№1,73-76.

A.Petrovsky. Method for approximation of diverse individual sorting rules.//Informatica, 2001, V.12, №1, 109-118.

A.Petrovsky. Multiple criteria project selection based on contradictory sorting rules.// M.Goldevsky, H.Mayr (Eds.). Information Systems Technology and its Applications. – Gesellschaft fur Informatik, Bonn, 2001, 199-206.

А.В.Литвинова. Упорядочивание многопризнаковых объектов на основе теории мультимножеств.//Дипломная работа на соискание степени магистра. Московский физико- технический институт (государственный университет), М., 2002.

Л.Г.Евланов. Теория и практика принятия решений. – М.: Экономика, 1984.