РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ И ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В МИКРОПРОЦЕССОРНОЙ СИСТЕМЕ УПРАВЛЕНИЯ ПРИВОДОМ НАЖИМНОГО УСТРОЙСТВА ПРОКАТНОГО СТАНА

Стародубцев Д.Н., Губарь Ю.В.

Донецкий национальный технический университет

Источник: Информатика и компьютерные технологии — 2008 / Сборник трудов 4 международной научно-технической конференции студентов, аспирантов и молодых учёных. — Донецк, ДонНТУ — 2008, с. 416-418.

В докладе рассматриваются актуальные вопросы разработки и исследования средствами системы Matlab цифроаналоговой системы с комбинированным управлением приводом нажимного устройства прокатного стана.

Введение

Позиционные электроприводы нажимных винтов (НВ) обжимных прокатных станов работают в напряженном повторно-кратковременном режиме. Задача привода состоит в том, что он перемещает рабочий орган механизма из одного фиксированного положения в другое по программе, которая определена требованиями технологического процесса. Для достижения высокой производительности таких приводов необходимо повышать их быстродействие [1].

Комплексная автоматизация оборудования и повышение требований по точности регулирования положения вызывают необходимость широкого внедрения микропроцессорных систем, использующих цифровые способы обработки информации. Это приводит к дискредитации процесса регулирования и существенно усложняют анализ и синтез таких систем.

Целью данной работы является разработка средствами системы Matlab и пакета моделирования Simulink [2] цифроаналоговой модели системы регулирования положения (СРП) нажимными винтами прокатного стана и исследование динамических процессов в рассматриваемой системе.

1. Описание объекта исследования

Микропроцессорная система управления приводом НВ выполнена по принципу подчиненного регулирования. Она включает аналоговые контуры регулирования тока (КРТ) и скорости (КРС) и цифровой контур положения (КРП) с линейным регулятором положения (РП). На входе РП установлен цифровой задатчик положения (ЦЗП), который с периодом квантования по времени Т формирует технически оптимальный по быстродействию закон изменения регулируемой координаты (угла поворота вала двигателя 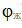), а также сигналы компаундирующих связей, пропорциональным желаемым законам изменения скорости и ускорения . 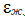Сумма этих сигналов представляет управляющее воздействие G, которое подается на вход РП:

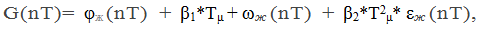
где 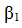и — коэффициенты компаундирующих связей ЦЗП; 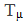— малая некомпенсированная постоянная КРТ.

В качестве датчика скорости применен тахогенератор. Для измерения положения (угла поворота вала двигателя) используется кодовый датчик типа КД-3-ТВ2. Двигатель постоянного тока питается от управляемого тиристорного преобразователя.

Величины заданных перемещений хранятся в блоке памяти микроЭВМ, на которую возлагаются функции ЦЗП и РП. Согласование цифрового РП с аналоговым КРС осуществляется преобразователем код-напряжение (ПКН).

2. Описание модели СРП

На рис. 1 приведена модель СРП в блоках пакета Simulink.

Рис. 1 — Модель цифроаналоговой СРП с комбинированным управлением

Аналоговый КРТ представлен на рисунке в свернутом виде и имеет передаточную функцию

Коэффициенты усиления регуляторов скорости (PC) K4 и положения (РП) К3 настроены в соответствии с требованиями модульного оптимума (МО) [3]. Временная задержка t3, вызванная работой микроЭВМ при реализации алгоритмов ЦЗП и РП, отражена блоком Delay1. Связь аналоговых и цифровых контуров регулирования в модели осуществляется с помощью экстраполяторов нулевого порядка Е1 и Е2, которые фиксируют текущие значения координат на период дискретности Т. Текущие значения координат тока i(t), скорости 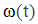и угла поворота вала двигателя 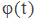через выходные порты Out выводятся в рабочую область Matlab и далее отражаются графически.

3. Анализ результатов моделирования

Экспериментальные исследования подтвердили работоспособность разработанной модели. В качестве примера на рис. 2 в относительных величинах приведены диаграммы переходных процессов в СРП при отработке больших перемещений (скорость двигателя изменяется при этом по трапецеидальной диаграмме).

Анализ результатов моделирования показал, что при выборе параметров системы (К3,К4, 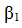, ) из условий МО, перерегулирование по току на всех участках движения привода составляет 4 — 6 %. При отсутствии корректирующих связей ( 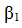= = 0) быстродействие системы снижается с увеличением периода квантования Т и временного запаздывания t3.

Использование корректирующих связей позволяет скомпенсировать дополнительную инерционность системы, обусловленную эффектом квантования и запаздывания, и повысить быстродействие привода. Так, например, время tc первого согласования тока с установившимся значением в комбинированной СРП в два раза меньше по сравнению с системой, работающей только по отклонению, и близко к значению, полученному в аналогичной непрерывной системе. Это имеет большое практическое значение для увеличения производительности НВ прокатного стана.

Рис. 2. Графики переходных процессов

4. Выводы

В системе Matlab разработана и проверена цифроаналоговая модель СРП с комбинированным управлением по задающему воздействию для управления нажимными винтами прокатного стана. Использование принципа комбинированного управления позволяет улучшить динамические свойства СРП и повысить производительность привода нажимных винтов прокатного стана.

Литература

[1] Бычков В. П. Электропривод и автоматизация металлургического производства. — М.: Высшая школа, 1977.— 391с.

[2] Hoffman J. MATLAB and SIMULINK. Beispielorientirte Emfuhrung in Simulation dynamischer Systeme. — Bonn: Addison — Wesley — Longman, 1998 — 493 s.

[3] Коцегуб П. Х., Губарь Ю. В. Упрощенный синтез дискретных систем управления по модульному оптимуму. — Известия вузов. Электромеханика, 1989, № 3, с. 68-73.