Simplified Watershed Transformation

ABSTRACT

The watershed transformation is the primary tool of Mathematical Morphology for image segmentation. However,
the resulting image often appears over segmented into a large number of tiny regions (basins), most of which are not significant in the problem of domain. In this paper, a method is proposed which makes use of opening closing filter in morphological reconstruction and webber principle.
Keywords: Mathematical Morphology, watershed transformation

1. INTRODUCTION

The segmentation of an image can be defined as its partition into different regions, each having certain
properties. Uniformity criteria such as homogeneous grey level distributions are generally used to group
pixels into regions [3]. However, the number of regions produced may be too large, and most of them are likely to be perceptually insignificant; it is then necessary to reduce the total number of regions.
Watershed is an algorithm for image segmentation developed in recent years based on mathematical morphology [1], and has draw great attention for its fast computing and high accuracy in locating the weak edges of adjacent regions. But classical watershed segmentation is sensitive to noise and can leads to serious oversegmentation.
In this paper, we propose segmentation in the framework of Mathematical Morphological opening-closing filtering and webber principle. [9], and discuss a method to reduce over segmentation.
The application of this method for segmenting image overcomes over-segmentation effectively, and produces
a satisfactory Segmentation result apparently superior to the approach of employing watershed. Correct
segmented results are very useful for the image analysis, prediction and diagnoses.

2. WATERSHED TRANSFORMATION

The watershed method also called, as watershed transformation is a region-based segmentation method based on the mathematical morphology. In geography, a watershed is the ridge that divides areas drained by different river systems. By viewing an image as a geological landscape, the watershed lines determine the boundaries that separate image regions. In the topographic representation of an image I, the numerical value (i.e., the gray tone) of each pixel stands for the evolution at this point. The watershed transform computes the catchments basins and ridgelines, with catchment basins corresponding to image regions and ridgelines relating to region boundaries. The main problem of this algorithm is over segmentation, because all of edge and noise would appear in the image gradient, which make the denoising process necessary. (Vincent, Soille, 1991)(See fig 1).

Fig 1: a) Original Image. b) Image Segmentation by Watershed Transform without any Processing

3. PROPOSED METHOD

Before the segmentation algorithm is performed on the acquired images, we present a method for segmentation utilizing watershed algorithm based on morphological opening-closing filtering and webber perception principle is performed in order to reduce the segmentation drawbacks. The steps of the proposed system are shown in Fig 2.

The first stage removing the noise in the original image by morphological opening/closing reconstruction, then computing the morphological gradient of the denoised image, and the nonlinear transformation for gray level of gradient image is then fulfilled based on Webber perception principle, last the watershed transformation is computed on the nonlinear partitioned gradient image.

3.1. Morphological Reconstruction

Morphological Reconstruction [6], which is developed in recent years, is a nonlinear filter based on mathematical morphology. It makes use of dilation and erosions, which are basic operations in Mathematical morphology. Comparing to other types of filters, morphological reconstruction can keep the information of object contours when filtering the image.

Let the original image is f (x, y), f is called marker, g (x, y) is the mask, f and g are of same size and B is the structuring element, The Morphological Opening Reconstruction is here

The Morphological Closing Reconstruction is

And is the morphological closing for f by B.

The processing of reconstruction can restore those object edges that not be totally eliminated by the opening/closing operation in the image, then the reconstruction opening/closing can remove the peak/ valley that totally contained by the structuring element.

Let the original image is f (x, y), if we make a morphological opening reconstruction on it, then follow
a closing reconstruction, that is

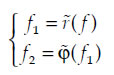
Then in image f2, the fine texture and noise contained in the original image are greatly suppressed, and the main contours of objects are restored by the procedures of reconstruction. The original image is simplified and the information of main contours is kept at the same time.

3.2. Morphological Gradient Calculation

Morphological Gradient highlights sharp gray - level transitions in the input image. After the processing of opening/closing reconstruction, the gradient image is obtained by morphological gradient calculation:

3.3.Nonlinear Transformation of Gray level Based on
Webber Perception Principle

Here we propose a new algorithm based on the Webber perception principle. The Webber perception principle, means difference of gray level W (I) that can be discriminated by human eye is a nonlinear function of the gray level I, the simplest Webber perception function is

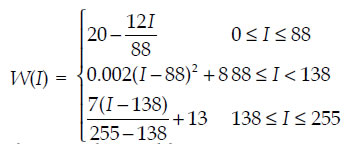
According to the Webber perception principle, Human eye can hardly discriminate the differences of gray levels between, then we can regard the gray levels between as
the same gray level.

By the Webber perception principle which satisfy vision characteristics of human eye, the algorithm of nonlinear transformation of gray level for gradient image is:

1. Set the iteration number n = 1, the beginning gray level I (n) = 0.
2. Calculate the value of W(I(n)) corresponding to I(n) by Webber perception principle.
3. In the morphological gradient image G (f2), set the gray level of all points whose gray level is between [I (n), I (n) + W (I (n))] to I (n) + W (I (n)).
4. Search the points whose gray level is higher than I(n) + W (I(n)) in G (h). If these points does not exist, the iteration ends, or find the lowest gray level Imin in these points, increase the iteration number n = n + 1, and set I(n) = Imin, then turn to step 2.

3.4. Watershed Transformation

By the nonlinear transformation based on Webber perception principle, the gray levels of gradient image G (f2) are incorporated into several rank orders, the gradient image is simplified and main contours of objects in image are kept. The method of watershed transformation is then applied based on the immersion process analogy [9], in which the flooding of the water in the image is efficiently simulated using a queue of pixels. This method will overcome the drawbacks of classical watershed segmentation algorithm.

4. CONCLUSION

In order to solve the over-segmentation of the traditional watershed, an improved algorithm is proposed which makes use of opening closing filter in morphological reconstruction, and the morphological gradient is calculated, then the gradient image is nonlinear transformed based on the Webber perception principle, last the watershed transformation is fulfilled.

REFERENCES

[1] Malik ,Khan ,”Modified Watershed Algorithm for Segmentation of 2D Images”, Journal of Information science & Information Technology, 6 : No.3, pp. 546-552. 2009.
[2] Hamarneh, G., & Li, X. (2009). Watershed Segmentation using Prior Shape and Appearance Knowledge. Image and Vision Computing, 27(1-2), 59-68.
[3] R.M. Haralick and L. G. Shapiro, Survey: Image Segmentation Techniques, Comput. Vis. Graph. Im.Proc. 29 (1985) 100-132.
[4] K. Haris, S. Efstratiadis, “Hybrid Image Segmentation using Watersheds and Fast Region Merging”, [J]. IEEE Transaction on Image Processing, 7, No. 12, pp.1684-l699, 1998 on, National Central University, Computer Science and Information Engineering.
[5] Cui Ming, Sun Shouqian, Pan Yunhe, “An Image Region Merging Algorithm Based on Modified Fast Watershed Transform” Journal of Computer Aided Design & Computer Graphics, 17 : No.3, pp. 546-552. 2005.
[6] L. Vincent;”Morphological Gray Scale Reconstruction in Image Analysis : Applications and Efficient Algorithms”, [J] IEEE Transactions on Image Processing, 2, No.2, pp.176-
201, 1993.
[7] H.T. Nguyen, M. Worning, etc, “Watersnakes: Energydriven Watershed Segmentation”, IEEE Trans. on Pattern Analysis and Machine Intelligence, 25, No.3,pp.330-342, 2003.
[8] M. Susanta, C. Bhabatosh,. “MultiScale Morphological Segmentation of Gray-Scale Images”, IEEE Trans. on Image Processing, 12, No.5, pp.533-549, 2004.
[9] Vincent, P. Soille, “Watersheds in Digital Space: An Efficient Algorithms based on Immersion Simulation”, [J]-IEEE Transactions on Pattern Analysis and Machine Intelligence, 13, No.6, pp.583-598, 1991.