Упрощенный алгоритм водораздела

Аннотация

Алгоритм водораздела является основным инструментом математической морфологии для сегментации изображений. Тем не менее, полученное изображение часто получается чрезмерно сегментированным на большое число маленьких областей (бассейнов), большинство из которых не являются значимыми при решении проблемы. В этой статье предложен метод, который использует фильтры открытия/закрытия в морфологической реконструкции и в принципе Вебера.
Ключевые слова: математическая морфология, метод водораздела.

Введение

Сегментация изображения может быть определена, как разбиение его на различные области, каждый из которых обладает определенными свойствами. Однородность таких критериев, как однотонность распределения уровня серого, как правило, используется для группировки пикселей в области.[3] Тем не менее, число полученных областей может быть слишком велико, и большинство из них, вероятно, незначимы, так что необходимо уменьшить общее количество областей.

Водораздел – это разработанный в последние годы алгоритм сегментации изображений, основанный на математической морфологии[1] и привлекший большое внимание из-за быстроты вычислений и высокой точности обнаружения слабых границ соседних областей. Однако классический алгоритм водораздела чувствителен к шумам и может приводить к серьезной чрезмерной сегментации. В этой статье мы предлагаем сегментацию в рамках математической морфологии фильтров открытия/закрытия и принципа Вебера[9] и обсуждаем способ для снижения чрезмерной сегментации.

Применение этого метода сегментации изображений эффективно преодолевает проблему чрезмерной сегментации и дает удовлетворительные результаты. Верный результат сегментирования очень полезен для анализа изображений, прогнозирования и диагностики.

Алгоритм водораздела

Метод водораздела, также называемый преобразованием водораздела – это основанный на областях метод математической морфологии. В географии, водораздел – это хребет, который делит области различных речных систем. Рассматривая изображения, как геологический ландшафт, можно сказать, что линии водораздела - это границы, разделяющие участки изображений. В топографическом представлении изображения I, численные значения (например, уровни серого) каждого пикселя выступают в качестве высоты этой точки. Преобразование водораздела вычисляет водосборные бассейны и линии хребтов, при том что водосборные бассейны - соответствующие области изображения, а линии хребтов – это границы этих областей. Основной проблемой данного алгоритма является чрезмерная сегментация, поскольку все границы и шумы отображаются в градиенте, что делает необходимым процесс удаления шума. (Винсент, Соли, 1991) (См. рис.1)

Рисунок 1. a)исходное изображение b)сегментированное изображение без предварительной обработки

Первый этап удаления шума в начальном изображении состоит в применении морфологических операций закрытия/раскрытия, затем вычисляется морфологический градиент изображения без шума и выполняется нелинейное преобразование для уровней серого на градиенте изображения при помощи принципа Вебера, последний этап – вычисление водораздела по нелинейному, разбитому на области, градиентному изображению.

Морфологическая реконструкция

Морфологическая реконструкция[6], разработанная в последние годы, является нелинейным фильтром, основанным на математической морфологии. Она использует функции расширения и эрозии, которые являются простейшими операциями математической морфологии. По сравнению с другими типами фильтров, морфологическая реконструкция может сохранить информацию о контурах объекта при выполнении фильтрации.

Пусть исходное изображение (x, y), F называется маркером, g(x, y) – это маска, f и g имеют одинаковую размерность, B – это элемент структурирования. Морфологическое раскрытие:

Где - это морфологическое раскрытие для f по B.
Морфологическое закрытие:

И - это морфологическое закрытие для f по B.

Обработка реконструкцией может восстановить те границы объектов, которые не были полностью удалены с помощью операций раскрытия/закрытия, а затем реконструкцией раскрытия/закрытия возможно удалить пики, которые полностью содержатся в структурированном элементе. Пусть исходное изображение f(x,y). Если мы подвергнем его морфологическому раскрытию, а затем закрытию, то получим:

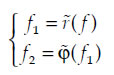
Теперь в изображении f2 хорошая текстура, а шумы, которые содержались в исходном изображении, сильно подавлены, а также с помощью процедур реконструкции будут восстановлены основные контуры объектов. Исходное изображение упрощено, но в то же время, сохранена информация об основных контурах.

Расчет морфологического градиента

Морфологический градиент подчеркивает резкие перепады уровней серого на исходном изображении. После обработки раскрытием/закрытием, с помощью вычисления морфологического градиента будет получен следующий градиент:

Нелинейное преобразование уровней серого, основанное на принципе Вебера

Здесь мы предлагаем новый алгоритм, основанный на принципе Вебера. Принцип Вебера подразумевает, что различия уровней серого W(I), которые могут быть замечены человеческим глазом – это нелинейные функции градаций серого I, простейшей функцией Вебера является:

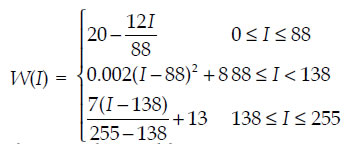
В соответствии с принципом Вебера,  человеческий глаз едва ли различает отличия уровней серого между , поэтому мы можем объединить уровни серого как одинаковые.

По принципу Вебера, которому удовлетворяют характеристики различимые человеческим глазом, алгоритм нелинейного преобразования уровней серого для градиентных изображений будет выглядеть следующим образом:

1. Установить номер итерации n=1, вначале уровень серого I(n) = 0.
2. Вычислить значение W(i(n)), соответствующее I(n) по принципу Вебера.
3. В морфологическом градиентном изображении G(f2) установить уровень серого во всех точках, уровень серого которых лежит в заданных границах.
4. Найти точки, уровень серого которых выше чем заданные. Если таких точек не существует, итерации заканчиваются, либо среди этих точек находятся те, уровень серого которых самый низкий, затем увеличиваем номер итерации, устанвавливаем границу, а затем возвращаемся к шагу 2.

Преобразование водораздела

По нелинейным преобразованиям, основанным на принципе Вебера, уровни серого на градиентном изображении G(f2) объединены в несколько ранговых порядков, таким образом, изображение упрощается и на нем сохраняются основные контуры объектов. Метод водораздела построен на аналогии погружения, при которой моделируется затопление водой очередей пикселей. Этот метод устраняет недостатки, присущие классическому алгоритму сегментации водоразделом.

Заключение

Для того, чтобы решить проблемы чрезмерной сегментации традиционного алгоритма водораздела, предлагается улучшенный метод, который использует фильтры раскрытия/закрытия морфологической реконструкции, а также рассчитывается морфологический градиент, затем этот градиент подвергается нелинейному преобразованию, основанному на принципе Вебера, и в итоге выполняется преобразование водораздела.

Источники

[1] Malik ,Khan ,”Modified Watershed Algorithm for Segmentation of 2D Images”, Journal of Information science & Information Technology, 6 : No.3, pp. 546-552. 2009.
[2] Hamarneh, G., & Li, X. (2009). Watershed Segmentation using Prior Shape and Appearance Knowledge. Image and Vision Computing, 27(1-2), 59-68.
[3] R.M. Haralick and L. G. Shapiro, Survey: Image Segmentation Techniques, Comput. Vis. Graph. Im.Proc. 29 (1985) 100-132.
[4] K. Haris, S. Efstratiadis, “Hybrid Image Segmentation using Watersheds and Fast Region Merging”, [J]. IEEE Transaction on Image Processing, 7, No. 12, pp.1684-l699, 1998 on, National Central University, Computer Science and Information Engineering.
[5] Cui Ming, Sun Shouqian, Pan Yunhe, “An Image Region Merging Algorithm Based on Modified Fast Watershed Transform” Journal of Computer Aided Design & Computer Graphics, 17 : No.3, pp. 546-552. 2005.
[6] L. Vincent;”Morphological Gray Scale Reconstruction in Image Analysis : Applications and Efficient Algorithms”, [J] IEEE Transactions on Image Processing, 2, No.2, pp.176-
201, 1993.
[7] H.T. Nguyen, M. Worning, etc, “Watersnakes: Energydriven Watershed Segmentation”, IEEE Trans. on Pattern Analysis and Machine Intelligence, 25, No.3,pp.330-342, 2003.
[8] M. Susanta, C. Bhabatosh,. “MultiScale Morphological Segmentation of Gray-Scale Images”, IEEE Trans. on Image Processing, 12, No.5, pp.533-549, 2004.
[9] Vincent, P. Soille, “Watersheds in Digital Space: An Efficient Algorithms based on Immersion Simulation”, [J]-IEEE Transactions on Pattern Analysis and Machine Intelligence, 13, No.6, pp.583-598, 1991.