An improved image segmentation approach based on level set and mathematical morphology

ABSTRACT

Level set methods offer a powerful approach for the medical image segmentation since it can handle any of the cavities, concavities, convolution, splitting or merging. However, this method requires specifying initial curves and can only provide good results if these curves are placed near symmetrically with respect to the object boundary. Another well known segmentation technique---morphological watershed transform can segment unique boundaries from an image, but it is very sensitive to small variations of the image magnitude and consequently the number of generated regions is undesirably large and the segmented boundaries is not smooth enough. In this paper, a hybrid 3D medical image segmentation algorithm, which combines the watershed transform and level set techniques, is proposed. This hybrid algorithm resolves the weaknesses of each method. An initial partitioning of the image into primitive regions is produced by applying the watershed transform on the image gradient magnitude, then this segmentation results is treated as the initial localization of the desired contour, and used in the following level set method, which provides closed, smoothed and accurately localized contours or surfaces. Experimental results are also presented and discussed.

Keywords:level set, watershed transform, image segmentation, medical image processing

1. INTRODUCTION

Image segmentation is an essential process for most sub-sequent image analysis tasks. The general segmentation problem involves the partitioning a given image into a number of homogeneous segments, such that the union of any two neighboring segments yields a heterogeneous segment. In computer vision literature, various methods dealing with segmentation and feature extraction are discussed, which can be broadly grouped into histogram based techniques, edge-based techniques, region based techniques, Markov random field based techniques, hybrid methods which combine edge and region methods, and so on1. However, because of the variety and complexity of images, robust and efficient segmentation algorithm on digital images is still a very challenging research topic and fully automatic segmentation procedures are far from satisfying in many realistic situations, especially in the field of 3D medical image processing.

Among the various image segmentation techniques, level set methods offer a powerful approach for the image segmentation since it can handle any of the cavities, concavities, splitting/merging, and convolution. It has been used in well wide fields including the medical image processing2, 3. However, despite of all the advantages which this method can provide, it requires the prior choice of the most important parameters such as the initial location of seed point, the appropriate propagation speed function and the degree of smoothness. The traditional methods only depend on the contrast of the points located near the object boundaries, which cannot be used for the accurately results of complex 3D medical image segmentation.

Another well-known image segmentation technique is morphological watershed transform, which is based on mathematical morphology to divide an image due to discontinuities4. In contrast to classical area based segmentation, the watershed transform is executed on the gradient image. A digital watershed is defined as a small region that can not assigned unique to an influence zones of a local minima in the gradient image. Also these methods were successful in segmenting certain classes of images; due to the image noise and the discrete character of digital image, they require significant interactive user guidance of accurate prior knowledge on the image structure, and easy to be oversegmentation and lack of smoothness.

In this paper, an algorithm belonging to the category of hybrid techniques is proposed, since it results from the integration of morphological watershed transform and level set method, and develops robust and flexible object segmentation on 3D medical image. The gradient magnitude of the smoothed image is input to the watershed detection function, which is used for rough approximation of the desired contour in the image, and guide for the initial location of the seed points used in the following level set method. Experimental results show that this hybrid method can solve the weakness of each method, and provide accurate, smoothed segmentation results of medical image with low time cost. This paper is organized as the following. The section 2.1 is a brief introduction of the level set method. The section 2.2 introduces the morphological watershed method in image segmentation, and then proposes the new hybrid method. The detailed method is presented in section 2.3. In section 3, the experimental result on the real 3D medical image segmentation is shown. The experiments show that this method can obtain the accurate and smooth segmentation results of medical image with low time cost. Finally, conclusions and possible extension of the algorithm are discussed in section 4.

2. WATERSHED TRANSFORMATION

Since its inception5, the level set method has been used to capture rather than track interfaces. Because the method is stable, the equations are not unnecessarily stiff, geometric quantities such as curvature become easy to compute, and three dimensional problems present no difficulties, this technique has been used in a wide collection of problems involving moving interfaces, including the generation of minimal surfaces, singularities and geodesics in moving curves and surfaces, flame propagation, etching, deposition and lithography calculations, crystal growth, and grid generation.

They embed the initial position of the moving interface C0(x) as the zero level set of a higher dimensional function f, the signed distance to C0, and link the evolution of this new function f to the evolution of the interface itself through a time-dependent initial value problem. At each time, the contour C(t) is given by the zero level set of f. This condition states that

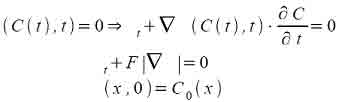
For reasons of causality, it is possible to restrain the computation domain to a band of cells around the zero-level set of f(X; t), for the decrease of the computational cost. Classical approaches are referred to as narrow-band methods. According to the above discussion, the level set method requires specifying initial curves and can only provide good results if these curves are placed near symmetrically with respect to the object boundary. When using the level set method in image segmentation, an initial front should be chose appropriately, and let it propagate with a speed function that stops the motion when the boundary is reached. So the initial front and the speed function are important ones to decide the accuracy of the final segmentation. Thus, level set segmentation is not sufficient for the segmentation of complex medical images; they must be combined with powerful initialization techniques in order to produce successful segmentation. We proposed a rough approximation to the desired contour in the image based on the watershed algorithm. The next section gives a brief introduction about watershed transform.

2.2 The watershed transform

The watershed transform proposed by Vicent and Soille4 is a well known segmentation technique, which is based on immersion simulation, and allows the generation of an initial image partition into regions and consequently, other region-based techniques can be used in order to produce closed, one pixel-wide contours or surfaces. The technique is based on the assumption that image contours correspond to the crest lines of the gradient magnitude image which can be detected via watershed tracing. The principle is briefly described as following: let I be a grayscale digital image, the gradient image ||ÑI|| is computed; for each object of interest, an inside particle is detected (either interactively or automatically); flood waves are propagated from the set of markers and flood the topographic surface ||ÑI||. Watersheds are defined as the lines separating the so-called catchment basins, which belong to different minima. The catchment basin will flow down to the minimum M. When the water reaches the maximum grey value, the edges of the union of all dams form the watershed segmentation. The strength of watershed segmentation is that it produces a unique solution for a particular image, and it can be easily adapted to any kind of digital grid and extended to n-dimensional images and graphs. However, the noise in the image results in over segmentation. Another disadvantage of watershed segmentation, again related to the image noise and the image’s discrete nature, is that the final boundaries of the segmented region are lack of smoothness. So it is not an efficient idea to treat the watershed segmentation as the final segmentation. In this paper, the combination of watershed segmentation and level set method resolves the weaknesses of each method by using the watershed to initialize the actual boundaries which then smooth the results based on level set method. The following sub-section gives the detailed algorithm.

2.3 The combination of watershed and level set

In the initial step, the noise corrupting the image is reduced by noise reduction technique. This noise suppression allows a more accurate calculation of the image gradient and reduction of the number of the detected false edges. Except for the preprocessing stage, our segmentation strategy will consist in using watershed transform as a pre-segmentation tool, and then refine the segmentation result with the level set method. This approach combines the advantages of both methods: the watershed transform pre-segmentation is rough but quick, and the level set needs only a few iterations to produce the final, fast, highly accurate, and smooth segmentation.
The decision of choosing the watershed segmentation as the initialization of the following level set method is according to the following reasons. The first reason is, it is possible that the real boundary of interesting objects is overlapping with the result of watershed transform, it is better for the narrow band decision, the blindness of segmentation is reduced, and the accuracy of segmentation is improved. The second reason is for improving the computation speed. It is no need to computer the arriving time of the inside point of the sub-regions, so the whole computation cost will be reduced.
The watershed algorithm is applied to the gradient magnitude of the original image data set. Among the existing watershed algorithms, a 3D analogy of the immersion-based approach of Vincent and Soille’s watershed algorithm4 was used because of its accuracy and speed of computation. The output of the watershed algorithm is a partitioning of the input data in volume regions of which the interior does not contain any sharp gray value transitions. As we know, the algorithm leads inevitably to an over segmentation of the data because all the crest lines of the data set are detected.
Therefore, the noise filtering preprocessing need to be applied to the image data first.
After the initial segmentation based on watershed transform, the final segmentation is accomplished based on level set method. By combining watershed transform and level sets, this method is able to produce highly accurate segmentations of topologically and geometrically complex structures in much less time than where level sets alone.
The detailed algorithm is the following:
1. Smooth the original image to remove the noise;
2. Compute the gradient value of smoothed image;
3. Choose the appropriate region scale to calculate the local minimum for watershed segmentation;
4. Watershed segmentation;
5. Obtain the interesting boundary;
6. Smooth the boundary using level set method;

3. EXPERIMENTIAL RESULTS AND DISCUSSION

The 2D images shown in the following Fig.1 were used in order to illustrate the stages of the hybrid segmentation algorithm and visually assess the quality of the segmentation results.

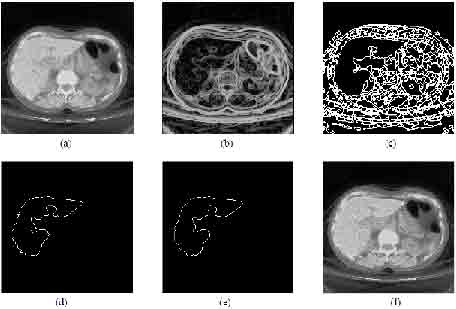
Figure 1: (a) The original slice from a 256 × 256 ×13 liver MRI image; (b) The gradient image; (c) Watershed transform
segmentation;
(d) Frontier image; (e) Smoothed boundary using level set method; (f) the final segmentation result.

4. CONCLUSIONS

In this paper, we have presented a fast hybrid segmentation algorithm which integrates watershed transform and level set method. Both methods have a common advantage: they have no constraints or hypothesis on topology, which may change during convergence. The proposed algorithm allows the interactive control of the stopping point by sorting intermediate partitions. In other words, the user may select the iteration at which the resulting segmentation is acceptable. In the domain of medical image analysis, time-consuming algorithms are synonymous with non-interactive methods, and are therefore limited to a very small number of specific applications. In others words, the computation times of level sets are an obstacle to a wider use of these methods. The combination of the two minimizes user interaction and speeds up the entire segmentation process. This algorithm was implemented for the 2D and 3D cases and produced very satisfactory results both with respect to segmentation performance and execution times. Watershed transform provide a fast and rough initialization, near the solution. Furthermore, it also gives a statistical study of the pre-segmentation (for the level-sets forces): looking at the local distribution of the different regions extracted with the competitive front, we are able to give the initial values of the region descriptors. Further research is directed toward the improvement of the 3D version of the algorithm and its extension to the segmentation of 3D medical image with the consideration of the geometry structure of interesting objects and the statistical characteristics of sub-regions.

REFERENCES

1. K. Haris, et al., “Hybrid Image Segmentation using Watersheds and Fast Region Merging”, IEEE Trans Image Processing, 7(12), 1684-1699, 1998.

2. R. Malladi, J. A. Sethian, B. C. Vemuri, “Shape Modeling with Front Propagation: A Level Set Approach”, IEEE Trans. PAMI, 17, 158-175, 1995.

3. J. A. Sethian, Level Set Methods: Evolving Interfaces in Geometry, Fluid Mechanics, Computer Vision and Material Science, Cambridge University, UK, 1996.

4. L. Vincent, P. Soille, “Watersheds in Digital Spaces: An Efficient Algorithm based on Immersion Simulation”, IEEE Trans. PAMI, 13(6), 583-598, 1991.

5. S. Osher, J. A. Sethian, “Fronts propagating with curvature dependent speed: algorithms based on the Hamilton- Jacobi formulation”, Journal of Computational Physics, 79, 12-49, 1988.

6. A. Elmoataz, S. Schupp, et al., “Using Active Contours and Mathematical Morphology Tools for Quantification of Immunohistochemical Images”, Signal Processing, 71, 215-226, 1998.

7. J. Serra, Image Analysis and Mathematical Morphology, Academic Press, London, 1982.

8. F. Meyer, S. Beucher, “Morphological Segmentation”, Journal of Visual Communication and Image Representation, 1, 21-46, 1990.

9. Thomas Deschamps, “Curve and Shape Extraction with Minimal Path and Level-Sets techniques: Applications to 3D Medical Imaging”, PhD dissertation, MEDISYS of Philips Research Laboratories, Paris/LEP, 2001.