Пирамидальный алгоритм сегментации изображений

1. ВВЕДЕНИЕ

Одним из фундаментальных этапов анализа видеоинформации является сегментация изоб- ражения, означающая разбиение поступающего изображения на множество областей, однород- ных в соответствии с теми или иными критериями, и тем самым ассоциируемых с объектами наблюдаемой сцены или их частями. Результатом сегментации является получение карты об- ластей (сегментов) изображения. Мы рассматриваем задачу текстурно-цветовой сегментации, предполагая при этом, что исходные данные представлены в виде обычного цветного RGB изображения, а однородность областей будет определяться на основе оценок их яркостных, цветовых и текстурных характеристик. Исследованию вопроса сегментации изображений посвящено большое количество работ, тем не менее, процедура сегментации остается одной из фундаментальных проблем анализа по- ступающей видеоинформации. В большинстве случаев алгоритмы сегментации строят либо на использовании базовых свойств изображений, таких как однородность на связных областях и разрывность на их границах [1–3], либо на преобразовании сигнала в пространство при- знаков и классификации в этом пространстве [4]. Среди подходов к построению алгоритмов сегментации можно выделить следующие четыре класса, из которых два первых в основном ориентированы на однокомпонентные (монохромные, черно–белые) изображения, тогда как третий и четвертый классы допускают анализ многокомпонентных данных.

1. Разбиение изображения проведением контуров. Заключается в обнаружении контуров с помощью тех или иных операторов, а также в их прослеживании, связывании, и составле- нии из них границ областей. Известно много различных алгоритмов обнаружения контурных границ. Большинство из них основано на том или ином способе фильтрации, преобразующем изображение в некоторый двумерный массив, значения которого соответствуют вероятности нахождения контура в соответствующей точке. Большинство контурных операторов основаны на вычислении первой производной (операторы Робертса, Собеля [5, 6] и др. [1–3, 7–9]) или второй производной (оператор Лапласа [1–3]). Результаты их применения выглядят неплохо с точки зрения визуальной оценки, однако не удовлетворяют ряду формальных критериев, в частности требованиям непрерывности и минимальной толщины контурных линий. Другой известный подход основан на обнаружении так называемых точек перехода через ноль второй производной (“zero crossing”) [9]. Он обеспечивает выполнение указанных требований, однаков результате возникает много несвязанных между собой пятен, недостаточно хорошо соот- ветствующих реальным контурам. Имеются также некоторые другие методы и алгоритмы [1–3, 7, 10]. Альтернативой алгоритмам фильтрации является прослеживание контуров [5, 8]. Для решения задачи сегментации такой подход имеет ряд преимуществ, среди которых: воз- можность получения карты с непрерывными контурными линиями; прослеживание линии в случае небольших нарушений контурных перепадов (разрывов); проведение контурных линий минимальной толщины. Из недостатков можно отметить: сильная зависимость от шумов на изображении, необходимость предварительного выбора начальных точек прослеживания кон- туров, определенные сложности в точках пересечения или ветвления контуров, необходимость дополнительного анализа и фильтрации полученной карты контуров.

2. Морфологический подход. Из подобных методов наиболее известна сегментация по водо- разделам [13, 14]. Она заключается в интерпретации гладких областей как локальных бассей- нов, а контуров между ними как водоразделов. Такой подход достаточно эффективен в случае монохромных изображений, но слабо применим к цветным и текстурным изображениям. 3. Разбиение изображения на однородные области. Здесь в первую очередь необходимо упо- мянуть пороговые методы, использующие как глобальные, так и адаптивные пороги [1, 11, 12]. Подобные методы просты в реализации и вычислительно эффективны, но не универсальны и применимы лишь в случае монохромного сигнала. Известен ряд методов, основанных на процедуре выращивании областей [15, 16], которая состоит в группировке элементов и мелких областей изображения в более крупные, начиная из так называемых “центров кристаллизации”. Проблемы данного метода — выбор критериев близости и подходящего алгоритма остановки процесса выращивания областей [17]. Альтернативой выращиванию является методы, основан- ные на первичном разбиении изображения на множество малых непересекающихся областей и осуществлении последующего их слияния и разделения [18].

4. Классификация в пространстве признаков. Она заключается в выборе отображения набо- ра входных данных в некоторое многомерное пространство признаков и последующее решение классической задачи кластеризации — разбиении выбранного пространства на классы, базиру- ясь на плотности распределения в нем [4, 19]. Данные методы особенно удобны, когда заранее известно количество классов объектов, содержащихся в изображении. Также как правило, предполагается, что обнаруженные в пространстве признаков кластеры отображают связные области [20]. Классическая процедура сегментации может дать неверные результаты, если отображения различных областей исходного изображения в пространстве признаков заметно перекрываются. Для преодоления данной проблемы предлагается расширение пространства признаков, например, путем добавления значений координат изображения [4]. Возможны два пути улучшения результатов сегментации. Первый состоит в нахождении более чувствительных и соответствующих задаче признаков, а второй — в отыскании иного подхода к разработке алгоритма. В настоящей работе используются оба пути. В части выбора признаков исследуется комбинация яркостно–цветовых и текстурных признаков с построением многокомпонентного пространства и выбором метрики в данном пространстве. Для алгоритма сегментации выбран иерархический подход, основанный на преобразовании изображения в граф первичных кластеров (для этого используется пирамидальный алгоритм) и последующем упрощении карты первичных кластеров.

Проблема текстурного анализа исследуется много лет, и основная трудность заключается в отыскании подходящих характеристик, описывающих текстуру. В анализе текстур имеются три основных подхода: структурный, спектральный и статистический. Структурный подход основан на предварительном выделении примитивов и последующей оценке их размещения, тем самым он лучше подходит для анализа регулярных текстур. Спектральные методы ис- пользуют свойства Фурье-спектра и наиболее подходят для отыскания периодичности в изоб- ражении. Более универсальным и адаптируемым является статистический подход. При этом в качестве статистических характеристик чаще всего используются: матрица смежности, авто- корреляция, разности уровней серого, длины серий по направлениям, локальная частота флук- туаций яркости [23–27]. Иногда используется иерархический подход, позволяющий оценивать характеристики на разных масштабах. После 1980-х годов возник интерес к многоканальному и многомасштабному [28] текстурному анализу, а еще позже — к использованию вейвлетов [29, 30] и Габоровских фильтров [30–33], тесно связанных с пирамидальным представлением изображения [30].

2. СТРУКТУРА АЛГОРИТМА СЕГМЕНТАЦИИ

Задача ставится как текстурно-цветовая сегментация изображения. Исходные данные яв- ляются многокомпонентными; поэтому подход к построению алгоритма сегментации был вы- бран из множества двух последних классов методов: разбиение изображения на однородные области путем анализа сходства в пространстве признаков. Главным критерием при этом яв- ляется расстояние между проекциями элементов в пространство признаков, на основе чего осуществляется объединение соседних элементов, или же проведение границы между ними. Хоть в данном алгоритме сегментации существенно и используется пространство признаков, однако в отличие от классического решения задачи кластеризации анализируется не плот- ность распределения, а оценивается близость точек в этом пространстве. Тем самым одним из важнейших вопросов становится выбор метрики в нем. Рассматриваемый алгоритм содержит два уровня (стадии). На первом изображение разби- вается на множество мелких кластеров с помощью пирамидального алгоритма, а на втором происходит их окончательное слияние. Принципиальная структура алгоритма следующая. Первоначально строится объединенное N–мерное пространство признаков, содержащее пре- образованные цветовые и выделенные текстурные характеристики, и осуществляется переход к так называемому векторному изображению, которое является двумерным массивом N–мерных векторов в этом пространстве. Полученное векторное изображение обрабатывается пирами- дальным алгоритмом, преобразующим его в первичный граф кластеров, в котором каждый элемент изображения оказывается соотнесенным тому или иному кластеру — соответствую- щему узлу графа. Тем самым, каждый узел графа отображает соответствующий кластер, а ребра графа — возможные связи между соседствующими кластерами. Необходимые харак- теристики кластеров и их связей с соседними кластерами объединяются в список кластеров, используемый на второй стадии. Полученный на данной стадии граф кластеров представляет лишь предварительный результат сегментации, поскольку размеры первичных кластеров ока- зываются значительно меньше размеров объектов на изображении, а их число, соответственно, значительно больше числа интересующих объектов.

Полное текстурно–цветовое пространство признаков является объединением двух более простых подпространств — цветовых и текстурных признаков. Подпространство цветовых признаков. В качестве цветовых признаков используются сле- дующие характеристики: яркость, цветность и насыщенность (BHS). Данное пространство цветовых признаков совпадает с обычным RGB цветовым пространством с точностью до ко- ординатного преобразования. Существуют различные способы преобразования значений ко- ординат из пространства RGB в пространство BHS (см., например, [2]); мы воспользовались следующими формулами. Пусть r; g; b — координаты точки в исходном RGB пространстве, и u = min(r; g; b)

Подпространство текстурных признаков. Как показывает анализ литературы, в качестве текстурных характеристик используются самые различные оценки локальной изменчивости изображения. В настоящей работе использован многомасштабный набор оценок изменчивости по множеству направлений, которые вычисляются для каждой точки изображения на осно- ве значений локальной вариации v и локального изменения (осцилляции) градиента g вдоль выбранных направлений. Такой подход близок известному методу разностей яркостей, обсуж- даемому в обзорах [27, 34]. В качестве анализируемой информации используются значения яркости B получаемые согласно уравнению (1). Признаки вычисляются следующим образом.

ПИРАМИДАЛЬНЫЙ АЛГОРИТМ СЕГМЕНТАЦИИ ИЗОБРАЖЕНИЙ

k дает предварительное значение текстурного признака: ~tk = vkgk. Для выравнивания призна- ков высоко- и малоконтрастных текстур используется, как это предлагается в [31], функция гиперболического тангенса. Полученное значение tk считается текстурным признаком по направлению k в соответству- ющей точке (m; n) изображения. Значения tk являются достаточно зашумленными; для повы- шения однородности можно рекомендовать использование фильтрации какого-нибудь вида, например, усреднения по локальному двумерному фрагменту размерами h × h точек. Текстура, как очевидно, является масштабно-зависимой характеристикой. Для различе- ния текстур разной периодичности требуется выделение признаков, соответствующих различ- ным пространственным частотам. Чтобы воспользоваться для этого формулой (4), необходимо взять отсчеты с другим шагом, т.е., при сохранении числа точек равным 2L+1, соответствую- щим образом изменить размер самого отрезка. Так, увеличив в 2n раз размер отрезка, диапазон частот увеличится до в 2n раз более низких частот; влияние высокочастотной составляющей спектра можно подавить с помощью фильтрации (например, путем сглаживания). Другим пу- тем изменения диапазона частот может являться предварительное масштабирование самого изображения в те же 2n раз при сохранении размеров отрезков неизменными; такой подход представляется предпочтительным.

Суммарное число текстурных признаков для каждой точки изображения равно KS. В ре- альности достаточными представляются K = 4 и S = 4, т.е. всего формируется и анали- зируется 16 текстурных признаков. Объединенный набор текстурных и цветовых признаков для точки изображения составляет вектор признаков, а все возможное многообразие таких векторов — пространство признаков.

4. МЕТРИКА В ПРОСТРАНСТВЕ ПРИЗНАКОВ

Одним из важнейших аспектов при решении задачи сегментации изображения как выде- ления однородных областей, является вопрос “похожести” элементов и/или кластеров изоб- ражения, т.е. близости их признаков. Поскольку как элементы, так и кластеры могут быть отображены в одно и то же пространство признаков, то вопрос измерения близости может быть переформулирован как введение метрики в пространстве признаков. Важно заметить, что универсальной метрики не существует, ее нет даже для цветового подпространства. Мет- рика, предлагаемая в настоящей работе, разработана специально для задачи сегментации. Между цветовыми и текстурными признаками имеется существенное различие, поэтому было принято решение использовать две отдельные метрики: чисто цветовую в цветовом подпро- странстве и чисто текстурную в текстурном подпространстве, а затем объединить их в общую текстурно-цветовую метрику. Задача построения цветовой метрики известна достаточно давно, и обычно она решается поиском равноконтрастной цветовой метрики [2, 35, 36]; предлагается много различных метрик в цветовом пространстве, среди них хорошо известные UVW, SW, Lab, и т.д. Мы тестировали некоторые из них и пришли к выводу, что они дают близкие и во многих случаях удовлетворительные результаты. Тем не менее, было принято решение использовать новую метрику, близкую SW, но которая лучше соответствует задаче сегментации и позволяет достичь более точных результатов в темных областях изображения

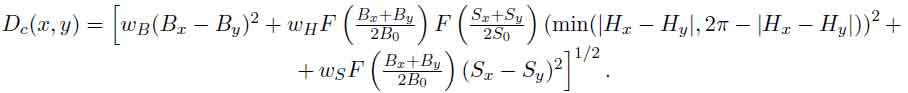
По сути, эта формула ничто иное, как модифицированный вариант корня из суммы квад- ратов разностей значений яркости, цветности и насыщенности двух точек x и y в цветовом подпространстве признаков. Bi, Hi, и Si (i = x; y) суть, соответственно, компоненты ярко- сти, цветности и насыщенности, wB, wH, wS, — весовые коэффициенты, B0 and S0 — пороги подавления, а F(·) — функция подавления, имеющая вид:

Целью введения функции F(·) является подавление излишнего влияния разностей значений цветности и насыщенности в области малых значений яркости, а также значений цветности в области малой насыщенности. Текстурная метрика задается формулой:

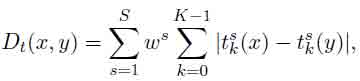
где x и y — две точки текстурного подпространства

5. АЛГОРИТМ ПИРАМИДАЛЬНОГО ПРЕОБРАЗОВАНИЯ (ПЕРВИЧНАЯ СЕГМЕНТАЦИЯ)

Задачей стадии первичной сегментации является преобразование исходного векторного изоб- ражения в первоначальный набор кластеров небольшого размера, в котором каждый сформи- рованный кластер характеризуется как собственными параметрами, так и параметрами связис соседними кластерами. Эта задачу удобно решать с помощью пирамидально–рекурсивного алгоритма [37, 38]. Пирамидальный алгоритм обработки изображения требует задания способа вычисления уменьшенного изображения уровня n + 1 на основе имеющегося изображения уровня n, и применения этой процедуры рекурсивно до предельного уменьшения размера изображения. Часто для этого выбирают элементарный домен некоторой формы, позволяющей плотно по- крыть всю площадь изображения, и задают способ нахождения значения элемента следующего уровня по значениям элементов домена предыдущего уровня. Рекурсивное применение дан- ной процедуры позволяет построить дерево (граф), в котором каждый элемент изображения некоторого уровня (кроме самого нижнего) является узлом, связанным с элементами домена предыдущего уровня, а число нисходящих связей определяется формой и размерами выбран- ного домена. В случае, когда в качестве домена выбран квадрат размерами 2×2 элемента, мы получаем так называемое квадродерево (Рис. 1,а).

Рис. 1. Пирамидальная структура представления данных — квадродерево (а); домен из четырех элементов и его соседние элементы справа и снизу (б).

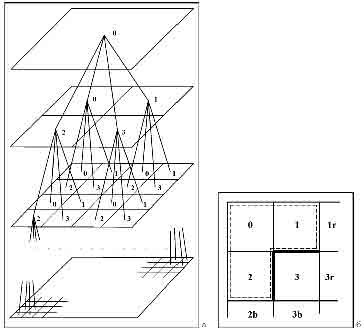
При прямом проходе вверх по квадродереву происходит рекурсивный анализ всех уровней пирамиды, начиная с самого нижнего (исходного изображения) и заканчивая верхним уровнем, состоящим из одного узла; одновременно с этим строится само квадродерево. На каждом шагена основе анализа четырех нижних узлов уровня n создается узел уровня n+1 (см. Рис. 1,а), а в соответствующей структуре нового узла запоминается информация об узлах предыдущего уровня, соединенных с данным узлом, их средней яркости, наличии контуров. Таким образом, каждый узел является вершиной некоторого квадродерева, охватывающего расположенные под ним элементы изображения, и содержит информацию о поддеревьях предыдущего уровня. Основной задачей пирамидального этапа сегментации является объединение соседних эле- ментов, имеющих близкие признаки и не разделенных контуром. Эта процедура требует про- слеживания контурных линий на всех уровнях пирамиды. Считается, что два вертикально или горизонтально соседствующих элемента разделены контуром в том случае, если рассто- яние между их отображениями в пространстве признаков (в смысле задаваемой формулой (10) объединенной текстурно-цветовой метрики) превышает некоторый заданный порог. Для второго и последующих уровней процедура обнаружения контуров также учитывает наличие контура на предыдущем уровне. Анализ и объединение элементов домена размерами 2 × 2 (Рис. 1,б) состоит из следующих шагов.

1. Анализ наличия контурных перепадов между парами соседних элементов: 0-1, 2-3, 0-2 и 1-3. Пары элементов (узлов графа), не разделенные контуром, считаются принадлежащими одному и тому же кластеру. На Рис. 1,б показан контур, проходящий между элементами 1 и 3, а также между элементами 2 и 3. Тем самым, элементы 0, 1, и 2 соответствуют некоторому одному кластеру, а элемент 3 — другому кластеру. 2. Выбор наиболее представительного набора элементов, принадлежащих одному класте- ру нижнего уровня (в данном случае в такой набор входят элементы 0, 1, и 2), и передача усредненной информации соответствующему узлу следующего уровня. Оставшийся элемент (номер 3 на рисунке) считается “подвешенным”, информация о нем наверх не передается и сохраняется только в самом описании текущего узла. 3. Создание карты контуров для следующего уровня. Это осуществляется с помощью ана- лиза внутренних элементов самой четверки, плюс четверки соседних с ней элементов в после- довательной развертке, т.е. справа и снизу; согласно примеру на Рис. 1,б будет проверяться наличие контурных перепадов между элементами 1-1r и 2-2b. После окончания прямого прохода по всему квадродереву, каждый узел любого уровня (кроме корневого узла) будет либо принадлежать поддереву, начинающемуся на одном из верхних уровней, либо сам являться корнем некоторого поддерева. При обратном проходе вниз по квадродереву происходит синтез первичных кластеров. На каждом из уровней вершинам новых поддеревьев (т.е. тем, которые оказались “подвешены” на шаге 2 прямого прохода) присваиваются новые номера кластеров; данные номера распро- страняются вниз на все элементы, связанные с данным поддеревом. Эта процедура рекурсив- но распространяется на все дерево с верхнего уровня (вершины дерева) до нижнего (самого изображения); элементы изображения, получившие при этом одинаковые номера, образуют первичные кластеры (первичные сегменты) обрабатываемого изображения.

Процедура синтеза на каждом из узлов дерева состоит в следующем. 1. Если текущий узел не имеет присвоенного номера, он получает следующий свободный номер кластера. 2. Номер кластера, присвоенный текущему узлу, присваивается всем узлам следующего, более низкого, уровня, связанным с текущим узлом при прямом проходе. Результатом данной процедуры является первичная карта кластеров сегментируемого изоб- ражения. Для дальнейшего анализа формируется граф соседства кластеров (каждому кла- стеру соответствует узел графа) и собирается нужная информация, описывающая свойства каждого кластера (число элементов, объединенных в кластере, длина границы, средний цвет и т.д.). Ребра графа соединяют пары соседствующих кластеров, имеющих общую простран- ственную границу, и отображают характеристики их границы, например, длину общей части. Следует заметить, что одним из преимуществ использования предлагаемого пирамидального подхода к сегментации является тот факт, что он во многих случаях позволяет решить про- блему разделения областей, имеющих границу с разрывами. То, как выглядят изображения после операции пирамидальной (первичной) сегментации, можно видеть на Рис. 2(б)–6(б). Согласно структуре алгоритма сегментации, разбиение образовавшихся кластеров на более мелкие части в дальнейшем невозможно. Следовательно, результаты первой стадии должны удовлетворять двум следующим требованиям (качественному и количественному). Качествен- ное требование состоит в том, что первичный набор кластеров должен быть как можно более детализированным, чтобы обеспечить разделение всех областей изображения, которые долж- ны быть отдельными на финальной карте сегментов. Количественное требование заключается в том, что число кластеров первичного набора не должно быть излишне большим, чтобы предотвратить перегруженность процедуры анализа на второй стадии.

ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ

Алгоритм сегментации был реализован на персональном компьютере, и эксперименты про- водились со многими различными типами реальных изображений без существенных ограниче- ний. Тем самым параметры (значения коэффициентов и порогов) подбирались таким образом, чтобы получить наилучшие результаты “в среднем” по сравнительно большому набору тесто- вых изображений различного вида. Разработанный алгоритм продемонстрировал удовлетворительные результаты на большин- стве из доступных изображений, среди которых: тестовые изображения сцен ограниченной сложности, реальные сцены и портреты, изображения из различных баз данных и библиотек, изображения, составленные из текстур альбома [39], а также целый ряд других изображений. Важно заметить, что поскольку алгоритм ориентирован на анализ изображений в обобщенном текстурно-цветовом пространстве, то его возможности сокращаются, если исходное изображе- ние отображается лишь в его подпространство, что происходит, например, при сегментации черно-белого изображения. Тем не менее, даже в таком случае алгоритм демонстрирует при- емлемое качество (см. Рис. 8(b)). Несколько примеров обработки различных изображений показано на Рис. 2–8. Границы сегментированных областей проведены белыми линиями, а внутренние части сегментов за- полнены средним цветом (за исключением Рис. 8, где границы нанесены поверх исходного изображения). Иерархический пирамидальный подход демонстрирует свою эффективность для сегмен- тации изображений. Он допускает модификации путем использования различных цветовых, текстурных или обобщенных метрик. Следует отметить, что предложенный алгоритм может быть применен не только к обычным цветным RGB изображениям, но также и к любым дру- гим многокомпонентным (например, многозональным) изображениям. Необходимо только мо- дифицировать рассмотренную цветовую метрику (7). Расширение пространства признаков в некоторых случаях также может дать улучшение результатов сегментации.

СПИСОК ЛИТЕРАТУРЫ

1. ГонсалесР. ВудсР. Цифровая обработка изображений. М.: Техносфера, 2005.
2. ПрэттУ. Цифровая обработка изображений. т. 1 и 2. М.: Мир, 1982.
3. Rosenfeld A., Kak A. C. Digital Picture Processing. vol. 1 and 2. New York: Academic Press, 1982.
4. ДудаР., Харт П. Распознавание образов и анализ сцен. М.: Мир, 1976.
5. Робертс Л. Автоматическое восприятие трехмерных объектов. В кн.: Интегральные роботы. т.1.
М.: Мир, 1973, стр. 162–208. 6. Sobel I. E. Camera Models and Machine Perception. Ph.D. thesis. Palo Alto, Calif.: Stanford University, 1970.
7. Prewitt J. M. S. Object Enhancement and Extraction. Picture Processing and Psychopictorics. New York:Academic Press, 1970, pp. 75–150.
8. Фурман Я. А., Кревецкий А. В., Передреев А. К., и др. Введение в контурный анализ и его приложения к обработке изображений и сигналов. М,: Физматлит, 2003.
9. Clark J. J. Authenticating Edges Produced by Zero-Crossing Algorithms. IEEE Trans. Pattern Analysis Machine Intelligence, 1989, vol. 12, no. 8, pp. 830–831.
10. Canny J. A Computational Approach for Edge Detection. IEEE Trans. Pattern Analysis Machine Intelligence,
1986, vol. 8, no. 6, pp. 679–698.
11. SahooP.K., Soltani S.,Wong A.K.C., Chan Y.C. A Survey of Thresholding Techniques. Computer Vision,
Graphics, Image Processing, 1988, vol. 4, pp. 233–260.
12. Jain R., Kasturi R., Schunk B. Computer Vision, McGraw-Hill, New York, 1995.
13. Image Analysis and Mathematical Morphology. vol. 2. Serra J. (ed.). New York, Academic Press, 1988.
14. Special issue on Mathematical Morphology and Nonlinear Image Processing. Pattern Recognition, 2000,vol. 33, no. 6, pp. 875–1117.
15. Fu K.S., Mui J.K. A Survey of Image Segmentation. Pattern Recognition. 1981, vol. 13, no. 1, pp. 3–16.
16. Haralick R.M., Shapiro L.G. Image Segmentation Techniques. Computer Vision, Graphics, Image Processing. 1985, vol. 29, no. 2, pp. 100–132.
17. Haralick R.M. Shapiro L.G. Computer and Robot Vision. vol. 2. Reading, MA, Addison-Wesley, 1993.
18. Shapiro L.G., Stockman G.C. Computer Vision. N.J., Prentice Hall, Upper Saddle River, 2001.
19. Jain A.K., Dubes R.C. Algorithms for Clustering Data. Prentice Hall, 1988.
20. Matas J. Kittler J. Spatial and Feature Space Clustering: Applications in Image Analysis. 6th Int. Conf.
on Computer Analysis and Patterns. Prague, Czech Republic, 1995.
21. Яне Б., Цифровая обработка изображений. М.: Техносфера, 2007.
22. Ohta Y., Kanade T., Sakai T. Color Information for Region Segmentation. Computer Graphics, Image
Processing. 1980, vol. 13, pp. 224–241.
23. Pal N.K., Pal S.K. A Review on Image Segmentation Techniques. Pattern Recognition, 1993, vol. 26, no. 9, pp. 1277–1293.
24. Haralick R.M. Image Texture Survey. Fundamentals in Computer Vision. Cambridge, 1983, pp.145-172.
25. Haralick R.M. Statistical and Structural Approaches to Textures. Proc. IEEE. 1979, vol. 67, no. 5, pp. 786–804.
26. Bovik A.C., Clark M., Geisler W.S. Multichannel Texture Analysis Using Localized Spatial Filters. IEEE Trans. PAMI. 1990, vol. 12, no. 1, pp. 55–73.
27. Van Gool L., DewaeleP., Oosterlinck A. Texture Analysis Anno 1983. Computer Vision, Graphics, Image Processing. 1985, vol. 29, pp. 336–357.
28. Roan S.J., Aggarwal J.K. Multiple Resolution Imagery and Texture Analysis. Pattern Recognition. 1987, vol. 20, no. 1, pp. 17–31.
29. Chang T., Kuo C.J. Texture Alalysis and Classification with Three-Structured Wavelet Transform. IEEE Trans. Image Processing. 1993, vol. 2, no. 4, pp. 429–441.
30. Pichler O., Teuner A., Hosticka B.J. A Comparison Of Texture Feature Extraction Using Adaptive Gabor Filtering Pyramidal And Tree Structured Wavelet Transforms. Pattern Recognition. 1996, vol. 29, pp. 733–742.
31. Jain A.K., Farrokhnia F., Unsupervised Texture Segmentation Using Gabor Filters. Pattern Recognition. 1991, vol. 24, no. 12, pp. 1167–1186.
32. Dunn D., Higgins W.E. Optimal Gabor Filters For Texture Segmentation. IEEE Trans. Image Processing. 1995, vol. 4, pp. 947–964.
33. Weldon T.P., Higgins W.E., Dunn D.F., Efficient Gabor Filter Design For Texture Segmentation. Pattern Recognition. 1996, vol. 29, pp. 2005–2015.
34. Carton E.J., Weszka J.S., Rosenfeld A. Some Basic Texture Analysis Techniques. TR-288. Computer vision laboratory, Computer Science Center. Univ. of Maryland, 1974.
35. Jain A.K. Color Distance and Geodesics in Color 3 Space. JOSA. 1972, vol. 62, no. 11, pp. 1287–1291.
36. MacAdam D.L. Projective Transformations of the ICI Color Specifications. JOSA. 1935, vol. 27, no. 9, pp. 294–299.
37. Hunter G.M., Steiglitz K. Operation of Images Using Quad Trees. IEEE Trans., PAMI-1. 1979, no. 2, pp. 145–153.
38. Rosenfeld A., Quadtrees and Pyramids for Pattern Recognition and Image Analysis. Proc. 5th Int. Conference
on Pattern Recognition. Miami Beach, 1980, pp. 802–811. 39. BrodatzP. Textures: A Photographic Album for Artists and Designers. New York, Dover Publications,
1966.