Коды Рида-Соломона
Martyn Riley and Iain Richardson
Перевод с английского: Юрьев И.В.
Источник: http://www.cs.cmu.edu/afs/cs.cmu.edu/project
Введение в коды Рида-Соломона: принципы, архитектура и реализация
1. Введение
Коды Рида-Соломона позволяют исправить ошибки в блоках данных и используются в широком ряде приложений связанных с цифровой коммуникацией и хранением информации. Коды Рида-Соломона используются для исправления ошибок во многих системах, включая:
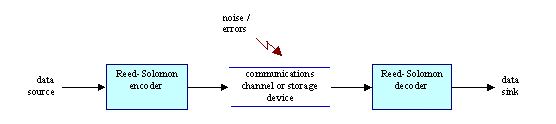
Типичная система показана здесь:

Кодер Рида-Соломона в цифровой блок данных добавляет добавочные "избыточные" биты. Ошибки происходят в течение передачи или хранении информации по ряду причин (например помехи или наложение, царапины на компакт-диске и т.д.) Декодер Рида-Соломона обрабатывает каждый блок данных и пытается исправить ошибки, чтоб вернуть данные в оригинальном виде. Количество и тип ошибок, которые могут быть исправлены, зависит от характеристик кода Рида-Соломона.
2. 2. Свойства кодов Рида-Соломона
Коды Рида-Соломона являются подмножеством кодов БЧХ и являются линейными. Коды Рида-Соломона указываются как RS(n,k) с s-бит символами. Это означает, что кодер берёт k символов данных по s бит каждый и добавляет паритетные символы, чтобы сделать ключевое слово длиной n. Есть также символы с n-k паритетом по s-бит каждый. Декодер Рида-Соломона может исправить вплоть до t символов, которые содержат ошибки в кодовом слове, где 2t = n-k.
Далее показана диаграмма типичного кода Рида-Соломона ( известный как Систематический код, потому что данные слева в неизменном состоянии и паритетные символы присоединены):

Пример:Популярный код Рида-Соломона RS(255,223) с 8-разрядными символами. Каждое ключевое слово содержит 255 байтов кодового слова, из которых 223 байта - данные, и 32 паритетные байты. Для этого кода:
n = 255, k = 223, s = 8
2t = 32, t = 16
Декодер может исправить любые 16 ошибок символа в кодовом слове: т.е. ошибки вплоть до 16 байтов где-нибудь в ключевом слове могут быть автоматически исправлены.
Получим размер символа s, для длины (n) максимального ключевого слова кода Рида-Соломона n = 2s – 1
Например, максимальная длина кода с 8-разрядными символами (s=8) составляет 255 байтов.
Коды Рида-Соломона могут сокращаться (концептуально) бросая ряд нулевых символов данных на кодер, не передавая их, а затем повторно вставляя их в декодер.
Пример: Код описанный выше может быть сокращен до (200,168). Кодер берет блок 168 байтов данных, (концептуально) добавляет 55 нулевых байтов, создает (255,223) ключевое слово и передает только 168 байтов данных и 32 паритетных байта.
Количество "мощность" обработки требует, чтобы кодировались и декодировались коды Рида-Соломона вместе с числом паритетных символов, образуя ключевое слово. Большое значение t означает, что большой ряд ошибок может быть исправлен, но требует большую вычислительную мощность, чем маленькое значение t.
Ошибки Символа
Одна ошибка символа происходит, когда 1 бит в символе неправилен или когда все биты в символе неправильны.
Пример: RS(255,223) может исправить 16 ошибок символа. В наихудшем случае, когда 16 разрядные ошибки, находятся в каждом отдельном символе (байте). В лучшем случае, когда 16 полных байтовых ошибок тогда, декодер исправляет 16 x 8 разрядных ошибок.
Коды Рида-Соломона особенно хорошо исправляют ошибки разрыва (где серии битов в ключевом слове получены с ошибкой).
Декодирование
Алгебраические процедуры декодирования могут исправить ошибки и стирающие сигналы. Стирающий сигнал происходит, когда позиция ошибки символа известна. Декодер может исправить вплоть до t ошибок или вплоть до 2t стирающих сигналов.Информация о стирающих сигналах может часто снабжаться демодулятором в цифровой системе коммуникации, т.е. "флаги" демодулятора получили символы, которые, вероятно, содержат ошибки.
Когда ключевое слово декодировано, есть три возможных результата:
1. Если 2s + r < 2t (s ошибки, r стирающие сигналы) тогда оригинальное передаваемое кодовое слово будет всегда возвращаться,
ИНАЧЕ
2. Декодер обнаружил, что не может вернуть оригинальное кодовое слово и указывает этот факт.
ИЛИ
3. Декодер не исправил возникшие ошибки, то возвращается некорректное кодовое слово без любого указания.
Вероятность каждой из трех возможностей зависит от специфики кода Рида-Соломона, а также от количества и порядка расположения ошибок.
Преимущество кодирования
Преимущество использования кодов Рида-Соломона в том, что вероятность ошибки, остающейся в декодированных данных (обычно), намного ниже, чем вероятность ошибки, если код Рида-Соломона не используется. Это часто рассматривается, как преимущество..
Пример: Проектируется цифровая система коммуникации с вероятностным соотношением ошибки в информации 10-9, то есть не более одной ошибки в109 битов информации. Этого можно достичь повышением мощности сигнала отправки информации или добавляя код Рида-Соломона (или другой тип кода исправляющего ошибки). Код Рида-Соломона позволяет системе достигать исправления ошибок в информации с низшей мощностью сигнала отправителя. Энергетическая "экономия", предоставленная кодом Рида-Соломона (в децибелах), - есть преимущество кодирования.
3.3. Архитектура кодирования и декодирования кодов Рида-Соломона
Кодирование и декодирование кодами Рида-Соломона может осуществляться в программном обеспечении или в специальной аппаратной реализации.
Конечные (Галуа) арифметические поля
Коды Рида-Соломона основаны специальной области математики известной как поля Галуа или конечные поля. Конечное поле использует такие же операции, как и в арифметике (+,-,x,/ и т.д.), которые оказывают влияние на элементы поля и образуют результат. Для кодера и декодера Рида-Соломона необходимо выполнять эти же арифметические операции. Эти операции требуют специального оборудования или программного обеспечения для осуществления функций.
Полиномиальный генератор
Кодовое слово кода Рида-Соломона формируется с помощью специального многочлена. Все допустимые кодовые слова делятся на порождающий полином. Общий вид генератора многочлена:
и кодовое слово построено с помощью:
c(x) = g(x).i(x)
где g(x) является генератором многочлен, i(x) информационный блок, c(x) является действительным кодовым слово и называется примитивным элементом поля.
Пример: Генератор для RS(255,249)
3.1 Архитектура кодера
Паритетные символы 2t в систематическом кодовом слове Рида-Соломона, определяются по формуле:
![]()
Следующая диаграмма показывает архитектуру для систематического RS(255,249) кодера:

Каждый из регистров имеет 6 символов (по 8 бит). Арифметические операции осуществляют ограниченное дополнение поля или умножение на полный символ.
3.2 Архитектура декодера
Общая архитектура для декодирования кодов Рида-Соломона показано на следующей диаграмме.
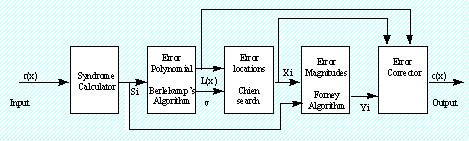
| r(x) | Поступившее кодовое слово |
| Si | Синдром |
| L(x) | Полином локализатора ошибки |
| Xi | Место ошибок |
| Yi | Ошибка в количестве исправляемых ошибок |
| c(x) | Восстановленное кодовое слово |
| v | Число ошибок |
Поступившее кодовое слово r(x) является оригинальным (передаваемым) , кодовое слово c(x) -это оригинальное кодовое слово плюс ошибки:
r(x) = c(x) + e(x)
Поступившее кодовое слово r(x) является оригинальным (передаваемым) , кодовое слово с (х)-это оригинальное кодовое слово плюс ошибки: Декодер Рида-Соломона осуществляет попытку определить место и количество (до t) ошибок (или 2 t стирающих сигналов), а также исправляет ошибки или стирающие сигналы.
Расчёт синдрома
Это аналогичные вычисления паритетности расчёта. Кодовое слово Рида-Соломона имеет 2t синдромов, которые зависят только от ошибки (кодовое слово не передаётся). Синдромы могут быть рассчитаны путём замены 2t порождающего полинома G (х) на корни R (X).
Поиск месторасположения ошибочного символа
Это предполагает решение системы уравнений с t неизвестным. Некоторые алгоритмы могут сделать это быстро. Эти алгоритмы используют специальную матричную структуру кодов Рида-Соломона, что значительно сокращает требуемые вычислительные нагрузки.
Поиск ошибки полиномиальным локатором
Это может быть сделано с помощью алгоритма Берлекэмпа-Мэсси или алгоритма Евклида. Алгоритм Евклида имеет тенденцию быть более широко использующимся на практике, поскольку его легче осуществить: однако, алгоритм Берлекэмпа-Мэсси как правило, приводит к более эффективным аппаратным и программным реализациям.
Поиск корней этого полинома
Для этого используется алгоритм поиска Чин.
Поиск значения ошибки в символе
Опять же, для этого предполагает решение системы уравнений с t неизвестными. Для этого широко используется алгоритм быстрого поиска Форни.
4.Реализации кодера и декодера Рида-Соломона
Аппаратная реализация
Существует ряд коммерческих аппаратных реализаций. Многие существующие системы используют "готовые" встроенные интегральные схемы, кодирования и декодирования кодов Рида-Соломона. Эти микросхемы, склонны к поддержке определенного языка программирования (например, RS (255, k), где t = 1 до 16 символов). Последние тенденция к VHDL или Verilog проектов (логика ядер или ядер интеллектуальной собственности). Они имеют ряд преимуществ по сравнению со стандартной микросхемой. Логика ядра может быть интегрирована с другими VHDL или Verilog компонентами и синтезирована на FPGA (Field Programmable Gate Array) или ASIC (Application Specific Integrated Circuit) - это дает возможность так называемых конструкций "систем на кристалле", в которых несколько модулей могут быть объединены в одной микросхеме. В зависимости от объемов производства, логика ядра часто по стоимости значительно ниже, чем стоимость системы интегральных схем типа "стандарт". С помощью логики ядра, проектировщик избегает потенциальную необходимости "тратить своё время на покупку" интегральной схемы Рида-Соломона.
Программная реализация
До недавнего времени внедрение программного обеспечения в режиме "реального времени" требовало слишком много вычислительных мощностей, за исключением простейших кодов Рида-Соломона (т.е. кодов при малых значениях t). Основная трудность в реализации кодов Рида-Соломона в программном обеспечении то, что общецелевые процессоры не поддерживают арифметических операций поля Галуа. Например, для реализации в программном обеспечении поля Галуа требуется тест на 0, два журнала по таблице окна, сумма по модулю и анти-журнал по таблице. Тем не менее, тщательная разработка вместе с ростом производительности процессоров означает, что внедрённое программное обеспечение может работать при относительно высоких скоростях передачи данных. В следующей таблице приведены некоторые примеры базовых показателей на 166 МГц Pentium PC:
| Код | Скорость передач данных |
| RS(255,251) | 12 Мбит/с |
| RS(255,239) | 2.7 Мбит/с |
| RS(255,223) | 1.1 Мбит/с |
Эти скорости передач данных только для декодирования: кодирование значительно быстрее, так как требует меньшее колличество вычислительных операций.
5. Рекомендованная литература
В этой статье мы сознательно избежали подробного обсуждения теории выполнения кодов Рида-Соломона. Для более детального изучения просмотрите следующие книги:
1.Wicker, "Error Control Systems for Digital Communication and Storage", Prentice-Hall 1995
2. Lin and Costello, "Error Control Coding: Fundamentals and Applications", Prentice-Hall 1983
3. Clark and Cain, "Error Correction Coding for Digital Communications", Plenum 1988
4. Wilson, "Digital Modulation and Coding", Prentice-Hall 1996
6. Об авторах
Эту статью написали Martyn Riley и Iain Richardson.Более конкретную информацию об авторах можно найти здесь.
Copyright © 4i2i Communications Ltd 1996, 1997, 1998