Библиотека

ЦВЕТОРАЗНОСТНАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЦВЕТА В ЗАДАЧАХ СЖАТИЯ ИЗОБРАЖЕНИЙ

Проводится анализ основных моделей представления цвета для использования в задачах сжатия изо- бражений. Обосновывается наличие структурной избыточности при переходе к цветоразностному пред- ставлению изображений. Предлагается применение цветоразностной модели в методах сжатия изобра- жений, основанных на кодирование серий последовательностей повторяющихся элементов.

Ключевые слова: цветовая модель RGB, цветоразностная модель YCrCb, сжатие изображений, цве- товые компоненты, преобразование цветовых моделей, избыточность изображений.

Введение

Постановка проблемы. Одной из особенностей реалистических изображений является наличие в них структурной избыточности в 2-х измерениях. Как правило, соседние точки по горизонтали и по вертикали в изображении близки по цвету. Кроме того, существует подобие между цветовыми плоскостями R, G и B. Поэтому, при создании подходов к сжатию изображений необходимо использовать особенности структуры изображения [1, 2].

Таким образом, в задачах сжатия изображений большую роль играет не только выбор метода компрессии графики, но и выбор оптимальный модели представления цвета.

Целью статьи является обоснование выбора оптимальной модели представления цвета в задачах сжатия изображений.

Изложение основного материала

Целью процесса сжатия есть получение более компактного выходного потока информационных единиц из изначально некомпактного входного потока путем его преобразования.

Любой метод, подход и алгоритм, реализующий сжатие или компрессию данных, предназначен для снижения объема выходного потока информации в битах при помощи ее обратимого или необра- тимого преобразования. Поэтому, по критерию, связанному с характером или форматом данных, все способы сжатия изображений можно разделить на две категории: с уменьшением психовизуальной избыточности (необратимое сжатие) и без потери качества (обратимое сжатие).

Наиболее известный подход к сжатию информации обратимым путем – это кодирование серий последовательностей. Суть методов данного подхода состоит в замене цепочек или серий повторяющихся байтов или их последовательностей на один кодирующий байт и счетчик числа их повторений. Методы кодирования длин серий использует в основном цветовое пространство RGB.

Проведем анализ моделей представления цвета.
Для самосветящихся объектов, таких как дисплеи мониторов ЭВМ, используется аддитивное формирование оттенков. В этом случае требуемый цвет формируется за счет смешивания оттенков трех основных цветов. Для организации такого представления удобно использование аппаратно- ориентированной модели RGB (Red, Green, Blue – красный, зеленый, синий). С учетом того, что дисплеи формируют видимое изображение с использованием красных, зеленых и синих элементов с различным уровнем свечения, использование цветовой модели RGB позволяет обойтись без дополнительной перекодировки при выдачи представления цифрового изображения на экран. Поэтому основной моделью представления цвета в ЭВМ является RGB, в которой цвет представлен значениями интенсивности красной (R), зеленой (G) и синей (B) компоненты (рис. 1).

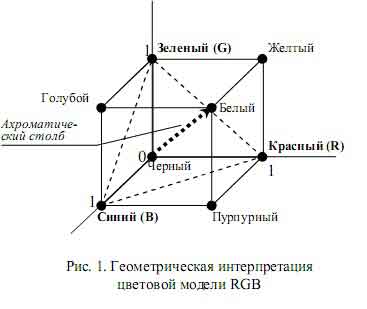
Геометрическая интерпретация представляет собой цветовое тело в виде куба. По осям отсчитываются интенсивности трех основных цветов R, G и B, имеющие нулевое значение в начале координат и единичные значения в максимуме. Вершина куба, расположенная в начале координат (0, 0, 0), соответствует черному цвету. Максимальное значение (1, 1, 1) соответствует белому цвету. Характеристикой каждому цвету служит набор из трех числовых значений, описывающих содержание каждого из основных цветов и ассоциирующийся с пространственными координатами точки, в которой он находится. На диагонали куба, которая соединяет вершины соответствующие черному и белому цвету, располагаются элементы, образованные точками с равными значениями всех трех координат. Такие элементы изображения описываются градациями серого. Диагональ куба это столб ахроматических цветов. Ахроматический столб является осью симметрии данной модели отображения цвета.

Рассмотрим фрагмент изображения с цветовыми компонентами близкими по значению друг к другу. Данные элементы геометрически лежат вблизи ахроматического столба, через который не проходит ни одна из осей координат, поэтому их значения могут быть близки как к 0, так и к 255. Рассмотрим теперь модель представления цвета, у которой через ахроматический столб проходит координатная ось. После перехода к рассматриваемой цветовой модели значения ее двух цветовых координат, соответствующие значениям RGB вблизи серого цвета, будут близки к 0, а значение третьей координаты будет определяться долей каждого цвета в элементе изображения. Тогда на описание этих компонент необходимо меньше затрат машинных разрядов. Поэтому проведем анализ модели представления цвета, в которой через ахроматический столб проходит ось координат, на которой лежат значения яркости изображения.

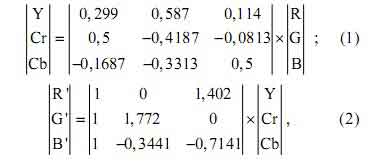
Такая цветовая модель называется цветоразностной моделью представления цвета [3, 4]. В подобной модели элемент изображения описывается яркостью и цветностью, которая получается как взвешенная разность основного цвета и яркости изображения. В этом случае координатная ось яркости будет совпадать с ахроматическим столбом. Одной из распространенных цветоразностных моделей является модель YCrCb, геометрическая интерпретация которой представлена на рис. 2. В данной цветоразностной модели Y – яркостная составляющая, а Сr и Cb – компоненты, отвечающие за цвет (хроматический красный и хроматический синий). В связи с тем, что человеческий глаз наиболее чувствителен к изменению синего цвета, умеренно чувствителен к изменению красного и обладает наименьшей чувствительностью к изменениям зеленого цвета, то основную долю в яркостной компоненте составляет сигнал зеленого цвета, а наименьшую долю – сигнал синего цвета.

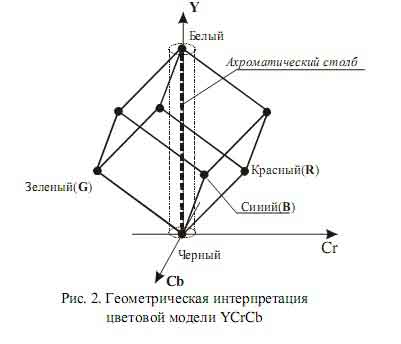
Исходя из этих особенностей, прямое и обратное преобразование между моделями RGB и YCrCb задается соответственно следующими системами выражений [3, 4]:

где R, G, B – матрицы значений цветовых координат элементов изображения в цветовой модели RGB; Y, Cr, Cb – матрицы значений цветовых координат элементов изображения в цветоразностной модели YCrCb; R', G', B' – восстановленные матрицы значений цветовых координат элементов изображения в цветовой модели RGB.

После преобразования выражения (1), переход от цветовой модели RGB к YCrCb примет следующий вид:

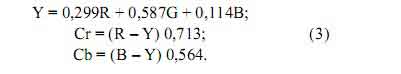
Из формул перевода видно, что сумма коэффициентов при R, G и B в первом уравнения выражения (3) равна 1. Тогда элементу изображения с равными координатами цветовых компонент (R = G = B) после перехода к YCrCb соответствует яркостная составляющая Y, равная цветовым компонентам Y = R = G = B. Из второго и третьего уравнения (2.3) следует, что Cr = Cb = 0. Поэтому, если элемент изображения представлен оттенками серого, то при переводе изображения в YCrCb значения Cr и Cb будут иметь нулевой динамический диапазон, а основную энергию будет нести только яркостная составляющая Y. В общем случае, чем меньше значения R, G, B отличаются между собой, тем ближе к нулю будут значения Cr и Cb после перехода к цветоразностной модели представления цвета. Происходит сокращение динамического диапазона для цветовых компонент Cr и Cb.

Рассмотрим условия, при которых динамический диапазон цветоразностных компонент Cr и Cb будет меньше (больше) динамического диапазона цветовых компонент R и B

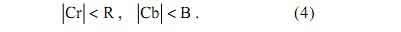
Если значения цветоразностных компонент Cr и Cb положительные Cr >0 ; Cb >0, то для того чтобы динамический диапазон для Cr и Cb был ниже, чем для R и B, необходимо, чтобы:

Если значения цветоразностных компонент Cr и Cb отрицательные Cr < 0 ; Cb < 0, то необходимо, чтобы:

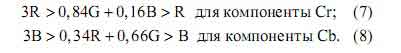
Из анализа геометрических интерпретаций моделей RGB и YCrCb, представленных на рис. 1 и рис. 2 и условий пониженного динамического диапазона для цветоразностной модели представления цвета (5) – (8) вытекают свойства динамического диапазона рассматриваемых цветовых моделей.

Свойства динамического диапазона для модели RGB.

1. Минимальный динамический диапазон для трех компонент R, G и B наблюдается в области черного цвета, так как координаты точек имеют значения близкие или равные 0.
2. Минимальный динамический диапазон для двух цветовых компонент наблюдается по осям координат вокруг точек, описывающих красный, зеленый и синий цвет. Для областей красного, зеленого и синего цвета пониженный динамический диапазон вызван нулевыми или близкими к нулю значениями двух других цветовых компонент.
3. Динамический диапазон для одной компоненты R модели RGB будет ниже динамического диапазона компоненты Cr цветоразностной модели представления цвета, если условия (5) и (7) не выполняются. Динамический диапазон для компоненты B будет ниже динамического диапазона компоненты Cb, если условия (6) и (8) не выполняются.

Свойства динамического диапазона для модели YCrCb.

1. Минимальный динамический диапазон для двух цветоразностных компонент находится вдоль оси яркостной составляющей Y, которая совпадает с ахроматическим столбом. Для области ахроматического столба пониженный динамический диапазон обусловлен нулевыми или близкими к нулю значениями цветоразностных компонент Cr и Cb в случае, когда исходные значения R, G и B незначительно отличаются друг от друга:
   
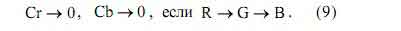
   Из этого свойства, а также из геометрической интерпретации цветоразностной модели представления цвета, представленной на рис. 2 вытекает зависимость цветоразностных компонент от яркости. Так для высокой яркости Y -> 255 или же низкой яркости Y ->0 динамический диапазон Cr и Cb будет минимален.
2. Динамический диапазон для одной компоненты Cr будет ниже динамического диапазона компоненты R при выполнении условий (5) и (7). Динамический диапазон для одной компоненты Cb будет ниже динамического диапазона компоненты B при выполнении условий (6) и (8).

В связи с тем, что крайние значения цветов с нулевыми или близкими к нулю значениями одной или более цветовых компонент наблюдаются реже, чем значения цветов, имеющих ненулевые координаты цветовых компонент, то в модели YCrCb пониженный динамический диапазон цветоразностных компонент Cr и Cb будет наблюдаться чаще, чем для цветовых компонент в модели RGB.

Принимая во внимание то, что наибольшее сжатие изображений достигается при обработке не одного элемента, а вектора, перейдем от рассмотрения скалярной характеристики изображения к векторной. Из анализа выражения (3) видно, что яркостная составляющая несет большую энергетику, а цветовые составляющие Cr и Cb находятся вычитанием из яркостной компоненты Y и умножаются на весовой цветоразностный коэффициент, который меньше единицы. Тогда будут наблюдаться случаи, при которых разность между двумя значениями соседних элементов изображения, после перехода к цветоразностному представлению цвета, будет меньше, чем разность между двумя значениями соседних элементов в модели RGB.

Из выражения (2) разность между цветоразностными компонентами равна:

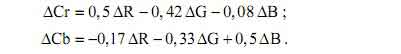
Тогда условия, при которых, разность между двумя значениями соседних элементов изображения, после перехода к цветоразностному представлению цвета, будет меньше разности между двумя значениями соседних элементов в модели RGB:

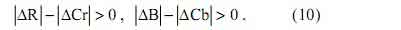
Если изменение цвета на участке изображения, представленного моделью RGB, удовлетворяет условиям минимального диапазона изменения значений между соседними элементами компонент Cr и Cb, то после перехода к YCrCb разница между соседними элементами цветоразностных компонент, исходя из выражения (10), будет близка к 0 и может измеряться десятыми долями. Следовательно, повышается количество элементов, отличающихся друг от друга меньше, чем на 1

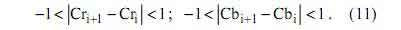
Тогда, если выполняется условие (11), то после приведения значений матрицы YCrCb к целочисленному виду, увеличивается длина последовательности элементов с одной цветовой координатой для матриц Cr и Cb.

Если же значения R, G и B существенно отличаются друг от друга и не удовлетворяют условиям пониженного диапазона изменения значений соседних элементов, то при переходе к YCrCb, исходя из выражения (10), может наблюдаться увеличение разности между значениями соседних элементов цветоразностных компонент ∆Cr и ∆Cb относительно разности между значениями соседних элементов цветовых компонент ∆R и ∆B. Однако, для сильнонасыщенных фрагментов изображения, представленного моделью RGB, длина повторяющичся элементов в основном равна 1. Тогда, даже если и произойдет увеличение разности ∆Cr и ∆Cb между соседними элементами цветовых компонент Cr и Cb, то длина повторяющихся элементов в YCrCb не уменьшится, так как минимальное количество повторяющихся элементов равно 1. Значит, для сильнонасыщенных участков изображения с существенным цветовым перепадом между соседними элементами изменение длины повторяющихся элементов в основном не происходит.

Таким образом, при переходе от RGB к YCrCb происходит увеличение длины повторяющихся элементов для цветоразностных компонент Cr и Cb, в виду того, что разность между значениями соседних элементов в данном случае меньше для цветоразностной модели, чем для модели. Тогда для увеличения степени сжатия при использовании группы методов, основанных на кодировании серий последовательностей, предлагается преобразовывать цветовую модель RGB к YCrCb.

Выводы

В результате проведенного анализа цветоразностной модели представления цвета можно сделать следующие выводы.

Для решения задач сжатия изображений необходимо осуществлять оптимальный выбор модели представления цвета. Так применяя методы сжатия изображений, основанные на кодировании длин серий повторяющихся элементов, предлагается использовать переход от цветовой модели RGB к цветоразностной модели YCrCb. Преимущества модели YCrCb относительно RGB обусловлены пониженным динамическим диапазоном цветоразностных компонент Cr и Cb и наличием структурной избыточности. Тогда в результате перехода к YCrCb происходит увеличение длины повторяющихся элементов для цветоразностных компонент Cr и Cb, вследствие чего увеличивается эффективность работы методов сжатия изображений на основе кодирования длин серий.

Список литературы

1. Методы сжатия данных / В. Ватолин, А. Ра- тушняк, М. Смирнов, В. Юкин. – М.: ДИАЛОГ – МИФИ, 2002. – 384 с.
2. Стрюк А.Ю. Цветовые модели в системах сжа- тия видеоинформации / А.Ю. Стрюк, К.О. Бохан // Радио- электроника и информатика. – 2002. – № 1. – С. 23-25.
3. Гриньов Д.В. Кодирование изображений в цве- торазностном представлении / Д.В. Гриньов // Вісник НТУ „ХПІ”: зб. наук. пр. Тематичний випуск: Інформати- ка і моделювання. – Х.: НТУ „ХПІ”, 2003. – № 26. – С. 107-110.
4. Гриньов Д.В. Математическая модель пред- ставления фотоизображений с использованием цвето- разностных плоскостей / Д.В. Гриньов, О.Д. Анохіна, А.В. Дрімлюга // Системи обробки інформації: зб. наук. пр. – Х.: ХУ ПС, 2007. – Вип. 3 (61). – С. 30-32.