ИССЛЕДОВАНИЯ ПРОЦЕССОВ МЕЖФАЗНОГО ПЕРЕНОСА В ТЕРМОСИФОНЕ

авторы: Полтавский Е. А.

источник:ВСЕУКРАИНСКАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ СТУДЕНТОВ "МЕТАЛЛУРГИЯ ХХI СТОЛЕТИЯ ГЛАЗАМИ МОЛОДЫХ" 2010 год.

          В связи с развитием ряда областей новой техники вопросы передачи тепла от одних устройств к другим приобрели особую остроту. Наиболее ярко это проявилось в ядерной энергетике, электронике, космической технике и в целом ряде научных исследований. Здесь возникло своего рода противоречие между весами и габаритами основных устройств и устройств, отводящих от них тепло. Поскольку теплопроводность твердых тел ограничена, то необходимо искать более эффективные способы передачи тепла. Поэтому возникла необходимость применения испарительно-конденсационных теплопередающих устройств. Одним из таких устройств является термосифон.

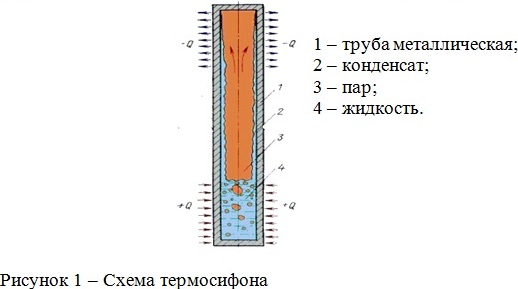
          Тепловая энергия воспринимается от источника и затрачивается на испарение теплоносителя, заключенного внутри корпуса тепловой трубы. Затем она переносится паром в виде скрытой теплоты испарения и далее, на определенном расстоянии от места испарения, в зависимости от тех или иных способов теплосъема, при конденсации пара выделяется в сток. Образовавшийся конденсат возвращается в зону испарения за счет действия массовых сил. При условии, что градиент давления в паре мал, градиенты температур вдоль термосифона также могут быть невелики, что приводит к высоким значениям теплопроводности. Эффективная теплопроводность таких устройств может превышать в 1000 раз теплопроводность медного стержня такого же размера.
          Для вычисления скорости испарения и конденсации внутри термосифона необходимо определить распределение температуры в термосифоне. Для этого воспользуемся уравнением теплопроводности:

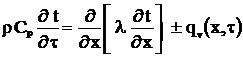
          При дискретизации данного уравнения получаем систему уравнений, которая решается методом монотонной прогонки . Также необходимо учитывать движения теплоносителя внутри трубы. Для описания движения вязкой жидкости принято использовать уравнения Навье - Стокса:

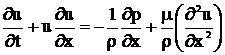
          и уравнение неразрывности течения жидкости:

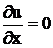
где: u – составляющая скорости движения точки жидкости в направлении оси x, p – давление жидкости, µ– кинематическая вязкость жидкости, p– плотность жидкости. Неизвестными являются величины u, p.
          Вычислив распределение температур по длине термосифона можем вычислить давление в каждом узле разностной сетки по формуле:

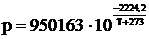
          Аналогично, методом монотонной прогонки вычисляем распределение концентраций. Исходное уравнение:

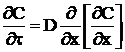
          Для того, чтобы рассчитать поток массы при испарении и конденсации теплоносителя внутри трубы воспользуемся основным уравнением расчета конвективного массообмена:

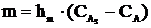
          Используя безразмерные комплексы вычисляем коэффициент конвективного теплообмена при испарении:

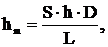
          Коэффициент конвективного теплообмена при конденсации равен:

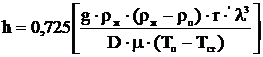
где r`-теплота перегрева пара при конденсации.
          Таким образом, следуя данной методике, можно рассчитать поля распределения концентраций и температур, а также определить поток массы при испарении и конденсации теплоносителя внутри термосифона.