Н.В.Котович, О.А.Славин |
При распознавании печатных и рукопечатных (написанных от руки неслитных образов, сходных с большими печатными буквами) символов могут использоваться хорошо изученные структурные методы, которые предполагают описание образа, разбиваемого на отдельные составные части, описываемые как стабильные идеальные элементы.
В одном из методов [9] было предложено использовать для узнавания топологическое описание изображений, когда последние можно считать плоскими графами, если интересоваться только их внешними и внутренними контурами. При этом в отдельных задачах (автоматическое чтение текста и др.) все возможные изображения, составляющие тот или другой класс, можно представить при отсутствии помех как результат гомеоморфных преобразований некоторого эталонного изображения, соответствующего этому классу. Задача распознавания в этом случае может быть сведена к установлению гомеоморфности предъявленного изображения с одним из эталонных. Ее можно обнаружить с помощью топологических инвариантов — таких свойств изображения, которые не изменяются при его гомеоморфных преобразованиях. Инвариантом, позволяющим дать численное описание изображений, является, например, индекс точки, определяемый количеством сходящихся в ней линий. Соответствующее описание получается обходом в определенном порядке контуров изображения с одновременной фиксацией индексов точек. Установление гомеоморфности — собственно распознавания — сводится к сравнению описаний предъявленного изображения и эталонных изображений классов (см. [9]). Важное достоинство топологического описания — его нечувствительность к сильным деформациям изображения, включающим все преобразования подобия, если связывать с каждым изображением некоторую характерную точку, из которой начинается обход. Обучение топологическому коду состоит в ведении набора эталонных описаний.
Другим структурным методом является описанный в [10] алгоритм событийного распознавания. Событийный метод опирается на топологическую структуру объекта, состоящую из линий и не изменяющуюся при малых деформациях образа. Линией называется часть образа, в каждом сечении которого имеется всего один интервал. Линии, огрубленные на некоторой сетке, определяют события. Событийное представление является не только формальным набором признаков, но и адекватным топологическим описанием. Обучение метода сводится к составлению списка эталонов на достаточно большой последовательности образов. При распознавании для исходного растра определяется событийное представление, которому сопоставляется эталонный класс. Достоинствами метода являются способность к отказам и высочайшее быстродействие. Необходимо отметить устойчивость обучения, заключающуюся в улучшении полноты коллекции при пополнении эталонных наборов.
Недостатками отмеченных структурных методов распознавания является невозможность получения результатов распознавания с оценками сгенерированных гипотез и сильная неустойчивость к ряду деформаций, свойственных отсканированным текстам. Для класса рукопечатных образов разрывы линий являются ожидаемой деформацией. Предлагаемый в настоящей статье алгоритм распознавания, являясь структурным, сочетает в себе такие достоинства как высокое быстродействие и возможность оценки соответствия распознаваемых образов к эталонным описаниям.
Распознавание рукопечатных символов событийным методом обладает рядом недостатков, таких как отсутствие оценок, невозможность распознавания образов, состоящих из нескольких компонент связности, и сильное огрубление представления, часто утрачивающего особые точки, кривизну образа и пр. Рассмотрим набор топологических признаков, процедуру их нахождения и алгоритм распознавания, использующие менее грубое описание буквы, нежели событийный метод.
Распознаваемый символ подвергается процедуре скелетизации (утоньшения). Процедура скелетизации исходных изображений символов, ее использование в системах распознавания текста давно изучается разными авторами, ей посвящена многочисленная литература, см. например [1-7].
Существуют разнообразные методы получения скелетов символов, отличающихся друг от друга. Обзор ряда методов скелетизации дан в [6]. В описываемой системе применялся метод, предложенный Щепиным Е.В. [11]. Этот метод не относится к группе популярных в настоящее время параллельных алгоритмов скелетизации, является последовательным, но его и не предполагалось использовать на машинах с параллельной архитектурой. В то же время данный метод обладает многими преимуществами. Так, этот метод полностью сохраняет 8-и связность исходного изображения, причем для изучения каждой точки (с целью возможного удаления точки с сохранением связности и для выбора направления перехода) в каждый момент требуется знание только окрестности пиксела 3 _ 3. Это позволяет эффективно использовать табличные данные, поэтому алгоритм работает с большим быстродействием — более 1000 символов в секунду на процессоре Intel Celeron 366. Кроме того, этот метод дает скелетное представление толщиной в один пиксел, что исключает необходимость последующей дообработки скелета. Также данный метод позволяет сохранять все особенности исходной картинки, что бывает полезно при анализе тонких случаев распознавания.
Мы использовали следующий алгоритм скелетизации. Вначале происходит разделение исходного образа символа на компоненты связности, для чего может быть использовано линейное представление, сформированное для событийного метода. В каждой компоненте для каждого внешнего и каждого внутреннего контура находятся исходные левые верхние точки. Далее шаг за шагом удаляется один слой точек. Для очередной точки контура рассматривается конфигурация восьми соседних точек. Точка удаляется, если она не является концевой, (то есть не лежит на начальном или концевом интервале прямой или поворотной линии) и если после ее удаления восемь ее соседей будут по-прежнему образовывать связное множество. Отметим, что связность может пониматься по-разному (8-и связность, 4-х связность), поэтому можно легко получать разные виды скелетных представлений. После анализа точки и ее соседей и возможного удаления точки осуществляется переход к следующей точке контура таким образом, чтобы остаться на границе изображения.
За один проход снятие одного слоя точек проводится для каждой компоненты поочередно для каждого внешнего, внутренних контуров. Процедура повторяется до тех пор, пока не останутся только неудаляемые точки. (См. пример на рис.1).
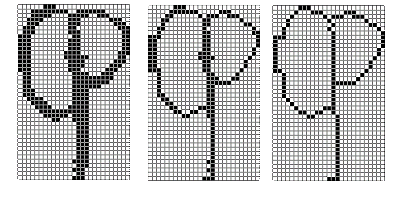
Для ускорения получения скелетного представления применяется ряд технических приемов, таких как получение сведений о возможности удаления точки и о последующей точке перехода по границе с использованием предварительно подготовленных таблиц, а не с помощью вычисления нужных величин.
Получение скелетного представления символа — не самоцель, это изображение используется затем для выделения характеристик символа. Главная задача скелетного представления символа — предоставить возможность для получения ряда характеристик исходного изображения.
Скелетизация играет важную роль во многих системах оптического распознавания. В работе [6] исследованы 10 алгоритмов скелетизации на больших тестовых наборах данных и сопоставлены результаты работы различных алгоритмов утоньшения образов. При этом был сделан вывод, что для распознавания важен не столько алгоритм скелетизации (при совершенно разных алгоритмах сами скелеты все равно достаточно сходны), как последующее использование скелетного представления. При использовании для распознавания одних и тех же признаков для разных скелетных представлений получаются сходные результаты распознавания.
Далее рассмотрим применение скелетного представления для распознавания. Полученное утоньшенное изображение анализируется, фиксируются его следующие параметры: особые точки, структура контура, цепной код.
Особые точки — это концевые точки и точки ветвления (триоды) то есть точки, соседи которых образуют не менее трех связных областей. В примере рис. образ обладает двумя внутренними контурами, одной концевой точкой и тремя триодами. Каждый полученный контур описывается в виде последовательного набора особых точек и, так называемого, цепного кода, состоящим из точки привязки, числа кодов, и массива направлений из очередной точки на следующую точку.
В полученном описании производится огрубляющая предобработка, состоящая в удалении коротких линий, объединении близких триодов, уничтожении малых внутренних контуров.
Для внешнего контура находится его тип или топологический код. Для этого контур записывается в виде последовательного набора номеров особых точек, соответствующих обходу по часовой стрелке. Затем с помощью перенумерации особых точек и изменения начала контура, делается попытка отождествления контура с одним из основных типов, описание которых сгруппированы в таблице 1. Статистический анализ на обучающей последовательности, состоящей из рукопечатных образов заглавных русских букв от «А» до «Я» и цифр от «0» до «9», показал, что контуров, имеющих типы отличные от таблице 1, в сумме составляли меньше 1% всех образов.
Конечно, при изучении иных возможных наборов символов (строчные буквы, буквы иных алфавитов) могут потребоваться другие топологические коды, поэтому была разработана специальная процедура получения набора типичных топологических кодов для заданного множества. Несложно построить и использовать процедуру распознавания символов по их скелетному представлению без ограничения числа допустимых топологических кодов, что делает ненужным предварительный анализ возможных кодов. Но надо отметить, что использование ограниченного набора топологических кодов имеет и ряд преимуществ, т.к. позволяет для различных кодов легко использовать те или иные специализированные процедуры, выделять для некоторых кодов иные (дополнительные) типы особых точек, например экстремальные точки цепного представления.
Тип (топологический код) |
Код символа, примечание |
0,0,0,0,0,0,0,0,0,0,0,0,0,0 |
O |
1,0,0,0,0,0,0,0,0,0,0,0,0,0 |
В |
1,2,0,0,0,0,0,0,0,0,0,0,0,0 |
Г,Л,П,С ... |
1,2,2,0,0,0,0,0,0,0,0,0,0,0 |
Б,Р,Ь |
1,2,3,2,0,0,0,0,0,0,0,0,0,0 |
Ф - без одной палки |
1,2,2,3,2,0,0,0,0,0,0,0,0,0 |
Я |
1,2,3,2,4,2,0,0,0,0,0,0,0,0 |
Е,Т,У,Ц,Ч,Ш ... |
1,2,3,3,2,4,2,0,0,0,0,0,0,0 |
Ю |
1,2,3,2,4,2,5,2,0,0,0,0,0,0 |
К,Х |
1,2,3,4,3,5,6,5,2,0,0,0,0,0 |
А с хвостом сверху |
1,2,3,2,4,5,4,6,4,2,0,0,0,0 |
И,М,Н |
1,2,3,4,3,5,6,5,7,5,2,0,0,0 |
А с хвостом и крестиком |
1,2,3,2,4,2,5,2,6,2,7,2,0,0 |
Ж |
1,2,3,2,4,5,4,6,7,6,8,6,2,0 |
А с крестиками и верхом |
1,2,3,2,4,5,6,5,7,5,4,8,4,2 |
М |
1,2,2,3,3,2,0,0,0,0,0,0,0,0 |
2 с двумя кругами |
1,1,0,0,0,0,0,0,0,0,0,0,0,0 |
8 |
1,2,2,1,0,0,0,0,0,0,0,0,0,0 |
8 с растянутой серединой |
1,2,3,4,2,0,0,0,0,0,0,0,0,0 |
В с хвостом |
1,2,3,4,3,2,0,0,0,0,0,0,0,0 |
А |
1,2,3,4,3,5,3,2,0,0,0,0,0,0 |
А с крестиком |
1,2,3,2,4,5,4,4,2,0,0,0,0,0 |
7 специальная |
1,2,3,2,4,2,5,2,6,2,0,0,0,0 |
Ж индекса 5 |
1,2,3,2,4,5,4,6,4,7,4,2,0,0 |
Н с крестиком |
1,2,3,2,4,2,5,6,5,7,5,2,8,2 |
Ж 5/3 |
1,2,3,4,3,5,3,6,3,2,7,2,8,2 |
Ж 4/4 |
Кратко опишем признаки, используемые при распознавании по полученному скелетному представлению. Для каждой особой точки скелетного представления вычисляются следующие топологические признаки:
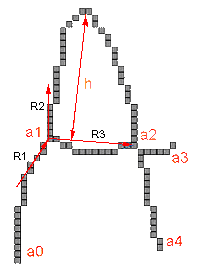
На рисунке 2 условно показаны некоторые из топологических признаков. Граф имеет 4 особые точки — a0, a1, a2, a3. При обходе графа по маршруту a0 ==> a1 ==> a2... в вершине a1 условно показаны следующие признаки: вектор r1 — направление входа в точку, вектор r2 — направление выхода из точки, вектор r3 - глобальное направление на следующую особую точку. Двунаправленный вектор h показывает величину «левого» отклонения дуги (a1,a2) от прямой; «правое» отклонение равно нулю.
Как видно из приведенного описания, число признаков равняется восьмикратному числу вершин. Оно различается для разных топологических кодов, и признаки с одинаковым номером для разных топологических кодов могут иметь разный смысл.
Для некоторых кодов число особых точек и, соответственно, число топологических признаков слишком мало. Так, для кода, соответствующего символу «0», топологических признаков вообще нет, т.к. нет ни одной особой точки. Поэтому могут вычисляться и использоваться следующие дополнительные признаки:
Прогибы вычисляются как расстояния от точек скелетного представления до выпуклой оболочки построенного представления. Дополнительно запоминается положение точек максимального прогиба. Для некоторых топологических кодов число топологических признаков может быть достаточно велико, что может потребовать слишком большого набора эталонов для обучения, поэтому в ряде случаев в распознавании используется часть признаков.
Обучение метода состоит в построении деревьев распознавания для каждого из определенных заранее (вручную или автоматически) топологических кодов. В настоящей версии используется очень простая процедура построения деревьев распознавания, которая приносит, тем не менее, неплохие результаты. Кратко опишем процедуру построения дерева распознавания.
Для каждого топологического кода в обучающем множестве проводится отбор всех имен символов, имеющих
достаточно большое представительство. Для каждого имени проводится анализ имеющихся значений признаков
где N — число признаков для текущего топологического кода. Обозначим Аi — множество имеющихся значений для признака i для символов с именем А. Тогда для каждого i, 0 < i <= N, Аi представляется в виде:
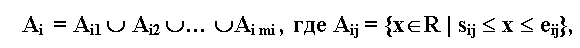
mi различно для каждого i и для каждого A. Далее производится поиск конфликтов. Если для некоторых символов A, B значения признаков пересекаются, т.е.

тогда проводится попытка разрешить конфликт. Делается попытка найти некоторый наилучший для разбиения (наиболее дисперсионный) признак j, выбрать точку деления этого признака k, и разбить множество А на два непересекающихся подмножества A', A'' таким образом, что
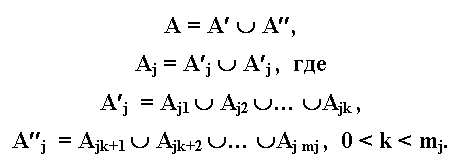
Затем процедура повторяется, т.е. для каждого A', A'' проводится построение областей значений признаков и поиск конфликтов с разноименными символами с возможной дальнейшей разбивкой множеств A', A'' и т.д. Конечно, все конфликты разрешить удается не всегда, поэтому при распознавании в ряде случаев будет выдаваться не одна альтернатива, а несколько. Оценки результирующих альтернатив будут зависеть как от значений признаков (топологических и не топологических), так и от представительности конфликтующих символов в обучающем множестве.
Таким образом, распознавание является древовидным, текущее дерево распознавания выбирается с помощью топологического кода.
Если символ после прохода по дереву распознавания остался нераспознанным, делается попытка улучшения изображения с помощью следующих операций:
Если модификации представления невозможны, то образ остается нераспознанным. Иначе выполняется модификация изображения с возможной повторной скелетизацией — в зависимости от типа модификации. За каждую операцию назначается штраф, который зависит от вида операции и величины модификации (длины добавленной или отброшенной линии, размера «замазываемой» дыры и т.п.).
Среди имеющихся возможностей выбирается набор операций с минимальным штрафом, и процедура распознавания может повторяться несколько раз. Штраф вычитается из фиктивной древовидной оценки 255, назначаемой терминальным символам. Коллекции альтернатив, полученных при различных модификациях, объединяются.
Вопрос, который естественно возникает при модификациях исходного символа — когда пора остановиться с тем, чтобы не получить ложного ответа, и чтобы время распознавания не слишком увеличивалось. В таблице 2 показаны результаты распознавания одной и той же выборке образов рукопечатных символов плохого качества при помощи одного и того же дерева распознавания, но с различным максимальным числом дополнительных итераций. Всего в тестовой последовательности было 53777 символов.
| Число дополнительных итераций |
Точность распознавания (%) |
Полнота распознавания (%) |
Ошибки первой альтернативы (%) |
Отказы (%). | Время (сек). |
| 0 | 80,2 | 80,9 | 1,9 | 17,9 | 47 |
| 1 | 92,5 | 93,4 | 2,8 | 4,7 | 54 |
| 2 | 94,4 | 95,4 | 3,1 | 2,5 | 56 |
| 3 | 94,8 | 95,8 | 3,4 | 1,8 | 58 |
| 4 | 95,0 | 96,0 | 3,5 | 1,5 | 59 |
Как видно из приведенной таблицы, точность и полнота распознавания постоянно увеличиваются с ростом числа итераций, но в то же время после второй итерации рост числа ошибок первой альтернативы почти равен росту верно распознанных символов.
После распознавания ряда конкурирующих букв (таких как «И»—«Н», «А»—«Д», «К»—«Х» и т.п.) может проводиться дополнительный анализ с целью разделения альтернатив, получивших одинаковые оценки.
На тестовой последовательности вычислялся набор характеристик качества, определенный для распознающих алгоритмов в [6]. Определялись такие показатели как точность распознавания (доля правильно распознанных символов по отношению к числу символов в тестовой выборке), полнота коллекции (доля символов тестовой выборки, обладающих альтернативой с правильным кодом), быстродействие (число образов, распознанных в единицу времени), а также способность к отказам и деформациям образов. Характеристики метода распознавания по скелетным признакам на тестовой последовательности рукопечатных символов таковы: точность — 95.6%, полнота коллекции — 96.1%, способность к отказам — 2%, быстродействие — 1000 образов/сек. Высокое быстродействие, обусловленное древовидным распознаванием, может быть увеличено при совместной работе с событийным распознаванием за счет подсчета ряда признаков по линейному представлению. Отметим хорошие характеристики точности и способности к отказам. Также к числу достоинств метода относится устойчивость к деформациям типа разрыв, изгиб линий, малые отверстия в площади образа, появления малых линий, указанные искажения уменьшают оценки распознанных символов. Устойчивость обеспечивается алгоритмом построения представления и дает методу преимущество в распознавании рукопечатных образов, которым свойственны п одобные деформации.
Как видно из приведенного описания, распознавание символов при помощи указанного метода на основе скелетизации можно еще существенно улучшить, в первую очередь за счет изменения, усложнения процедуры обучения и распознавания. Так, например, вместо построения дерева распознавания на базе тех же топологических и дополнительных признаков можно построить нейронную сеть для каждого топологического кода. Но в то же время простота использования, легкость и скорость обучения и распознавания являются очень привлекательными.
Необходимо отметить, что в настоящее время программа распознавания на основе скелетизации не используется в системе сама по себе, а используется в комбинации с иными методами распознавания, основанными на совершенно иных принципах, в первую очередь в комбинации с нейронной сетью, построенной на других признаках символов. Такая комбинация различных методов распознавания рукописных символов приводит к хорошим итоговым результатам распознавания.
1. T.Pavlidis. Algorithms for Graphics and Image Processing. Computer Science Press, Rockville,MD, 1982.
2. L.Lam, S.W. Lee, C.Y. Suen, Thinning Methodologies: A Comprehensive Survey. IEEE Trans. Pattern Analysis and Machine Intelligence, vol.14, pp.869-885, 1992.
3. R.Plamondon, C.Y.Suen, M.Bourdeau, C.Barriere. Methodologies for Evaluating Thinning Algorithms for Character Recognition. Int'l. J. Pattern Recognition and Artificial Intelligence, special issue thinning algorithms, vol 7, no.5, pp.1247-1270, 1993.
4. S.J.Smith, M.O. Bourgoin, K.Sims, H.L. Voorhees. Handwritten character classification using nearest neighbor in large databases. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.22, no. 9, pp.915-919, Sept. 1994.
5. T. Wakahara. Shape machine using LAT and its application to hand-written character recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.16, no. 6, pp.618-629, June 1994.
6. Lam L., Suen C.Y. An Evaluation of Parallel Thinning Algorithms for Character Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 17, № 9, 1995, pp. 914-919
7. R.Plamondon, S.Srinari. On-Line and Off-Line Handwriting Recognition: A Comprehensive Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.22, № 1, January 2000.
8. S.Madahvanath, E.Kleinberg, V.Govindraraju. Holistic Verification of Handwritten Phrases. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.21, № 12, December 1999.
9. Себастиан Г. Процессы принятия решения при распознавании образов. Киев, 1965 г., 151 c.
10. Славин О.А., Корольков Г.В., Болотин П.В. Методы распознавания грубых объектов. В сб. «Развитие безбумажных технологий в организациях», 1999 г., с. 290-311
11. Е. В. Щепин, Г. М. Непомнящий. К топологическому подходу в анализе изображений. Геометрия, топология и приложения (Межвузовский сборник научных трудов). Москва, Мин. высшего и средн. спец. образ. РСФСР, Московский институт приборостроения, 1990 г., с. 13-25.