Социометрия: исследование межличностных отношений в группе.
Источник:
http://psyfactor.org/moreno.htm
Социометрическая техника, разработанная Дж. Морено,
применяется для диагностики межличностных и межгрупповых отношений в целях их
изменения, улучшения и совершенствования. С помощью социометрии можно изучать
типологию социального поведения людей в условиях групповой деятельности, судить
о социально-психологической совместимости членов конкретных групп.
Социометрическая процедура может иметь целью:
а) измерение степени сплоченности-разобщенности в группе;
б) выявление «социометрических позиций», т. е. соотносительного авторитета
членов группы по признакам симпатии-антипатии, где на крайних
полюсах оказываются «лидер» группы и «отвергнутый»;
в) обнаружение внутригрупповых подсистем, сплоченных образований, во главе
которых могут быть свои неформальные лидеры.
Использование социометрии позволяет проводить измерение авторитета
формального и неформального лидеров для перегруппировки людей в командах так,
чтобы снизить напряженность в коллективе, возникающую из-за взаимной неприязни
некоторых членов группы. Социометрическая методика проводится групповым
методом, ее проведение не требует больших временных затрат (до 15 мин.). Она
весьма полезна в прикладных исследованиях, особенно в работах по совершенствованию
отношений в коллективе. Но она не является радикальным способом разрешения
внутригрупповых проблем, причины которых следует искать не в симпатиях и
антипатиях членов группы, а в более глубоких источниках.
Надежность процедуры зависит прежде всего от
правильного отбора критериев социометрии, что диктуется программой исследования
и предварительным знакомством со спецификой группы.
Социометрическая процедура.
Общая схема действий при социометрическом исследовании заключается в
следующем. После постановки задач исследования и выбора объектов измерений
формулируются основные гипотезы и положения, касающиеся возможных критериев
опроса членов групп. Здесь не может быть полной анонимности, иначе социометрия
окажется малоэффективной. Требование экспериментатора раскрыть свои симпатии и
антипатии нередко вызывает внутренние затруднения у опрашиваемых и проявляется
у некоторых людей в нежелании участвовать в опросе. Когда вопросы или критерии
социометрии выбраны, они заносятся на специальную карточку или предлагаются в
устном виде по типу интервью. Каждый член группы обязан
отвечать на них, выбирая тех или иных членов группы в зависимости от большей
или меньшей склонности, предпочтительности их по сравнению с другими, симпатий
или, наоборот, антипатий, доверия или недоверия и т. д.
Членам группы предлагается ответить на вопросы, которые дают возможность
обнаружить их симпатии и антипатии один до одного, к лидерам, членов группы,
которых группа не принимает. Исследователь зачитывает два вопроса: а) и
б) и дает подопытным такую инструкцию: «Напишите на
бумажках под цифрой 1 фамилию члена группы, которого Вы выбрали бы в первую
очередь, под цифрой 2 — кого бы Вы выбрали, если бы не было первого, под цифрой
3 — кого бы Вы выбрали, если бы не было первого и второй». Потом исследователь
зачитывает вопрос о личных отношениях и так же проводит инструктаж.
С целью подтверждения достоверности ответов исследование может проводиться в
группе несколько раз. Для повторного исследования берутся другие вопросы.
Примеры вопросов для изучения деловых отношений
1. а) кого с своих товарищей из группы Вы попросили бы
в случае необходимости предоставить помощь в подготовке к занятиям (в первую,
вторую, третью очередь)?
б) кого из своих товарищей из группы Вы не хотели бы просить в случае
необходимости предоставлять Вам помощь в подготовке к занятиям?
2. а) с кем Вы поехали бы в продолжительную служебную командировку?
б) Кого из членов своей группы Вы не взяли бы в служебную командировку?
3. а) кто из членов группы лучше исполнит функции лидера (старосты, профорга и
т.д.)?
б) кому из членов группы тяжело будет исполнять обязанности лидера?
Примеры вопросов для изученным личных отношений
1. а) К кому в своей группе Вы обратились бы за советом в трудной жизненной
ситуации?
б) с кем из группы Вам не хотелось бы ни о чем советоваться?
2. а) если бы все члены Вашей группы жили в общежитии, с кем из них Вам
хотелось бы поселиться в одной комнате?
б) если бы всю Вашу группу переформировали, кого из ее членов Вы не хотели бы оставить в своей группе?
3. а) кого из группы Вы пригласили бы на день рождения?
б) кого из группы Вы не хотели бы видеть на своем дне рождения?
При этом Социометрическая процедура может проводиться в двух формах. Первый
вариант — непараметрическая процедура. В данном случае испытуемому предлагается
ответить на вопросы социометрической карточки без ограничения числа выборов
испытуемого. Если в группе высчитывается, скажем, 12 человек, то в указанном
случае каждый из опрашиваемых может выбрать 11 человек (кроме самого себя).
Таким образом, теоретически возможное число сделанных каждым членом группы
выборов по направлению к другим членам группы в указанном примере будет равно
(N-1), где N— число членов группы. Точно так же и теоретически возможное число
полученных субъектом выборов в группе будет равно (N-1). Сразу уясним себе, что
указанная величина (N-1) полученных выборов является основной количественной
константой социометрических измерений. При непараметрической процедуре эта
теоретическая константа является одинаковой как для индивидуума, делающего
выборы, так и для любого индивидуума, ставшего объектом выбора. Достоинством
данного варианта процедуры является то, что она позволяет выявить так
называемую эмоциональную экспансивность каждого члена группы, сделать срез
многообразия межличностных связей в групповой структуре. Однако при увеличении
размеров группы до 12-16 человек этих связей становится так много, что без
применения вычислительной техники проанализировать их становится весьма трудно.
Другим недостатком непараметрической процедуры является большая вероятность
получения случайного выбора. Некоторые испытуемые, руководствуясь личным
мотивом, нередко пишут в Опросниках: «выбираю всех».
Ясно, что такой ответ может иметь только два объяснения: либо у испытуемого
действительно сложилась такая обобщенная аморфная и недифференцированная
система отношений с окружающими (что маловероятно), либо испытуемый заведомо
дает ложный ответ, прикрываясь формальной лояльностью к окружающим и к
экспериментатору (что наиболее вероятно).
Анализ подобных случаев заставил некоторых исследователей попытаться изменить
саму процедуру применения Метода и таким образом снизить вероятность случайного
выбора. Так родился второй вариант — параметрическая Процедура с ограничением
числа выборов. Испытуемым предлагают выбирать строго фиксированное число из
всех членов группы. Например, в группе из 25 человек каждому предлагают выбрать
лишь 4 или 5 человек. Величина ограничения числа социометрических выборов
получила название «социометрического ограничения» или «лимита выборов». Многие
исследователи считают, что введение «социометрического ограничения» значительно
превышает надежность социометрических данных и облегчает статистическую
обработку материала. С психологической точки зрения социометрическое
ограничение заставляет испытуемых более внимательно относиться к своим ответам,
выбирать для ответа только тех членов группы, которые действительно
соответствуют предлагаемым ролям партнера, лидера или товарища по совместной деятельности.
Лимит выборов значительно снижает вероятность случайных ответов и позволяет
стандартизировать условия выборов в группах различной численности в одной
выборке, что и делает возможным сопоставление материала по различным группам.
В настоящее время принято считать, что для групп в 22-25
участников минимальная величина «социометрического ограничения» должна
выбираться в пределах 4-5 выборов. Существенное отличие второго варианта
социометрической процедуры состоит в том, что социометрическая константа (N-1)
сохраняется только для системы получаемых выборов (т. е. из группы к
участнику). Для системы отданных выборов (т. е. в группу от участника) она
измеряется новой величиной d (социометрическим
ограничением). Введением этой величины можно стандартизировать внешние условия
выборов в группах разной численности. Для этого необходимо определять величину d по одинаковой для всех групп вероятности случайного
выбора. Формулу определения такой вероятности предложили в свое время Дж. Морено и Е. Дженнингс: P(A)=d/(N-1),
где Р — вероятность случайного события (А)
социометрического выбора; N — число членов группы.
Обычно величина Р(А) выбирается в пределах 0,20-0,30.
Подставляя эти значения в формулу (1) для определения d
с известной величиной N, получаем искомое число «социометрического ограничения»
в выбранной для измерений группе.
Недостатком параметрической процедуры является невозможность раскрыть
многообразие взаимоотношений в группе. Возможно
выявить только наиболее субъективно значимые связи. Социометрическая структура
группы в результате такого подхода будет отражать лишь наиболее типичные,
«избранные» коммуникации. Введение «социометрического ограничения» не позволяет
судить об эмоциональной экспансивности членов группы.
Социометрическая карточка или Социометрическая анкета составляется на
заключительном этапе разработки программы. В ней каждый член
группы Должен указать свое отношение к другим членам группы по выделенным
критериям (например, с точки зрения совместной работы, участия в решении
деловой задачи, проведения досуга, в игре и т. д.) Критерии определяются в
зависимости от программы данного исследования: изучаются ли отношения в
производственной группе, группе досуга, во временной или стабильной группе.
Социометрическая карточка
|
№
|
Тип
|
Критерии
|
Выборы
|
|||
|
1
|
Работа
|
а) Кого бы вы хотели выбрать своим бригадиром? б) Кого бы вы не хотели выбрать своим бригадиром?
|
|
|
|
|
|
2
|
Досуг
|
а) Кого бы вы хотели пригласить на встречу Нового года? б) Кого бы вы не хотели пригласить на встречу Нового года?
|
|
|
|
|
При опросе без ограничения выборов в социометрической карточке после каждого
критерия должна быть выделена графа, размеры которой позволили бы давать
достаточно полные ответы. При опросе с ограничением выборов справа от каждого
критерия на карточке чертится столько вертикальных граф, сколько выборов мы предполагаем разрешить в данной группе. Определение числа
выборов для разных по численности групп, но с заранее заданной величиной Р(А) в пределах 0,14-0,25 можно произвести, пользуясь
специальной таблицей (см. ниже).
Величины ограничения социометрических выборов
|
Число членов групп |
Социометрическое ограничение d |
Вероятность случайного выбора P(A) |
|
5-7 |
1 |
0,20-0,14 |
|
8-11 |
2 |
0,25-0,18 |
|
12-16 |
3 |
0,23-0,19 |
|
17-21 |
4 |
0,22-0,19 |
|
22-26 |
5 |
0,22-0,19 |
|
27-31 |
6 |
0,22-0,19 |
|
31-36 |
7 |
0,21-0,19 |
Обработка результатов
Когда социометрические карточки заполнены и собраны, начинается этап их
математической обработки. Простейшими способами количественной обработки
являются табличный, графический и индексологический.
Социоматрица (таблица).
Вначале следует построить простейшую социоматрицу.
Пример дан в таблице (см. ниже). Результаты выборов
разносятся по матрице с помощью условных обозначений. Таблицы результатов
заполняются в первую очередь, в отдельности по деловым и личным отношениям.
По вертикали записываются за номерами фамилии всех членов группы, которая
изучается; по горизонтали — только их номер. На соответствующих пересечениях
цифрами +1, +2, +3 обозначают тех, кого выбрал каждый испытуемый в первую,
вторую, третью очередь, цифрами -1, -2, -3 — тех, кого подопытный не избирает в
первую, вторую и третью очередь.
Взаимный положительный или отрицательный выбор обводится в таблице (независимо
от очередности выбора). После того, как положительные и отрицательные выборы
будут занесены в таблицу, надо подсчитать по вертикали алгебраическую сумму
всех полученных каждым членом группы выборов (сумма выборов). Потом надо
подсчитать сумму баллов для каждого члена группы, учитывая при этом, что выбор
в первую очередь равняется +3 баллам (-3), во вторую — +2 (-2), в третью —
+1(-1). После этого подсчитывается общая алгебраическая сумма, которая и
определяет статус в группе.
|
№ |
Фамилия |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
Иванов |
|
+1 |
|
|
+2 |
|
|
+3 |
|
-1 |
|
2 |
Петров |
+1 |
|
|
+3 |
+2 |
|
|
|
|
|
|
3 |
Сидоров |
-1 |
+1 |
|
+2 |
+3 |
|
|
|
|
|
|
4 |
Данилова |
|
+2 |
|
|
+1 |
|
|
|
+3 |
|
|
5 |
Александрова |
+2 |
+1 |
|
+3 |
|
|
-3 |
|
|
-2 |
|
6 |
Адаменко |
|
|
|
|
|
|
|
|
|
|
|
7 |
Петренко |
+1 |
|
|
+3 |
|
|
|
|
|
|
|
8 |
Козаченко |
+1 |
|
+3 |
+2 |
|
|
|
|
|
|
|
9 |
Яковлева |
|
+2 |
|
|
+1 |
|
+3 |
|
|
-1 |
|
10 |
Шумская |
|
+2 |
+1 |
|
+3 |
|
|
|
-1 |
|
|
|
Кол-во выборов |
|
|
|
|
|
|
|
|
|
|
|
|
Кол-во баллов |
|
|
|
|
|
|
|
|
|
|
|
|
Общая сумма |
|
|
|
|
|
|
|
|
|
|
Примечание: + положительный выбор; - отрицательный выбор.
Анализ социоматрицы по каждому критерию дает
достаточно наглядную картину взаимоотношений в группе. Могут быть построены суммарные социоматрицы,
дающие картину выборов по нескольким критериям, а также социоматрицы
по данным межгрупповых выборов. Основное достоинство социоматрицы
— возможность представить выборы в числовом виде, что в свою очередь позволяет проранжировать членов группы по
числу полученных и отданных выборов, установить порядок влияний в группе. На основе социоматрицы строится социограмма — карта социометрических выборов
(социометрическая карта.
Социограмма. Социограмма
— графическое изображение реакции испытуемых друг на друга при ответах на
социометрический критерий. Социограмма позволяет
произвести сравнительный анализ структуры взаимоотношений в группе в
пространстве на некоторой плоскости («щите») с помощью специальных знаков (рис.
ниже). Она даёт наглядное представление о внутригрупповой дифференциации членов
группы за их статусом (популярностью). Пример социограммы
(карты групповой дифференциации), предложенной Я. Коломинским,
см. ниже:

——> позитивный односторонний выбор,
<——> позитивный обоюдный выбор,
------> негативный односторонний выбор,
<------> негативный обоюдный выбор.
Социограммная техника является существенным
дополнением к табличному подходу в анализе социометрического материала, ибо она
дает возможность более глубокого качественного описания и наглядного
представления групповых явлений.
Анализ социограммы заключается в отыскании
центральных, наиболее влиятельных членов, затем взаимных пар и группировок.
Группировки составляются из взаимосвязанных лиц, стремящихся выбирать друг
друга. Наиболее часто в социометрических измерениях встречаются положительные
группировки из 2, 3 членов, реже из 4 и более членов.
Социометрические индексы
Различают персональные социометрические индексы (П.С.И.) и групповые
социометрические индексы (Г.С.И.). Первые характеризуют индивидуальные
социально-психологические свойства личности в роли члена группы. Вторые дают
числовые характеристики целостной социометрической конфигурации выборов в
группе. Они описывают свойства групповых структур общения. Основными П.С.И.
являются: индекс социометрического статуса i-члена; эмоциональной
экспансивности j-члена, объема, интенсивности и концентрации взаимодействия
ij-члена. Символы i и j
обозначают одно и то же лицо, но в разных ролях; i —
выбираемый, j — он же выбирающий, ij
— совмещение ролей.
Индекс социометрического статуса i-члена группы определяется по
формуле:

где Сi — социометрический статус i-члена, R+ и R- — полученные i-членом выборы, Z — знак алгебраического суммирования числа полученных выборов i-члена, N— число членов группы.
Социометрический статус — это свойство личности как элемента социометрической структуры занимать определенную пространственную позицию (локус) в ней, т. е. определенным образом соотноситься с другими элементами. Такое свойство развито у элементов групповой структуры неравномерно и для сравнительных целей может быть измерено числом — индексом социометрического статуса.
Элементы социометрической структуры — это личности, члены группы. Каждый из
них в той или иной мере взаимодействует с каждым, общается, непосредственно
обменивается информацией и т. д. В то же время каждый член группы, являясь
частью целого (группы), своим поведением воздействует на свойства целого.
Реализация этого воздействия протекает через различные социально-психологические
формы взаимовлияния. Субъективную меру этого влияния подчеркивает величина
социометрического статуса. Но личность может влиять на других двояко — либо
положительно, либо отрицательно. Поэтому принято говорить о положительном и
отрицательном статусе. Статус тоже измеряет потенциальную способность человека
к лидерству. Чтобы высчитать социометрический статус, необходимо
воспользоваться данными социоматрицы.
Возможен также расчет С-положительного
и С-отрицательного статуса в группах малой
численности (N).
Индекс эмоциональной экспансивности j-члена группы
высчитывается по формуле

где Ej — эмоциональная экспансивность j-члена, Rj — сделанные /членом выборы
(+, -). С психологической точки зрения показатель экспансивности
характеризует потребность личности в общении.
Из Г.С.И. наиболее важными являются: Индекс эмоциональной экспансивности
группы и индекс психологической взаимности.
Индекс эмоциональной экспансивности группы высчитывается по формуле:
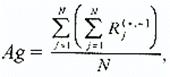
где Ag — экспансивность группы, N — число членов группы? Rj (+,-) — сделанные j-членом выборы. Индекс показывает среднюю активность группы при решении задачи социометрического теста (в расчете на каждого члена группы).
Индекс психологической взаимности («сплоченности группы») в группе высчитывается по формуле:

где Gg — взаимность в группе по результатам положительных выборов, Аij+ — число положительных взаимных связей в группе N — число членов группы.
Литература:
1. Методы психологической диагностики. — М.,
1993
2. Методики социально-психологической диагностики личности и группы.
— М., 1990