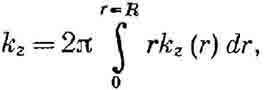
8.3. Методы расчета оседаний, основанные на применении функций распределения
Методы расчета оседаний с применением функций распределения представляют собой своего рода переходную ступень от эмпирических методов к методам, основанным на теоретических моделях массива. Все методы этой группы объединяет то, что в их основе лежат так называемые функции распределения или функции влияния, описывающие характер и степень влияния элементарных площадок, из которых слагается площадь очистной выработки, на земную поверхность. Так, например, изображенный на рис. 100 элемент dA1 очистной выработки вблизи площади полной подработки оказывает на точку Р земной поверхности меньшее влияние, чем находящийся в центре выработки элемент dA2,поскольку он лежит дальше от точки Р и линия, по которой проявляется его влияние, наклонена под меньшим углом к горизонту. Для практического расчета в большинстве методов этой группы бесконечно малые элементы площади палатки объединяются в кольцевые зоны, размеры которых выбираются таким образом, чтобы степень влияния каждой зоны на лежащую в центре палетки точку земной поверхности была приблизительно одинаковой (зоны равного влияния).
При помощи построенной таким способом палатки можно определить ожидаемые оседания в отдельных точках земной поверхности путем простой оценки относительных размеров площадей, покрываемых на плане очистной выработки отдельными зонами палатки, выраженных в долях всей площади каждой зоны. Первый метод расчета оседаний с применением интеграционной сетки был разработан Кейнгорстом еще в 1925 г. [170], но основанные на этом принципе методы расчета движений до сих пор являются в ФРГ наиболее распространенными.
8.3.1. Теоретические основы метода зон равного влияния
Метод интеграционных сеток основан на представлении о граничном угле и об определяемой этим углом площади полной подработки. Эта площадь, имеющая при горизонтальном залегании пласта форму круга, мысленно разбивается на бесконечно малые элементы dA, влияние которых на оседание точки Р земной поверхности, лежащей над центром площади полной подработки, зависит от положения этих элементов относительно упомянутого центра. Опыт показывает, что степень влияния, выражающаяся дифференциальной функцией de/dA = Kz, закономерно убывает с увеличением расстояния r элемента площади dA от центра Р' площади полной подработки. Это распределение влияний отдельных элементов площади полной подработки, характеризующееся свойством круговой симметрии, в различных методах расчета описывается той или функцией распределения Kz, (r), чаще всего в зависимости от величины отношения i = r/R (здесь R — радиус площади полной подработки) или от величины зонального угла в виде Kz (i) или Kz, (q), где tg q = r/Н.
Если на образующих площадь полной подработки элементарных площадках построить вертикальные столбики, высота которых в известном масштабе выражает значения функции распределения для этих площадок, то совокупность этих столбиков образует колоколообразное тело, совпадающее с телом, образуемым вращением кривой функции распределения. построенной для диаметрального сечения площади полной подработки, относительно оси, нормальной к этой площади и проходящей через ее центр [24].
Аналогичным образом можно построить, с учетом масштабного коэффициента Vz «тело элементарных оседаний», состоящее из столбиков, высота которых соответствует оседаниям dVz в точке Р земной поверхности влиянием элементарных площадей dA в соответствии с соотношением KzVz= dVz/dA.
Таким образом, функция распределения Kz, описывает также бесконечно малые изменения dVz величины оседания вблизи точки Р земной поверхности (см. рис. 100), т. е. характеризует наклон dVz,/dx [см. формулы (149) и (262)], вызванный подвиганием на величину dx очистной выработки, имеющей очень малый размер в направлении оси х (dA = dx dy npu dy = 1). Наконец, интеграционная сетка представляет собой проекцию на горизонтальную плоскость областей влияния, выделенных вертикальными цилиндрическими и вертикальными диаметральными сечениями в зонах секторов равного объема (см. рис. 100).
Чтобы иметь возможность вычертить такую интеграционную сетку, нужно, вообще говоря, представить закономерность кольцеобразного прироста объема области влияния от центра к периферии в виде интегральной кривой, описываемой уравнением
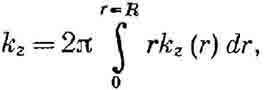
в котором пределами интегрирования предусматривается возможность изменения зоны влияния от нуля до радиуса площади полной подработки. Математическое решение этой задачи для показательной функции распределения можно найти в соответствующей литературе [36, 75]. В то время как в одном из указанных решений объем пропорциональной части области влияния определяется суммированием колец бесконечно малой толщины (2пг dr), шириной dr и высотой Kz, при помощи выражения (151), в другом решении объем части области влияния, разбитой на элементарные цилиндрические объемы горизонтальными сечениями, вычисляется как сумма объемов цилиндрического цоколя (пг2 Kz) и насаженной на него колоколообразной части, состоящей из бесконечно тонких горизонтальных слоев, имеющих высоту dKz и площадь основания пг2. Было предложено еще одно решение [286], в котором площадь, ограниченная осью r и кривой rk2 (r), представляющей собой функцию влияния, умноженную на расстояние r (см. график в нижней части рис. 100), соответствующая объему части области влияния, графически разбивается на пять равновеликих частей.
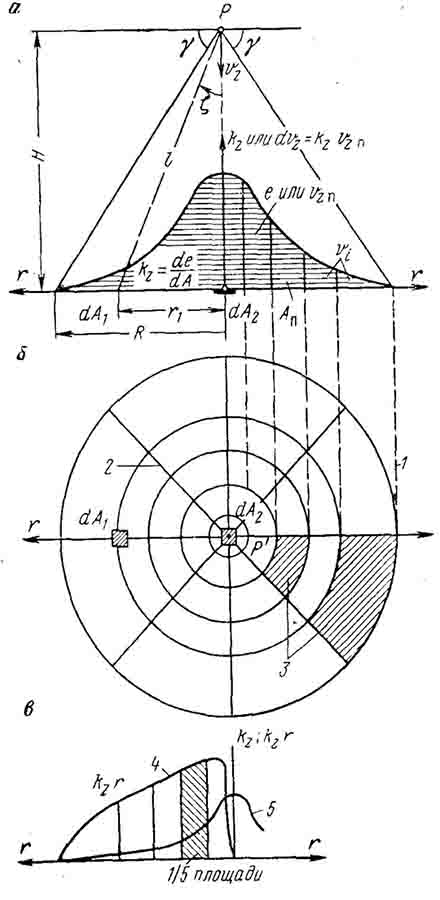
Следовательно, изменение величины Kz, дает по оси ординат конечные значения коэффициентов влияния е кольцевых участков площади очистной выработки на центральную точку Р земной поверхности в зависимости от расстояния r или влияния, обусловленного концентрическим подвиганием очистных работ от точки Р' к внешнему контуру площади полной подработки. Равным образом можно получить из функции распределения интегральную кривую для случая, если площадь полной подработки отрабатывается полосами слева направо (см. методы Бейера и Шпетмана). Если, например, разбить ось ординат (см. рис. 100) на пять равных частей, каждая из которых соответствует Ле = 20%, то выраженные в долях радиуса площади полной подработки зональные радиусы i = rlR могут быть получены из графика как соответствующие значения абсцисс для интеграционной сетки. разбитой на пять зон равного влияния. и перевычислены для данного масштаба плана горных работ. Чтобы облегчить подсчет при практическом использовании интеграционной сетки, ее концентрические кольцевые зоны разбиваются на восемь секторов с одинаковыми центральными углами, равными 45' (см. рис. 100).
Таким образом, отработка большого зонального сектора в краевой части площади полной подработки оказывает на величину оседания земной поверхности в точке Р такое же влияние, как отработка сравнительно небольшого сектора во внутренней части той же площади полной подработки. По их внешнему виду такие интеграционные сетки получили в немецкой терминологии название паутинных сеток. Если имеется интеграционная сетка, построенная для некоторой определенной глубины Н1, то зональные радиусы интеграционной сетки для любой другой глубины Н2, легко могут быть определены графически при помощи чертежа, на котором концы зональных радиусов первой сетки соединяются прямыми линиями («зональными лучами») с точкой Р земной поверхности.