Библиотека по теме магистерской работы

Автор: Dr. Stanislaw Prusek
Перевод с немецкого: магистр ДонНТУ Севрюков Александр.
Источник: http://www.masters.donntu.ru/2007/fgtu/kozir/library/index6.htm.
Статья сокращена. Полную стаью можно посмотреть в журнале "Glückauf" 138(2002) Nr.6 (страницы 269-273 по сборнику журналов за 2002 г.)

При каждом проектировании разработки месторождения полезного ископаемого не избежать многократного использования участковых штреков. На основании этого необходимо поддержать достаточную площадь поперечного сечения штрека за лавой, в зависимости от чего для некоторых целей этот штрек в дальнейшем использовался. Для получения такого поперечного сечения применяют ряд методов и средств, которые главным образом должны противодействовать конвергенции. Эффективный метод это возведение бутовых полос непосредственно за сопряжением с лавой. В качестве материала для заполнения бутовой полосы используют деревянные или бутокостры, но также различные виды строительного сырья (Рис.1).

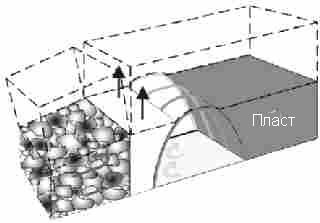
Рис.1 - Бутовая полоса из минерального сырья

Проведенные в прошлом наблюдения и исследования(4,5,6,7,8,9,13) показывают, что влияние материала бутовой полосы на снижение конвергенции штрека за лавой различно. При этом подмечено, что бутовая полоса из минерального сырья еффективнее ограничевает конвергенцию чем из дерева, которая обычно очень податлива. Это состояние воспринимает влияние различных несущих способностей крепи, которые бутовая полоса из минерального сырья или дерева совершенствует. Расчет значения опорной силы для данных подземных условий был до сих пор довольно неточен, и значения были определены не совсем точно.

В последнем году проводилось в польском Горном-Главном Институте исследовательские работы с целью определить влияние различных видов бутовых полос на конвергенцию выемочного штрека. В рамках этих исследовательских работ были определены на основании подземлей проведенных измерений характеристическоя кривой опорной силы бутовой полосы из различных видов минерального сырья, а также и дерева. По окончании была выведена эмпирическая зависимость, которая осуществляет расчет опорной силы для различных видов бутовых полос для определенных горнотехнический и геологических условий.

Метод и область измерений в выемочном штреке

Эмпирическая зависимость, которая осуществляет расчет опорной силы для бутовой полосы, была выведена из результатов измерений по 9-ти выемочным штрекам. В этих выемочных штреках проводили измерения конвергенции, а также опорной силы бутовой полосы, после единственного прохода лавы. При этом установили в этом штреке приблизительно 75 метров перед лавой мест измерения смещений, которые по меньшей мере охватуют 3 измирительных пункта от Р₁ до Р₂ (Рис.2).

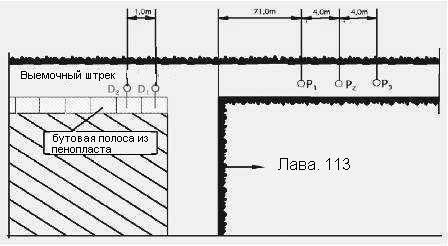
Рис.2 - Порядок пунктов измерения за и перед фронтом очистных работ

В качестве измерительного пункта используется в основном отрезок породного анкера, который были установлены в почве и кровле. Точки замера были упорядочены вдоль оси штрека, при этом станция в кровле упорядочевалась максимально вертикально над соответсвующим пунктом в почве (Рис. 3).

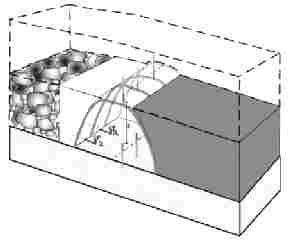
Рис.3 - Порядок мест измерения в выемочном штреке

Измерение конвергенции основывается на получении взаимных смещений измерительных пунктов при приближении или отдалении фронта работ от места измерения. Результаты измерений конвергенции из исследуемого штрека представлены на рис.4.

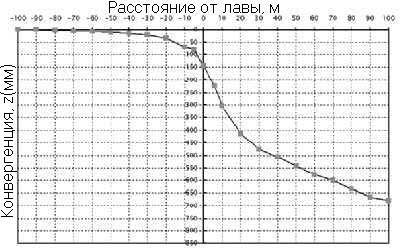
Рис.4 - Пример конвергенции выемочного штрека за и перед фронтом очистных работ.

Для измерения опорной силы бутовой полосы используется специальный динамометр, который был установлен непосредственно за лавой под бутовой полосой (Рис.3) и через высоконанапорный трубопровод был связан с манометром со шкалой показаний давления.Эти динамометры проверены прежде на гидравлическом прессе, смогли определить записанные значения измерения давления в еденицах силы.

Измерение конверегнции, а также считывание показания манометра проводится все 24 часа одновременно с измерением расстояния фронта очистных работ от измерительного пункта.

Определение эмпирической зависимости для расчета опорной реакции

При выведении формулы для расчета опорной силы бутовой полосы предполагается на основании ранее полученных значений исследования Главного-Горного института (1,2,3) а также достигнутых под землёй результатов измерений , что вследствии движения пород каждая бутовая полоса сходится, при чем ее критическое значение конвергенции z_k, для которой опорная силы достигает максимума, может быть установлено.

Это принимается для того, чтобы между конвергенцией бутовой полосы и её достижимой опорной силы установить точную зависимость. Если нарастающее значение ковергенции меньше чем критическое значение z_k , повышается реакция опоры бутовой полосы, а если она больше чем критическая значение z_k, реакция опоры снижается.

Величина конвергенции бутовой полосы z с её критической величиной z_k а также величина реакции опоры были определены для каждой исследуемой бутовой полосы на основании прямых измерений под землёй. Таким образом установлена кривая реакции опоры исследуемых бутовых полос в форме зависимости её реакции опоры от измеренной конвергенции.

Основные ряды измерений протекали в выемочных штреках, в которых бутовые полосы состоят из сырья, такого как Tekblend, Utex и пенопласт. Для того, что бы кривые реакции опоры этих бутовых полос начертить в диаграмме, были нанесены на ось Х координатной системы значения z_рk / z_k , это отношение величины конвергенции к критической величине конвергенции, а на ось Y значения Р_рк / Р_max , это соотношение реакции опоры к максимальной реакции опоры. Так полученное распределение пункта замера показано на рис.5

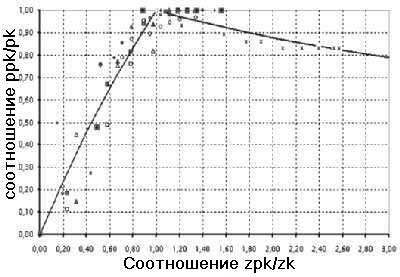
Рис.5 - Кривая реакции опоры бутовой полосы из минерального сырья.

Для пункта представленного на рис.5 вычислены кривые сравнения, характер которых соответствует ближайшему достигнутому распределению пункта, при этом было предположено, что две гиперболические установившиеся кривые принимаются во внимание.

По средствам нелинейного регрессионного анализа, соответствующие преобразования а такжк учет дальнейших факторов, которые определены литературными установками, получить следующую эмпирическую формулу для расчета опорной реакции бутовой полосы:
опорной реакции бутовой полосы из минерального сырья:
максимальной опорной реакции бутовой полосы(МН/м):

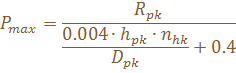
опорной реакции при низких, не превосходящих величин конвергенции критическую величину (МН/м):

опорной реакции при высоких, превосходящих величин конвергенции критическую величину (МН/м):

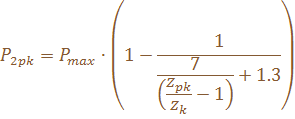
где:

z_рk - конвергенция бутовой полосы (мм);

z_k - критическая конвергенция бутовой полосы (мм);

h_рk - начальная высота бутовой полосы (мм);

D_рk - ширина бутовой полосы (м);

n_рk - фактор ползучести бутовой полосы;

R_рk - прочность на сжатие сырья, из которого бутовая полоса состоит (МПа);

Похоже устанавливается на основании подземных результатов измерений также эмпирическая зависимость для бутовых полос из деревянных костров и бутокостров.

Выводы

Представленная эмпирическая зависимость в существующем вкладе осуществляет расчет реакции опоры бутовой полосы,которую часто используют в угольной промышленности. Эти зависимости могут быть использованы при планировании данной бутовой полосы для выбора соответствующего вида полосы, для выбора параметров минерального сырья, как и для установления её размеров. Бутовая полоса с данными горнотехническими и геологическими соотношениями соответствующей реакции опоры должен суметь обеспечить сохранение достаточного поперечного сечения штрека за фронтом очистных работ.

Список использованной литературы

1. Bilinski, A.: Gebirgsdruckerscheinungen in Kohleflozen n Bruchbauraeumen. In: Wissenschaftliche Hefte der Schlesischen Technischen Hochschule, Nr. 221, 1968.

2. Bilinski, A.: Geomechanische Uberwachung von mechanisierten Streben bei grosser Teufe. Forschungsarbeiten des Hauptinstituts für Bergbau, Nr. 812, 1996.

3. Bilinski, A. ; Kostyk, T.: Einfluss der Stutzkraft des Ausbaus auf die Gebirgsbewegung in Abbaubegleitstrecken beim Bruchbau. Forschungsarbeiten des Hauptinstituts für Bergbau, Nr. 773, 1992.

4. Breer, Wolfgang ; Goetze, Wilhelm: Mitgefahrene und nachgefahrene Abbaustrecken im britischen Steinkohlenbergbau. In: Gluckauf 112 (1976), Nr. 2, S.70-75. der Schichten im Hangenden und Belastung des Streckenbegleitdamms in Abbaubegleitstrecken. Konferenz-Beitrдge, XXI. Winterschule für Gebirgsmechanik, Zakopane 1998.

5. Geffroy, Horst-Jürgen: Vergleich der verschiedenen Begleitdämme in einer Abbaustrecke. In: Gluckauf 108 (1972), Nr. 22, .1015-1017.

6. Irresberger, Hermann: Gebirgsbeherrschung in Streb und Strecke bei grosser Teufe. In: Gluckauf 116 (1980), Nr. 5, S.195-200.

7. Jacobi, Oskar: Praxis der Gebirgsbeherrschung. Essen: Verlag Glückauf, 1976.

8. Kammer, Willi ; Schroer, Diethelm ; Ingenabel, Kurt: Geringe Konvergenz durch einen Streckenbegleitdamm aus Anhydrit. In: Glückauf 108 (1972), Nr. 21, S.980-982.

9. Kammer, Willi: Grösserer Nutzquerschnitt durch starre Streckenbegleitdämme. In: Gluckauf 108 (1972), Nr. 22, S.1018-1020.

10. Pursek, s.: Messungen der Konvergenz, Aufblatterung der Schichten im Hangenden und Belastung des Streckenbegleitdamms im Abbaubegleitstrecken. Konferenz-Beitrage, XXI. Winterschule fur Gebirgsmechanik, Zakopane 1998.

11. Prusek, S.: Untertagemessungen in Abbaubegleitstrecken der Bruchstreben. Konferenz-Beiträge, XXII. Winterschule für Gebirgsmechanik, Karpacz 1999.

12. Prusek, S.: Ausgewälte Ergebnisse von Untertagemessungen in Abbaubegleitstrecken. In: Przegl ad Gorniczy 1999, Nr. 11.

13. Prusek, S.: Einfluss der Streckenbegleitdamme auf die Erhaltung von Abbaubegleitstrecken in Bruchbauraumen. Konferenz-Beiträge, XXIV. Winterschule für Gebirgsmechanik, Ladek Zdroj 2001.