С точки зрения обеспечения автономности в работе предпочтительным является использование пробоотборников с пневматическим или гидравлическим приводом. Однако, существующие конструкции подобных устройств реализуют главным образом вибрационный способ погружения керноприемной трубы в грунт, что негативно сказывается на качестве получаемой пробы. Как следствие она не отражает естественные свойства массива и не может быть использована для достоверной оценки его физико-механических свойств.
Отечественный и зарубежный опыт проведения работ показывает, что достаточное соответствие свойств грунта в пробе массиву наблюдается при частоте генерируемых ударов не более 1 Гц. Требуемую частоту ударов обеспечивает применение пробоотбор-ников с механическим приводом ударного узла. В подобных устройствах для подъема бойка в верхнее положение, как правило, используется грузовой канат с судовой лебедки. Движение вниз происходит под собственным весом бойка. Несмотря на очевидные преимущества, к которым следует отнести простоту конструкции и возможность регулирования в широком диапазоне параметров забивки: массы бойка, высоты его подъема, частоты нанесения ударов, применение пробоотборников этого типа характеризуется значительными затратами времени на бурение скважин вследствие малой ударной мощности.
В связи с этим, актуальным является разработка пробоотборника, обеспечивающего небольшую частоту, но вместе с тем повышенную энергию генерируемых ударов. За основу при разработке взята схема снаряда, предложенная и запатентованная на кафедре технологии и техники геологоразведочных работ ДонНТУ [1].
Пробоотборник (рис.1) состоит из ударного узла, включающего поршень-боек 1, наковальню 2 и проходящий через них полый шток 3, который с одной стороны связан канатом с судовой лебедкой, с другой – заканчивается синхронизирующим узлом, имеющим гибкую связь с обратным клапаном 4, и керноприемной трубы 5 с башмаком 6. Возвратно-поступательным перемещением штока подкачивают жидкость в рабочую полость 7, заставляя подниматься боек. По достижении им крайнего верхнего положения открывается обратный клапан в пневмокамеру 8. В результате под действием гидростатического давления и собственного веса происходит перемещение поршня-бойка до ударного взаимодействия с наковальней, которое сопровождается перетоком жидкости из рабочей через буферную 9 в пневматическую камеру.
В ходе теоретических исследований разработана математическая модель движения поршня-бойка на рабочем ходе, основанная на решении уравнения Бернулли для неустановившегося потока реальной жидкости [2]:
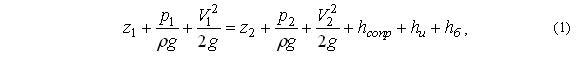
где p1, p2 – давление жидкости в сечениях I-I и II-II, Па; V1, V2 – скорость движения жидко-сти в сечениях, м/с; z1, z2 – удаление соответствующего сечения от нулевой плоскости, м (принимается, что нулевая плоскость совпадает с сечением I-I);
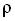– плотность рабочей жидкости, кг/м3; g – ускорение силы тяжести, м/с2; hсопр – потери напора при перетоке жидкости из рабочей камеры в пневмокамеру, м; hи – суммарный инерционный напор жидкости, м; hб – напор, обусловленный движением поршня-бойка, м.
Значения геометрического, пьезометрического и скоростного напоров для выбранных сечений приведены в табл.1. В ней S – величина рабочего хода поршня-бойка, м; l1, l2 – длина соответственно буферной камеры и аккумулирующей полости пневмокамеры, м; Н – глубина акватории, м;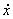 
– текущее значение скорости поршня-бойка, м/с; pк – давление воздуха в пневмокамере (Па), которое подчиняется зависимости
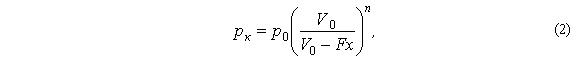
где p0 – начальное давление в пневмокамере, Па; V0– начальный объем воздушной полости пневмокамеры, м3; F – площадь поршня-бойка, м2 (определяется как
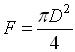, где D – диаметр поршня-бойка, м); х – текущая координата поршня-бойка при движении на рабо-чем ходе, м; n – показатель адиабаты (для воздуха принимают 1,41).
Из условия неразрывности потока жидкости имеем:
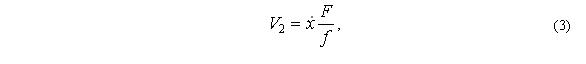
где f – площадь поршня пневмокамеры, м2 (определяется как
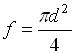, где d – диаметр поршня в пневмокамере, м.)
С учетом значений напоров в рассматриваемых сечениях уравнение (1) примет вид
Потери напора при перетоке жидкости из рабочей камеры в пневмокамеру слагаются из потерь по длине и в местных сопротивлениях.
Потери по длине определяются по формуле Дарси-Вейсбаха:
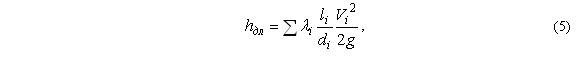
где
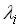– коэффициент гидравлического трения на i-том участке движения жидкости.
Применительно к расчетной схеме имеем:
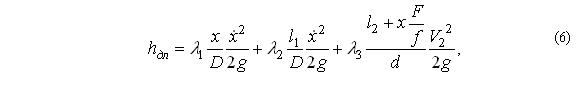
В этом выражении первое слагаемое учитывает потери напора на величине хода поршня-бойка, второе – в буферной камере, третье – в пневмокамере.
Величина
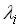зависит от режима движения жидкости, который определяется числом Рейнольдса:
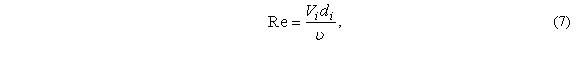
где
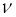– кинематическая вязкость, м2/с.
При Re>2300 наблюдается турбулентный режим течения жидкости, для которого коэффициент гидравлического трения определяют по формуле Блазиуса (для гладких труб):
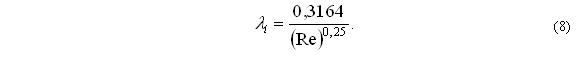
Если Re<2300 , то для ламинарного режима течения жидкости имеем:
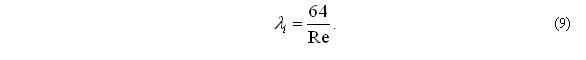
Считая, что скорости движения жидкости в рабочей полости и буферной камере приблизительно одинаковы, используя зависимости (7) и (8), преобразуем выражение (6) для турбулентного режима движения жидкости:
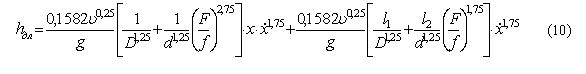
Если режим движения жидкости ламинарный, то с учетом зависимости (9) применительно к нашей схеме выражение (6) примет вид:
Потери напора в местных сопротивлениях определяются по формуле Вейсбаха:
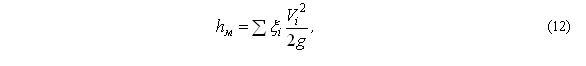
где Vi – скорость жидкости после прохода через местное сопротивление, м/с;
– коэффициент местных потерь.
По расчетной схеме выделяем местные сопротивления: на входе в шток, на выходе из штока и обратный клапан в пневмокамеру. Используя уравнение неразрывности потока жидкости, выражение (12) преобразуем:
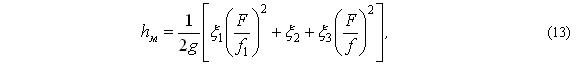
где f1 – площадь живого сечения в штоке диаметром d1, м2.
Согласно рекомендациям [3] коэффициенты местных сопротивлений
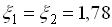(сопротивление при входе и истечении из трубы), 
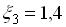(тарельчатый клапан).
Инерционный напор жидкости определяется по выражению:
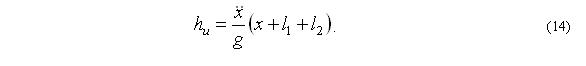
Для определения напора, обусловленного движением поршня-бойка, используем зависимость:
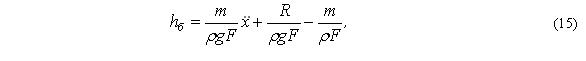
где m – масса поршня-бойка, кг; R – сила трения в цилиндре ударного узла, Н.
Подставим выражения (2), (10), (13), (14) и (15) в уравнение (4) и получим уравнение, описывающее движение поршня-бойка пробоотборника на рабочем ходе при турбулентном режиме течения жидкости:
где С1, А1, В1, D1 – сокращающие обозначения, равные
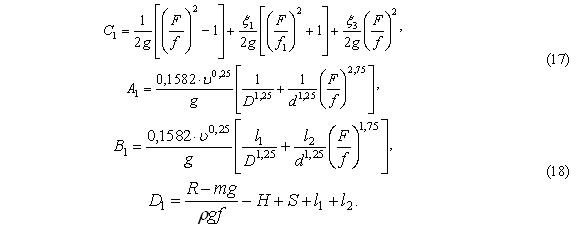
Для описания движение поршня-бойка при ламинарном режиме течения жидкости будем использовать уравнение, которое получим после подстановки в (4) зависимостей (2), (11), (13), (14) и (15):
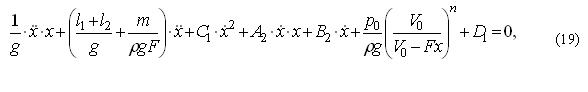
где А2, В2 – сокращающие обозначения, равные
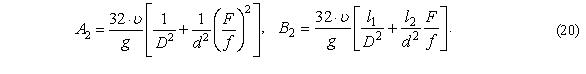
Решение уравнений (16) и (19) выполнялось численным методом Рунге-Кутта с помощью специально разработанной программы на языке Turbo Pascal 7.0.
Анализ математической модели позволяет сделать следующие выводы.
1. Движение поршня-бойка на рабочем ходе происходит под действием гидростатического давления столба жидкости (фактически это глубина применения пробоотборника) и собственного веса.
2. Препятствуют перемещению сила трения, перепад давления в местных сопротивлениях и давление в пневмокамере. Сила трения характеризуется постоянной величиной, в расчетах принималась равной половине массы поршня-бойка. Перепад давления в местных сопротивлениях напрямую зависит от скорости движения при перетоке жидкости из рабочей через буферную в пневматическую камеру пробоотборника. Чем больше текущая скорость поршня-бойка, а значит и скорость движения жидкости, тем существеннее влияние гидравлических сопротивлений. Давление в пневматической камере будет возрастать по мере притока жидкости в аккумулирующую полость, следовательно, затормаживать движение поршня-бойка на рабочем ходе.
Данные выводы подтверждаются результатами расчетов, которые были проведены для различных конструктивных и технологических параметров.
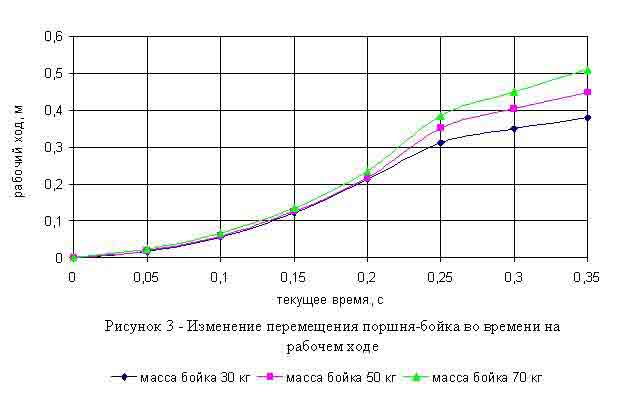
В начале перемещения поршня-бойка перепад сил является максимальным в пользу разгоняющих, поэтому для движения характерно наибольшее ускорение. При глубине мо-ря 20 м этот период занимает от 0,02 до 0,05 с (рис.2). При этом начало перемещения поршня-бойка сопровождается ламинарным режимом движения жидкости при ее перетоке.
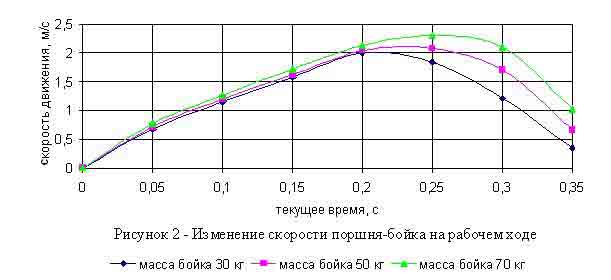
При дальнейшем перемещении поршня-бойка за счет увеличения сил сопротивления значение ускорения становится меньшим, но скорость поршня-бойка все равно возрастает, достигая максимума. Для бойка массой 30 кг максимум скорости приходится на текущее время 0,22 с, массой 50 кг – 0,24 с, массой 70 кг – 0,26 с. Для этого периода характерен турбулентный режим течения жидкости.
После чего движение поршня-бойка носит замедленный характер в силу того, что трение, перепад давления в местных сопротивлениях и давление в пневмокамере становится большим сил, участвующих в разгоне.
Зная, какая величина текущего времени соответствует максимальному значению скорости движения поршня-бойка по графику зависимости перемещения от времени (рис.3), можно определить оптимальный рабочий ход. Для бойка массой 30 кг он составит 0,22 м, массой 50 кг – 0,35 м, массой 70 кг – 0,40 м. Именно при этих значениях рабочего хода мы можем получить наибольшую энергию удара, что приведет к увеличению углубки керноприемной трубы за единичный удар и ускорит процесс пробоотбора.
На основании выполненных теоретических исследований разработана конструкция забивного пробоотборника диаметром 89 мм и выполнена проработка схемы установки для бурения инженерно-геологических скважин на морском дне.
