Целью данного исследования является определение напряженно-деформированного состояния (НДС) моделей системы «ствол – горизонтальная выработка» при взаимодействии крепления со слоистым деформативным массивом [1]. В качестве метода исследования использован метод конечных эле-ментов (МКЭ), программная реализация которого базируется на профессио-нальном расчетном комплексе Structure CAD for Windows, version 7.31 R.4 (SCAD), который имеет значительную теоретическую разработку и практиче-скую апробацию [1, 2].

Следует отметить, что проведение математического  моделирования выполнено в упругой постановке, что несколько снижает точность полученных результатов, так как известно, что породный массив на больших глубинах дефор-мируется в нелинейной области [3]. Однако упругая постановка вычислитель-ного эксперимента позволяет определить основные тенденции деформирования сложной системы «ствол – горизонтальная выработка» и характер влияния слоистости на общее НДС модели.

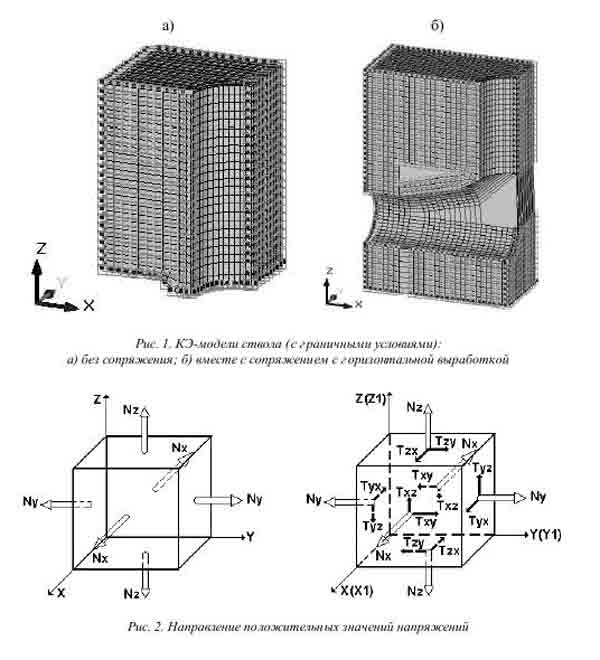
Для проведения численных расчетов созданы две конечно-элементные мо-дели (КЭ-модели, (рис. 1), которые являются континуальными на основе объ-емных конечных элементов. В качестве базового применялся КЭ библиотеки SCAD элемент 36 (8-узловой изопараметрический конечный объемный элемент задачи теории упругости), который наиболее соответствует геометрии модели и позволяет получить точные результаты. Тип КЭ, который применен в расчетах, определяется формой, функциями, которые определяют зависимость между пе-ремещениями в узлах КЭ и узлов системы, физическим законом, который опре-деляет зависимость между внутренними усилиями и внутренними перемеще-ниями, и набором параметров (жесткостей), которые входят в описание этого закона и так далее. Все узлы и элементы схемы нумеруются. Номера, которые присвоены КЭ, следует трактовать только как имена, которые позволяют сделать необходимые ссылки в процессе расчета.

Таким образом, дискретизацию модели можно считать  оптимизированной по параметру количества конечных элементов и их отношения  к объему модели, что в дальнейшем положительно влияет на сходимость решения  мультифрон-тальным методом с автоматическим способом оптимизации ширины ленты (точность разложения матрицы 1·10-6).

Правило знаков для перемещений принято таким  образом, что линейные перемещения  положительны, если они направлены в сторону возрастания соответствующей координаты, а углы поворота положительны, если они отвечают правилу правого винта.

Правило знаков для напряжений приняты следующие. Компоненты объемного напряженного состояния определяются для элементарного параллелепипеда, который выделен вокруг точки действия напряжений. Кроме того, устанавливаются нормальные напряжения Nx (σx), Ny (σy), Nz (σz) и касательные напряжения Txy (τxy), Tyx (τyx), Txz (τxz), Tzx (τzx), Tzy (τzy), Tyz (τyz) (обозначение компонент в комплексе SCAD). С учетом закона парности касательных напряжений

(Txy=Tyx, Txz=Tzx, Tyz=Tzy) выводятся лишь значения трех из них: Txy, Txz, Tyz.

На рис. 2 показаны положительные значения направлений напряжений и данного наименования соответствующих осей, вдоль которых  они направлены, а также плоскостей, в которых они действуют.  
 

Созданные пространственные модели из объемных элементов для исследования НДС ствола и сопряжения (рис. 1) наиболее полно отражает следующие особенности реальной конструкции:

– влияние пространственного  фактора на формирование напряженного состояния, то есть влияние третьей  компоненты σу на компоненты σх та σz;

– наиболее полное воссоздание взаимодействия железобетонного  крепления с грунтовым массивом.

Разработка этих двух моделей также обусловлена  проведением исследования влияния граничных условий, расположенных по нижней грани модели. В стандартных моделях, не учитывающих влияние сопряжения с горизонтальной выработкой на деформирование общей системы и ствола в частности, в качестве граничных условий по нижней грани КЭ-модели устанавливают запреты перемещений по всем трем степеням свободы. Однако, в реальной ситуации деформирования данной системы об отсутствии перемещений не приходится говорить, так как деформативность сопряжения явно конечна и позволяет стволу и окружающему массиву развивать как горизонтальные, так и вертикальные перемещения. Поэтому результаты расчета КЭ-модели, представленной на рис. 1., а, являясь стандартными, будут сравниваться с результатами расчета общей системы «ствол – горизонтальная выработка», что позволит выяснить, насколько достоверными являются результаты расчета модели ствола без учета сопряжения.

Размеры расчетной  области составляют: длина (по горизонтальной оси x ) – 13,4 м; высота (по вертикальной оси z ) – 48,0 м, ширина (по горизонтальной оси y) – 15 м. Количество КЭ в моделях: 1-ой – 15 296, 2-ой – 33 114; количество узлов: 1-ой – 17 473, 2-ой – 37 193; количество степеней свободы: 1-ой – около 52 419, 2-ой – около 111 579. Данная задача может считаться задачей средней размерности (количество КЭ – до 50 тысяч).

Объем конечного  элемента в моделях колеблется в  пределах от 0,12 м3 до 3 м3 (специальные  КЭ в месте сопряжения), что для  модели таких размеров достаточно, чтобы сходимость решения и точность результатов были достаточно высоки [2]. На рис. 3. представлены фрагменты второй КЭ-модели, в которой массив фрагментирован и для иллюстрации соединения частей модели показано лишь ее крепление.  
 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. SCAD для пользователя [Текст] / В. С. Карпиловский, Э. З. Криксунов, А. В. Перельмутер и др. – К.: ВВП «Компас», 2000. – 332 с.

2. Перельмутер, А. В. Расчетные модели сооружений и возможность их анализа [Текст] / А. В. Перельмутер, В. И. Сливкер. – К.: Сталь, 2002. – 600 с.

3. Алексеев, А. Д. Предельное состояние горных пород [Текст] / А. Д. Алексеев, И. В. Недодаев. – К.: Наукова думка, 1982. – 200 с.