Моделирование с отклонением от круглости при бурении глубоких отверстий
До Хан Чин, Мун Чал Йун, Санг Бо Сим
Магистратура факультета машиностроения, Национальный университет Пакуйонг, Пусан, Южная Корея
Факультет машиностроения, Национальный университет Пакуйонг, Пусан, Южная Корея
Перевод с английского: Якубцова Н. В
Библиотека
Источник: http://www.elsevier.com/wps/find/journaldescription.cws_home/525017/description#description
Краткий обзор статьи
Здесь представлено моделирование процесса бурения глубоких скважин, описаны его характеристики. Также установлены параметры сечения при глубоком бурении, а достоверность его геометрической модели была подтверждена экспериментальным путем в ходе операции глубокого бурения. В данном исследовании была представлена гармоническая геометрическая сферическая модель с параметрами гармонической функции. Такая зависимость также используется для обеспечения физических смыслов для гармоничных граней, сформированных предложенной моделью отклонения от круглости для сечения глубокого сверления, особенно тех, которые появились в результате ошибочного смещения шпинделя устройства глубокого сверления. В общем, разрез отверстия с произвольным множественным количеством граней может быть просчитан. При практических экспериментах было также измерено сечение скважины с 2-6 гранями. Наиболее часто измерениям подвергались 3 и 5-граневые сечения. Надежность предложенной гармонической модели была подтверждена теоретическим и экспериментальным путем, большим количеством действительных расчетов сечения скважины и результатами экспериментов, совершенных путем сверления глубоких отверстий. Этот новый метод моделирования поможет достигнуть нужного понимания углубленного анализа допустимого отклонения цилиндрического отверстия в процессе глубокого сверления.
Ключевые слова: сверло для глубокого сверления; дробная частота; сечение грани; отклонение от круглости; смещение шпинделя.
1. Введение
Метод моделирования при сверлении глубоких отверстий часто применяется в различных видах производства, таких как машиностроение для бурения, атомная энергетика, нефтегазовая сфера, авиакосмическая промышленность. Моделирование процесса сверления глубоких отверстий, учитывая ошибочные смещения шпинделя, является необходимым для анализа формы граней и их допустимого отклонения при круговом и цилиндрическом разрезе. Данный тип моделирования отклонения от круглости также стал популярен в научной литературе, и далее рассмотрены обзоры некоторых работ по данной теме. Общеизвестно, что инструменты требуют высокого внимания к качеству, а также точного измерения и учета допустимых отклонений. Таким образом, результат изучения этих параметров, полученный экспериментальным путем, был проверен инструментом из легированной инструментальной стали при бурении скважины с применением установок глубокого бурения при нескольких типах условий резки. Этот результат был сравнен с результатами теоретического моделирования. Как правило, глубокими называются скважины, где коэффициент соотношения глубины к диаметру равен более 20. Глубокое бурение применяется для проходки скважин данного типа.
Множество ученых посвятили свои работы изучению глубокого сверления. Сакума и его научная группа экспериментальным путем изучали разрез глубокой скважины и образующий ее механизм. Этот результат применяется в сфере разработки оптимального дизайна режущего элемента сверла для глубокого бурения, который генерирует наименьшую силу резания. Также Саваб и его научная группа установили взаимодействие между ошибочным радиальным смещением шпинделя и полученным в результате сечением для токарной обработки после механической обработки. Дамир разработал примерную гармоническую модель для определения амплитудных спектров разреза грани с гармоническим отклонением от круглости при различных процессах механической обработки. Ученые Чо и Ту также разработали модель грани с отклонением от круглости обрабатываемых деталей для анализа допустимого отклонения. В своих работах они показали, что ошибочное смещение шпинделя может стать причиной подобного разреза с отклонением от округлости. Например, повторяемость ошибочного смещения шпинделя с тремя выступами может стать причиной 3-граневого кругового разреза. Этот анализ, тем не менее, был также направлен на изучение ошибочных смещений целого кратного количества вращений шпинделя, а также рассматривал важность дробной частоты ошибочных смещений и вибрации инструмента при вращательном движении. К тому же много исследователей ведут исследования характеристик отверстия при условии отклонения от круглости [5–11]. При исследовании данного вопроса была изучена новая модель глубокого сверления при условии отклонения от круглости и ее характеристики. Надежность модели была доказана в результате сравнения теоретических и практических результатов. В более полном объеме характеристики глубокого сверления при использовании легированной инструментальной стали, а также точность скважины были установлены с помощью теоретических подсчетов и экспериментальных измерений в ходе глубокого сверления с применением числового программного управления типа CNC. Выступ кулачка, используемый для глубокого сверления, изображен на Рис. 1.
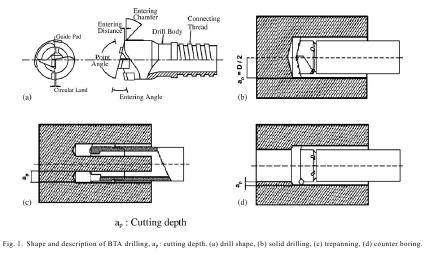
|
2. Моделирование с отклонением от круглости при глубоком сверлении.
Модель сечения с отклонением от круглости при глубоком сверлении была разработана для описания действия ошибочного смещения шпинделя на сечение с отклонением от круглости для пробуренной скважины. Рис.2 показывает модель образования отверстия при глубоком сверлении при смещении шпинделя устройства глубокого сверления. Сечение грани с отклонением от круглости является внутренней линией просверленного объекта в данной плоскости, и это круговое сечение расположено в плоскости перпендикулярной оси цилиндра. В отношении цилиндра сечение расположено на поверхности пересеченной любой плоскостью, проходящей через общий центр. Если в стержне инструмента для глубокого сверления присутствует смещение шпинделя, то скоро его вращательное движение становится постоянным. Центр инструмента для глубокого сверления вращается по круговой или овальной траектории стационарного состояния. При начальном положении вращения беспорядочное пересечение центра может также иметь место.
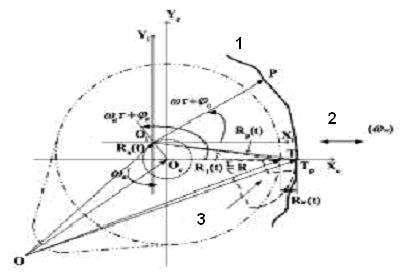
|
Рис.2 Сечение круглой грани, образованной ошибочным смещением инструмента глубокого сверления.
|
1. Сечение образованного отверстия; 2. Обрабатываемая деталь; 3. Инструмент глубокого сверления.
|
Принимая во внимание движение инструмента глубокого сверления при стабильном вращении и траекторию центра инструмента, имеющую круговой характер, идеализированная гармоническая модель может иметь вид, показанный на Рис.1. На Рис.2 точка Oc – это центр абсолютной координаты, а Oi – это мгновенный центр инструмента глубокого сверления с ошибочным смещением шпинделя, который вращается по гармоническому кругу. Радиус Ra (t,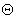 )который является радиусом траектории, вращается с частотой вращения
)который является радиусом траектории, вращается с частотой вращения  и его радиус равен Oc Oi. Векторное представление от точки Oc к точке Oi может быть представлено следующим образом:
и его радиус равен Oc Oi. Векторное представление от точки Oc к точке Oi может быть представлено следующим образом:
где j это мнимая единица. Но:
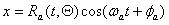
|
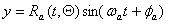
|
ТочкаTp это фиксированное местоположение инструмента глубокого сверления и она обусловлена вращением центра инструмента и вибрации обрабатываемой детали с амплитудой Rw(t), в направлении х по причине плохого закрепления. На Рис.2 расстояние 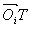 , от Oi к T, может быть Rl(t) а расстояние между Oi и Tp может быть представлено как Rp(t). Инструмент глубокого сверления вращается с радиусом Rp(t) и его частота вращения
, от Oi к T, может быть Rl(t) а расстояние между Oi и Tp может быть представлено как Rp(t). Инструмент глубокого сверления вращается с радиусом Rp(t) и его частота вращения 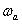 центр расположен в точке Oi. Таким образом, правая точка радиуса Rp(t) соответствует реальному сечению расстояния по радиусу R1(t), принимая во внимание ошибочное смещение шпинделя. Также перемещение Tp, учитывая обрабатываемую деталь, является перемещением смещения шпинделя в направлении x с амплитудой
центр расположен в точке Oi. Таким образом, правая точка радиуса Rp(t) соответствует реальному сечению расстояния по радиусу R1(t), принимая во внимание ошибочное смещение шпинделя. Также перемещение Tp, учитывая обрабатываемую деталь, является перемещением смещения шпинделя в направлении x с амплитудой  и частотой
и частотой 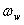 . Определено, что конечное сечение отклонения от округлости может быть вызвано сочетанием движением смещения оси шпинделя, который вращается по радиусу вокруг абсолютного центра, и низким сопротивлением вибрации обрабатываемой детали. Эти конечные траектории, Tp, являются сечением формы, просверленной сверлом глубокого сверления. Таким образом, уравнение этой траектории может быть представлено следующим образом [7]:
. Определено, что конечное сечение отклонения от округлости может быть вызвано сочетанием движением смещения оси шпинделя, который вращается по радиусу вокруг абсолютного центра, и низким сопротивлением вибрации обрабатываемой детали. Эти конечные траектории, Tp, являются сечением формы, просверленной сверлом глубокого сверления. Таким образом, уравнение этой траектории может быть представлено следующим образом [7]:
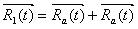
|
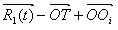
|
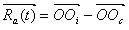
|

|

|
Условие, когда некоторое произвольное положение лезвия инструмента глубокого сверления совпадает с позицией в той же плоскости после одного вращения может быть определено как сечение закрытой грани и представлено следующим образом:
но
Если положение после одного вращения не совпадает в одной плоскости с позицией до вращения, тогда это не закрытая грань. Это является причиной прерывистого сечения. Но если учесть, что величины 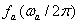 и
и 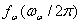 являются целыми числами, тогда это указывает на сечение закрытой грани. Кроме того, амплитуда траектории сечения грани R1(t) может быть представлена следующим образом:
являются целыми числами, тогда это указывает на сечение закрытой грани. Кроме того, амплитуда траектории сечения грани R1(t) может быть представлена следующим образом:
Используя дискретное фурье-преобразование в частотной области, можно представить следующее:
где N: количество отбора проб, fk: количество граней (0, 1, ...,n-1),  амплитуда i-ного вектора радиуса пробы, R1(fk): комплексная амплитуда компонента грани k.
амплитуда i-ного вектора радиуса пробы, R1(fk): комплексная амплитуда компонента грани k. Используя дискретную форму уравнения 7, с помощью собственных форм колебаний 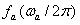 и
и  или их комбинации в частотной области, генерируется частота сечения грани.
или их комбинации в частотной области, генерируется частота сечения грани.
Библиотека



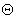 )который является радиусом траектории, вращается с частотой вращения
)который является радиусом траектории, вращается с частотой вращения  и его радиус равен Oc Oi. Векторное представление от точки Oc к точке Oi может быть представлено следующим образом:
и его радиус равен Oc Oi. Векторное представление от точки Oc к точке Oi может быть представлено следующим образом:

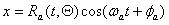
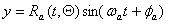
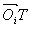 , от Oi к T, может быть Rl(t) а расстояние между Oi и Tp может быть представлено как Rp(t). Инструмент глубокого сверления вращается с радиусом Rp(t) и его частота вращения
, от Oi к T, может быть Rl(t) а расстояние между Oi и Tp может быть представлено как Rp(t). Инструмент глубокого сверления вращается с радиусом Rp(t) и его частота вращения 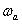 центр расположен в точке Oi. Таким образом, правая точка радиуса Rp(t) соответствует реальному сечению расстояния по радиусу R1(t), принимая во внимание ошибочное смещение шпинделя. Также перемещение Tp, учитывая обрабатываемую деталь, является перемещением смещения шпинделя в направлении x с амплитудой
центр расположен в точке Oi. Таким образом, правая точка радиуса Rp(t) соответствует реальному сечению расстояния по радиусу R1(t), принимая во внимание ошибочное смещение шпинделя. Также перемещение Tp, учитывая обрабатываемую деталь, является перемещением смещения шпинделя в направлении x с амплитудой  и частотой
и частотой 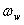 . Определено, что конечное сечение отклонения от округлости может быть вызвано сочетанием движением смещения оси шпинделя, который вращается по радиусу вокруг абсолютного центра, и низким сопротивлением вибрации обрабатываемой детали. Эти конечные траектории, Tp, являются сечением формы, просверленной сверлом глубокого сверления. Таким образом, уравнение этой траектории может быть представлено следующим образом [7]:
. Определено, что конечное сечение отклонения от округлости может быть вызвано сочетанием движением смещения оси шпинделя, который вращается по радиусу вокруг абсолютного центра, и низким сопротивлением вибрации обрабатываемой детали. Эти конечные траектории, Tp, являются сечением формы, просверленной сверлом глубокого сверления. Таким образом, уравнение этой траектории может быть представлено следующим образом [7]:
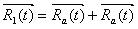
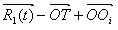
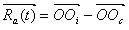



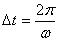
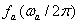 и
и 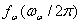 являются целыми числами, тогда это указывает на сечение закрытой грани. Кроме того, амплитуда траектории сечения грани R1(t) может быть представлена следующим образом:
являются целыми числами, тогда это указывает на сечение закрытой грани. Кроме того, амплитуда траектории сечения грани R1(t) может быть представлена следующим образом:


 амплитуда i-ного вектора радиуса пробы, R1(fk): комплексная амплитуда компонента грани k.
амплитуда i-ного вектора радиуса пробы, R1(fk): комплексная амплитуда компонента грани k. 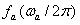 и
и  или их комбинации в частотной области, генерируется частота сечения грани.
или их комбинации в частотной области, генерируется частота сечения грани.