
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СХЕМ ЗАМЕЩЕНИЯ СИНХРОННЫХ МАШИН ПРИ ПРЕДСТАВЛЕНИИ ОБМОТКИ ВОЗБУЖДЕНИЯ МНОГОКОНТУРНОЙ ЦЕПЬЮ
Викладені основні положення методу експериментального визначення параметрів заступних еквівалентних схем синхронних машин, в яких обмотка збудження представлена багатоконтурним колом. Метод засновано на даних одночасної реєстрації струмів в обмотках статора і збудження при раптових трифазних коротких замиканнях на затисках електричної машини. Наведені результати досліджень для промислового турбогенератора ТВВ-160.
Изложены основные положения метода экспериментального определения параметров эквивалентных схем замещения синхронных машин, в которых обмотка возбуждения представлена многоконтурной цепью. Метод основан на данных одновременной регистрации токов в обмотках статора и возбуждения при внезапных трехфазных коротких замыканиях на выводах электрической машины. Приводятся результаты исследований для промышленного турбогенератора ТВВ-160.
Введение

Рисунок 1 - Схема замещения с учетом различной магнитной связи между контурами
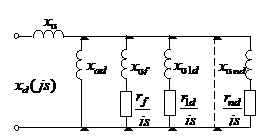
Рисунок 2 - Схема замещения СМ по продольной оси
В настоящее время для расчета переходных процессов в синхронных машинах
(СМ) используются схемы замещения, в которых предполагается, что цепи обмотки
статора, возбуждения и демпферных контуров имеют магнитную связь только через основное
магнитное поле взаимной реактивностью ![]() (рис. 1).
(рис. 1).
Такие Т –образные схемы замещения с достаточной точностью отражают переходные процессы в обмотке статора, но приводят к значительным (иногда даже неприемлемым) погрешностям при расчетах токов в обмотке возбуждения.
Поэтому, модель СМ в виде многоконтурных схем замещения общепринятого вида в сочетании с полными уравнениями Парка-Горева не обладает достаточной гибкостью и не может быть использована для уточненного исследования переходных процессов в обмотке возбуждения генераторов (ОВГ).
В последнее время появились работы, посвященные построению схем замещения уточненной (рис. 2) структуры [2, 3].
Они более достоверны с физической точки зрения, поскольку в них учитывается различие взаимоиндуктивной магнитной связи между обмотками статора, возбуждения и эквивалентными контурами демпферной системы ротора. Однако способы определения параметров таких схем замещения еще достаточно не разработаны и, практически, отсутствует фактический материал, позволяющий использовать их в расчетах переходных процессов. Применение метода конечных элементов к синтезу подобных эквивалентных схем замещения не всегда приводит к физически обоснованным результатоам. Полученное в [3] индуктивное сопротивление рассеяния ОВГ имеет отрицательное значение. Погрешности в определении тока ротора при исследовании переходных процессов, например, при коротких замыканиях, объясняются, в частности, тем, что строго ОВГ нельзя представить одноконтурной цепью [4].
В [4] предложен способ синтеза схем замещения СМ вида, показанного на рис. 1, при представлении ОВГ самостоятельной многоконтурной цепью. Метод основан на одновременной регистрации токов в обмотках статора и ротора в опыте затухания постоянного тока, проводимого на неподвижной машине. При этом на процедуру обработки исходных данных накладываются жесткие ограничения по количеству экспонет в токах статора и ротора, их постоянных времени затухания и др. Исследования по использованию предложенного в [4] способа показали, что, в большинстве случаев, он не дает удовлетворительных результатов.
Сотрудниками Сибирского НИИ энергетики (Россия) предложены и получены более сложные структуры эквивалентных схем замещения турбогенераторов, также учитывающих различную взаимоиндуктивную связь между контурами, расположенными на роторе. Основной отличительной особенностью таких схем замещения является представление демпферной системы машины по продольной и поперечной осям ротора в виде основного демпферного контура, охватывающего магнитный поток взаимоиндукции между статором и ротором, и ряда локальных контуров, охватывающих магнитные потоки рассеяния и обмотки возбуждения. В этом случае обмотка возбуждения генератора, его демпферная система и цепи, отражающие взаимную индуктивную связь между ними характеризуются сложными зависимостями от скольжения высокого порядка (рис. 3).
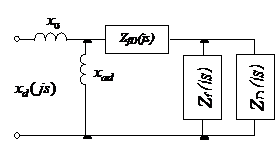
Рисунок 3 - Схема замещения СМ высокого порядка
Из выполненного анализа следует, что задача уточненного определения параметров эвивалентных схем замещения синхронных машин является актуальной.
Целью настоящей работы является разработка способа экспериментального определения параметров схем замещения СМ различных структур при представлении в них обмотки возбуждения многоконтурной цепью.

Рисунок 4 - Г-образная схема замещения при представлении ОВГ многоконтурной цепью
Аналогичная задача, но при представлении ОВГ одним контуром решалась в [5].
основные математические соотношения
Предлагаемый способ основан на использовании частотной
характеристики комплексного коэффициента распределения продольной составляющей
тока статора в ветви обмотки возбуждения ![]() . В соответствии с [5] указанная характеристика
определяется по данным обработки токов статора и ротора в опыте внезапного
трехфазного короткого замыкания на выводах синхронного генератора, работающего
на холостом ходу, следующим образом:
. В соответствии с [5] указанная характеристика
определяется по данным обработки токов статора и ротора в опыте внезапного
трехфазного короткого замыкания на выводах синхронного генератора, работающего
на холостом ходу, следующим образом:
![]() , (1)
, (1)
В (1) частотная характеристика проводимости со стороны
обмотки статора по продольной оси ротора![]() определяется по параметрам экспоненциальных
составляющих, аппроксимирующих периодическую слагаемую тока статора, в
соответсвии с рекомендациями ГОСТ 10169-77. Частотная характеристика
определяется по параметрам экспоненциальных
составляющих, аппроксимирующих периодическую слагаемую тока статора, в
соответсвии с рекомендациями ГОСТ 10169-77. Частотная характеристика ![]() проводимости
ветви ОВГ рассчитывается по параметрам экспонент, аппроксимирующих
апериодическую составляющую тока в обмотке возбуждения (
проводимости
ветви ОВГ рассчитывается по параметрам экспонент, аппроксимирующих
апериодическую составляющую тока в обмотке возбуждения (![]() ):
):
![]() . (2)
. (2)
По значениям частотной характеристики ![]() может быть синтезирована
любая из приведенных эквивалентных схем замещения. Применяемые для этого методы
основаны на условии адекватности только исходной характеристики и характеристики,
рассчитываемой по параметрам схемы замещения, т.е
может быть синтезирована
любая из приведенных эквивалентных схем замещения. Применяемые для этого методы
основаны на условии адекватности только исходной характеристики и характеристики,
рассчитываемой по параметрам схемы замещения, т.е ![]() . В этом случае обмотка возбуждения
при представлении ее одним контуром, в большинстве случаев отражается неверно.
Для более точного определения параметров схем замещения, учитывающих влияние
ОВГ, необходимо, чтобы в них характеристика
. В этом случае обмотка возбуждения
при представлении ее одним контуром, в большинстве случаев отражается неверно.
Для более точного определения параметров схем замещения, учитывающих влияние
ОВГ, необходимо, чтобы в них характеристика ![]() также соответствовала исходной, полученной в
опыте трехфазного короткого замыкания.
также соответствовала исходной, полученной в
опыте трехфазного короткого замыкания.
Следовательно, зная комплексные значения проводимости ![]() и коэффициента
токораспределения
и коэффициента
токораспределения ![]() , можно определить необходимую зависимость от
частоты результируещей проводимости ОВГ. Выполним это следующим образом:
, можно определить необходимую зависимость от
частоты результируещей проводимости ОВГ. Выполним это следующим образом:
![]() . (3)
. (3)
Такому действию соответствует эквивалентная схема замещения с вынесенной на зажимы источника ветвью намагничивания (Г – образная схема), приведенная на рис. 4.
Представим ветвь обмотки возбуждения в виде ряда параллельно включенных активно-индуктивных цепочек. Тогда результирующая проводимость, найденна по (3) может быть рассчитана по параметрам схемы замещения следующим образом:
![]() . (4)
. (4)
Таким образом, зная резульрующую проводимость ветви ОВГ ![]() можно определить
параметры отдельных контуров. Для этого можно использовать известные алгоритмы,
а также процедуры минимизации универсальных прикладных пакетов для ПЭВМ.
можно определить
параметры отдельных контуров. Для этого можно использовать известные алгоритмы,
а также процедуры минимизации универсальных прикладных пакетов для ПЭВМ.
Результирующая проводимость контуров, эквивалентирующих демпферную
систему![]() , в
соответствии с рис. 4 определяется следующим соотношением:
, в
соответствии с рис. 4 определяется следующим соотношением:
![]() . (5)
. (5)
Представляя демпферную систему как и ОВГ многоконтурной цепью, можно получить параметры отдельных ее контуров на основании равенства
![]() . (6)
. (6)
Схема замещения вида, приведенного на рис.4, удобна при использовании частотного метода расчета для аналитического описания электромагнитных переходных процессов. Она может быть также использована и при исследованиах, основанных на решении полных дифференциальных уравнений Парка-Горева.
Для синтеза параметров схемы замещения, Т – образного вида,
(рис. 1), при представлении ОВГ многоконтурной цепью результирующая проводимость
![]() должна
определяться с учетом известного индуктивного сопротивления рассеяния обмотки
статора
должна
определяться с учетом известного индуктивного сопротивления рассеяния обмотки
статора ![]() :
:
![]() , (7)
, (7)
где ![]() - проводимость схемы замещения, измеренная
относительно зажимов ветви намагничивания.
- проводимость схемы замещения, измеренная
относительно зажимов ветви намагничивания.
Тогда результирующая проводимость демпферных контуров
находится путем вычитания из проводимости ![]() проводимости ветви намагничивания и ОВГ:
проводимости ветви намагничивания и ОВГ:
![]() . (8)
. (8)
В соответствии с сотношениями (4) и (6) находятся параметры многоконтурных схем, эквивалентирующих соответственно ОВГ и демпферную систему в схеме, представленной на рис. 1.
Для нахождения результирующей проводимости ![]() в схеме, учитывающей
различную взаимную индуктивность между контурами, расположенными на роторе (
в схеме, учитывающей
различную взаимную индуктивность между контурами, расположенными на роторе (![]() ), выполняются
следующие расчетные процедуры.
), выполняются
следующие расчетные процедуры.
Определяется результирующая проводимость цепи, учитывающей
влияние контуров ОВГ, демпферной системы и известного сопротивления взаимоиндуктивности
![]() по соотношению
по соотношению
![]() . (9)
. (9)
Находится коэффициент участия тока в обмотке статора (в
сопротивлении ![]() в
ветви сопротивления взаимоиндукции
в
ветви сопротивления взаимоиндукции ![]()
![]() . (10)
. (10)
По известному коэффициенту ![]() и найденному значению
и найденному значению ![]() рассчитывается коэффициент
участия тока, протекающего в сопротивлении
рассчитывается коэффициент
участия тока, протекающего в сопротивлении ![]() в цепи ОВГ (
в цепи ОВГ (![]() ):
):
![]() . (11)
. (11)
Определяется зависимость от частоты результирующей проводимости, характеризующей влияние ОВГ.
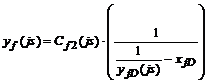 . (12)
. (12)
Тогда в соответствие со схемой замещения суммарная проводимость контуров, эквивалентирующих демпферную систему, рассчитывается следующим образом:
 . (13)
. (13)
Дальнейшие процедуры по определению параметров контуров, отражающих влияние ОВГ и демпферной системы аналогичны вышеописанным.
оЦЕНКА ЭФФЕКТИВНОСТИ ПРЕДЛОЖЕННОГО МЕТОДА
Для оценки эффективности разработанного в работе метода
экспериментального определения параметров эквивалентных схем замещения различных
структур при представлении ОВГ многоконтурной цепью были выполнены опыты
внезапного трехфазного короткого замыкания на выводах турбогенератора типа ТВВ
– 160. С целью определения ненасыщенных значений электромагнитных параметров
опыт проводился из режима холостого хода генератора при напряжении,
составляющем ![]() .
Исследования проводились для различных условий по аппроксимации периодической составляющей
тока в обмотке статора и апериодического тока в цепи обмотки возбуждения.
Оценивалось влияние числа и постоянных времени затухания экспоненциальных
составляющих, аппраксимирующих токи в статоре и роторе. Рассматривались
варианты с одинаковым и различным количеством экспонент в токах статора и
ротора, а также одинаковыми и различными дикриментами их затухания. При этом
определялись параметры схем замещения различных структур. Во всех случаях
принималось, что
.
Исследования проводились для различных условий по аппроксимации периодической составляющей
тока в обмотке статора и апериодического тока в цепи обмотки возбуждения.
Оценивалось влияние числа и постоянных времени затухания экспоненциальных
составляющих, аппраксимирующих токи в статоре и роторе. Рассматривались
варианты с одинаковым и различным количеством экспонент в токах статора и
ротора, а также одинаковыми и различными дикриментами их затухания. При этом
определялись параметры схем замещения различных структур. Во всех случаях
принималось, что ![]() ;
; ![]() . При синтезе схемы, приведенной на рис. 3,
индуктивное сопротивление взаимоиндукции
. При синтезе схемы, приведенной на рис. 3,
индуктивное сопротивление взаимоиндукции ![]() принималось независящим от частоты и равным
0,0065 о.е.
принималось независящим от частоты и равным
0,0065 о.е.

Рисунок 5 - Изменение тока в цепи ОВГ при трехфазном КЗ ТГ ТВВ - 160
При представлении ОВГ двухконтурной цепью и аппроксимации токов статора и ротора составляющими, имеющими разные постоянные времени затухания, были получены следующие параметры схемы замещения, показанной на рис. 4:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() .
.
Параметры схемы замещения Т – образного типа (рис. 1) в этом случае имеют следущие значения:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() .
.
Схеме с различной взаимной индуктивностью между контурами (рис.3), соответсвуют такие параметры роторных контуров:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Достоверность полученных параметров проверялась путем сопоставления результатов расчета тока в ОВГ по полным дифференциальным уравнения Парка-Горева с экспериментальными данными. Результаты приведены на рис. 5.
На этом же рисунке приведены результаты расчета при представлении обмотки возбуждения в обычной схеме замещения одним контуром.
Сопоставление результатов расчета при представлении ОВГ одним контуром (кривая 3) с экспериментальными данными (кривая 1) свидетельствует, об их неудовлетворительном совпадении. Погрешность расчета достигает 38,3 % в диапазоне времен до 0,1 с. Во временном диапазоне более 0,1 с погрешность несколько снижается и составляет 15 – 20 %.
Использование схем замещения при представлении ОВГ многоконтурной цепью (кривая 2) позволяет существенно (более чем в два раза) снизить ошибку в результатах расчета. В рассматриваемом случае максимальное несовпадение расчетных и экспериментальных данных не превышает 14,2 % в течение первых двух - трех периодов промышленной частоты. В остальном интервале наблюдения переходного поцесса погрешность не превышает 9%.
ВЫВОД
Предложенный метод экспериментального определения параметров эквивалентных схем замещения при представлении ОВГ многоконтурной цепью позволяет существенно уточнить математическую модель СМ при исследованиях переходных процессов в обмотке возбуждения.
Литература:
[1] Казовский Е.Я., Рубисов Г.В. Переходные процессы в синхронных машинах при анормальных режимах в энергосистеме. – СПб.: Наука, 1994. – 172 с.
[2] Рогозин Г.Г., Ларин А.М., Ларина И.И. Определение зависимости параметров эквивалентного демпферного контура турбогенератора от начального значения тока короткого замыкания // Электротехника. – 1999. - №12. – С. 14-17.
[3] Escarela-Pereze R., Campero-Littlewood E., Niewierowicz T., Hernandez-Anaya O. Unique Determination of One-Damper D-Axis Circuits of Synchronous Machines Using Finite-Element Simulations // IEEE Transactions on Magnetics, 2002. -Vol. 38. - №2. – P. 1245-1248.
[4] Сидельников А.В. Синтез схемы замещения синхронной машины при представлении обмотки возбуждения многоконтурной цепью // Электротехника. – 1983. - №7. – С. 25-28.
[5] Ларин А.М., Ткаченко А.А., Ларина И.И. Определение электромагнитных параметров обмотки возбуждения синхронного генератора из опытов внезапного трехфазного короткого замыкания // Електротехніка і Електромеханіка, 2005. - №2. – С. 32-34.