УДК 621.313.32.001.4.681.3
А.А. Ткаченко
Источник: Праці Луганського відділення Міжнародної Академії інформатизації, Луганськ: СНУ ім. Даля, 2005, №1. – стор. 49 – 53.
Запропоновано уточнену математичну модель, яку покладено в основу методики визначення сукупності електромагнітних параметрів синхронних машин з урахуванням багатоконтурності ротора за даними обробки перехідних функцій струмів раптового трифазного короткого замикання. Рис. 3, дж. 9.
Введение. Широкое внедрение средств вычислительной техники и разработка различных математических моделей переходных процессов в электрических машинах переменного тока (ЭМ) создают предпосылки для повышения точности методов экспериментального определения их электромагнитных параметров. Для этой цели наиболее часто используют опыты внезапного трехфазного короткого замыкания (ВКЗ).
Процедура нахождения значений параметров синхронных машин (СМ) из опытов ВКЗ регламентирована рекомендациями международной электротехнической комиссии [1] и действующим в Украине и странах СНГ ГОСТ 10169-77 [2]. Однако найденные по стандартной методике из опытов ВКЗ значения электромагнитных параметров имеют существенный разброс даже при обработке исходных данных с помощью ЭВМ [3]. Вопросам точности экспериментального определения параметров из опытов ВКЗ посвящено достаточное количество работ [4-7]. В [4,5] сделана попытка выяснить причины погрешностей в допущениях при упрощенном решении дифференциальных уравнений СМ, на которых основана стандартная методика и при получении самих уравнений. В качестве причин разброса в [6,7] выявлено влияние допущений, связанных с пренебрежением медленным вращением апериодической составляющей и неучетом второй гармоники тока ВКЗ. Сформулированы предложения по уточнению стандартной методики путем контроля точности проведения экспериментов и определения параметров отдельно по значениям токов в каждой фазе. Во всех рассматриваемых случаях предполагается, что СМ кроме обмотки возбуждения (ОВ) имеет только по одному демпферному контуру по каждой оси несимметрии ротора.
При этом не оценивается влияние параметров СМ по поперечной оси на токи в фазах при ВКЗ. Как показано в [8], такое влияние всегда имеет место даже при КЗ из режима холостого хода (ХХ). Это обусловлено влиянием активных сопротивлений роторных контуров. Действующий в Украине стандарт [2] предусматривает также определение электромагнитных параметров и частотных характеристик с учетом многоконтурности ротора.
Вопросы исследования математической модели, положенной в основу стандартной методики определения совокупности электромагнитных параметров СМ с учетом многоконтурности ротора по данным опытов ВКЗ в литературе не рассматривались.
Целью настоящей работы является уточнение математической модели ВКЗ СМ, позволяющей повысить точность определения электромагнитных параметров и частотных характеристик проводимости со стороны обмотки статора с учетом многоконтурности ротора.
Аналогичная задача для ЭМ с симметричным ротором рассматривалась в [9].
Анализ стандартного алгоритма. Математическая модель, принятая в [6, 7], представляет аналитическое выражение для фазных токов. При КЗ из режима холостого хода, например, для фазы А обмотки статора оно имеет вид:
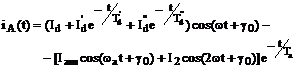 , (1)
, (1)
где ![]() - установившаяся, начальные значения
переходной, сверхпереходной, тока двойной частоты и максимально возможной
апериодической составляющих фазного тока;
- установившаяся, начальные значения
переходной, сверхпереходной, тока двойной частоты и максимально возможной
апериодической составляющих фазного тока; ![]() - постоянные времени затухания свободных
токов;
- постоянные времени затухания свободных
токов; ![]() - угол между
осью фазы А статора и осью d ротора в момент КЗ;
- угол между
осью фазы А статора и осью d ротора в момент КЗ; ![]() - частота вращения ротора;
- частота вращения ротора; ![]() - частота вращения апериодической
составляющей потока обмотки статора.
- частота вращения апериодической
составляющей потока обмотки статора.
Уравнение (1) представляет собой приближенное решение уравнений Парка-Горева при неучете активных сопротивлений обмоток статора и ротора на амплитуды и фазы соответствующих составляющих токов. Из анализа (1) следует, что токи ВКЗ отражают влияние только параметров СМ по продольной оси.
Выражение (1) при отказе от учета тока двойной частоты и вращения апериодического потока статора является математической моделью, которой соответствует алгоритм нахождения электромагнитных параметров, описанный пунктами 17 и 24 ГОСТ 10169-77 [2].
Выбор математической модели для определения электромагнитных параметров и частотных характеристик (ЧХ) с учетом многоконтурности ротора дан в [2]. В соответствии с пунктом 25.1 ГОСТ –10169-77 параметры машины по продольной оси следует определять по переходной функции, представляющей изменение огибающей периодического тока якоря из опыта ВКЗ. Эта составляющая определяется как полуразность ординат верхней и нижней огибающих фазного тока. Представляя периодическую составляющую тока суммой экспонент закон ее изменения во времени может быть описан функцией вида
![]() , (2)
, (2)
где ![]() - установившееся значение тока КЗ;
- установившееся значение тока КЗ; ![]() - начальное значение и постоянная
времени затухания k–ой экспоненциальной составляющей периодического тока; n
–количество экспонент, равное числу учитываемых контуров на роторе по продольной
оси.
- начальное значение и постоянная
времени затухания k–ой экспоненциальной составляющей периодического тока; n
–количество экспонент, равное числу учитываемых контуров на роторе по продольной
оси.
Переходной функции (2) соответствует следующее
выражение для определения ЧХ проводимости со стороны обмотки статора по
продольной оси ротора ![]()
![]() . (3)
. (3)
Параметры входящие в (3) определяются следующим образом:
![]() ;
; ![]() ;
; ![]() .
.
Соотношению (3) соответствует эквивалентная схема замещения с вынесенной на зажимы источника ветвью намагничивания, приведенная на рис. 1.
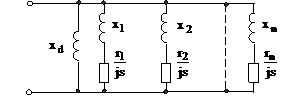
Рисунок 1 - Схема замещения ЭМ с вынесенной ветвью намагничивания
Таким образом с учетом многоконтурности ротора закон изменения фазного тока статора ВКЗ имеет вид, аналогичный (1), с той лишь разницей, что периодическая составляющая тока представляется не двумя, а тремя – четырьмя (по рекомендации [2]) экспонентами. Тогда можно предположить, что все рекомендации по уточнению стандартной методики нахождения электромагнитных параметров, предложенные в [6, 7], могут быть распространены и для определения частотных характеристик с учетом многоконтурности. Однако, необходимость представления переходного периодического тока тремя – четырьмя экспоненциальными составляющими, требует дополнительной оценки погрешности математической модели, соответствующей выражению (1).
Исследования проводились на примере расчета
токов при трехфазном КЗ на выводах модельного синхронного генератора типа МТ-30
(![]() ), имеющего
демпферную систему и обладающего существенно различными динамическими
свойствами по осям магнитной симметрии ротора. Параметры трехконтурных
эквивалентных схем замещения по каждой оси ротора указанного генератора
определялись методом затухания постоянного в обмотке статора неподвижной машины.
Кроме того исследования проводились также для явнополюсного синхронного
генератора типа СГ-18,75 без демпферной системы (
), имеющего
демпферную систему и обладающего существенно различными динамическими
свойствами по осям магнитной симметрии ротора. Параметры трехконтурных
эквивалентных схем замещения по каждой оси ротора указанного генератора
определялись методом затухания постоянного в обмотке статора неподвижной машины.
Кроме того исследования проводились также для явнополюсного синхронного
генератора типа СГ-18,75 без демпферной системы (![]() ).
).
На рис. 2 приведены результаты расчета тока статора при переходном процессе вызванном ВКЗ на выводах генератора МТ-30 при использовании различных математических моделей.

Рисунок 2 - Изменение тока статора при ВКЗ на выводах генератора МТ - 30
Сопоставление результатов моделирования, выполненного путем решения полных уравнений Парка-Горева (кривая 1) с расчетом по выражению (1) указывает на их несовпадение (кривая 2). Если в области максимальных мгновенных значений тока погрешность не превышает 6,2%, то в области минимальных - она достигает 44%. Использование выражения (1) при неучете составляющей двойной частоты дает качественно неверные результаты (кривая 3).
Анализ параметров многоконтурных эквивалентных схем замещения ряда турбогенераторов указывает на наличие роторных контуров, электромагнитные постоянные времени которых менее полупериода промышленной частоты. В этом случае рекомендация [6, 7], относительно нахождения электромагнитных параметров по периодическим составляющим тока каждой из фаз, делает невозможным выявление в составе переходных функций составляющих, имеющих постоянные времени менее 0,01 с. Это обусловлено тем, что измерение экстремальных мгновенных значений тока возможно с дискретностью не менее 0,01 с. Следует также отметить, что измерения только максимальных и минимальных значений вносит дополнительную погрешность вследствие того, они наступают со сдвигом в полпериода промышленной частоты.
Для повышение точности необходимо получение математической модели, основанной на описании закона изменения изображающего вектора тока статора. В этом случае регистрация переходных функций возможна с любой дискретизацией.
Уточненное определение переходного периодического тока статора СМ с помощью частотных характеристик. Получим уточненную модель на основе установленных в [8] и уточненных для АМ в [9] связях между частотными характеристиками, эквивалентными схемами замещения и составляющими переходного тока при коротких замыканиях.
Исследование переходных процессов с помощью частотных характеристик в СМ имеет свои особенности вследствие наличия асимметрии ротора. Это приводит к необходимости характеризовать машину двумя частотными характеристиками по продольной и поперечной осям магнитной симметрии ротора. Рассмотрим определение составляющих токов при КЗ на выводах СМ. Будем предполагать, что на роторе имеется несколько демпферных контуров и ротор имеет магнитную и электрическую несимметрию.
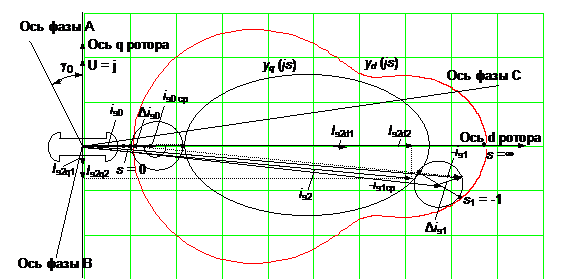
Рисунок 3 - Определение начальных значений переходных токов статора СМ при внезапном трехфазном КЗ
При КЗ в обмотке статора будут протекать: установившийся ![]() , апериодический -
, апериодический - ![]() и переходный периодический
-
и переходный периодический
- ![]() токи (рис.3).
токи (рис.3).
Математическая модель СМ представляет аналитическое выражение:
![]() . (4)
. (4)
В (4) отдельные составляющие переходного тока статора определяются по следующим соотношениям:
![]() , (5)
, (5)
![]() , (6)
, (6)
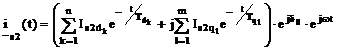 , (7)
, (7)
где ![]() - угол, характеризующий положение поперечной
оси ротора по отношению к вектору напряжения, подводимого к обмотке статора.
- угол, характеризующий положение поперечной
оси ротора по отношению к вектору напряжения, подводимого к обмотке статора.
При КЗ из режима холостого хода ![]() .
.
Для определения в (5) и (6) средних ![]() и пульсирующих
и пульсирующих ![]() составляющих токов используются
частотные характеристики
составляющих токов используются
частотные характеристики ![]() и
и ![]() соответственно. Эти характеристики отражают
магнитную и электрическую несимметрию ротора.
соответственно. Эти характеристики отражают
магнитную и электрическую несимметрию ротора.
![]() ,
, ![]() . (8)
. (8)
![]() ,
, ![]() . (9)
. (9)
Аналитическое представление ЧХ по (3)
позволяет непосредственно определять векторы отдельных составляющих ![]() и постоянные времени их затухания
и постоянные времени их затухания
![]() по параметрам
эквивалентных схем замещения.
по параметрам
эквивалентных схем замещения.
Составляющие переходного периодического тока
статора ![]() и
и ![]() при КЗ СМ будут
определяться как проекции на оси d и q соответствующих векторов, рассчитываемых
по следующим соотношениям:
при КЗ СМ будут
определяться как проекции на оси d и q соответствующих векторов, рассчитываемых
по следующим соотношениям:
![]() . (10)
. (10)
Поскольку в общем случае суммы найденных таким
образом амплитудных значений составляющих токов ![]() и
и ![]() не будут равны соответствующим амплитудам
векторов, найденным как проекции на оси d и q вектора полного периодического
тока статора
не будут равны соответствующим амплитудам
векторов, найденным как проекции на оси d и q вектора полного периодического
тока статора ![]() , то они
должны быть пересчитаны следующим образом:
, то они
должны быть пересчитаны следующим образом:
 ;
;
 (11)
(11)
На рис. 2 приведены результаты расчета по полученной математической модели (кривая 4).
Сопоставление с результатами расчета, выполненного путем решения полных уравнений Парка-Горева (кривая 1) свидетельствует об их практическом совпадении. Отличие в течение всего переходного процесса не превышает 1%. Аналогичные исследования, проведенные для синхронной машины СГ-18,75 показали практическое совпадение результатов расчета по уравнениям Парка-Горева, соотношению (1) и предложенной методике. Отличия не превышают 3%.
Это обусловлено тем, что вследствие малого
значения активного сопротивления ОВ вектор переходного периодического тока ![]() практически не имеет проекции
на поперечную ось q.
практически не имеет проекции
на поперечную ось q.
Вывод
Полученная в работе уточненная модель синхронной машины позволит повысить точность определения электромагнитных параметров с учетом многоконтурности ротора по данным обработки переходных функций токов статора при внезапном трехфазном коротком замыкании.
Список литературы
1. International Electrotechnical Commission (IEC) Standard. Rotating Electrical Machines. Part 4: Methods for determining synchronous machines quantities from tests. Publication 34-4. Geneva, 1985.- 175 p.
2. ГОСТ 10169-77. Машины электрические синхронные трехфазные. Методы испытаний. – М.: Изд-во стандартов, 1984. – 78 с.
3. Kamwa I., Viarouge P., Machfoudi R. Phenomenological models of large synchronous machine from short-circuit test during comissioning - A clasical / modern approach // IEEE Tranc. on Energy Conversion. 1994. V.9. № 1.P. 85-97.
4. Kamwa I., Viarouge P., Pilote M., et al. Computer software to automatic graphical analysis of sudden - short - circuit oscillograms of large synchronous machines // IEEE Tranc. on Energy Conversion. 1995. V.10. № 3.P. 399-406.
5. Kamwa I., Viarouge P., Experience with computer -aided graphical analysis of sudden - short - circuit oscillograms of large synchronous machines // IEEE Tranc. on Energy Conversion. 1995. V.10. № 3.P. 407-414.
6. Харченко В.А. О разбросе значений параметров синхронных машин, находимых из опыта внезапного короткого замыкания // Изв. РАН. Энергетика. – 1996. - № 2. – С. 127 – 137.
7. Харченко В.А. Еще раз о разбросе значений параметров синхронных машин, находимых из опыта внезапного короткого замыкания // Изв. РАН. Энергетика. – 1999. - № 1. – С. 142 – 151.
8. Казовский Е.Я. Переходные процессы в электрических машинах переменного тока. - М.: Изд-во АН СССР, 1962.-624 с.
9. Ларин А.М., Ламари Абдессалеи, Ларина И.И. Экспериментальное определение частотных характеристик асинхронных машин при различных уровнях насыщения // Електротехніка і Електромеханіка.– 2003.- №4. – С.52-58.