Абдессалем ЛАМАРИ

Источник:Електротехніка і електроніка. – 2009. – №7. – стор. 40 – 45.

1. ВВЕДЕНИЕ

Распространение в инженерной практике исследования динамических режимов электрических машин переменного тока (ЭМ) при коротких замыканиях в электрических системах получили частотные методы [1,5,6]. Они позволяют непосредственно использовать для расчета экспериментальные данные в виде частотных характеристик отдельных элементов или всей системы в целом, не вникая в структуру их внутренних взаимосвязей. В условиях, когда внутренняя структура не определена, такой подход к расчету переходных процессов может дать более точные результаты.

В [1] предложен метод расчета переходных процессов по частотным характеристикам проводимостей синхронной машины (СМ)  и  или токовым диаграммам асинхронных (АМ) машин. При этом разработаны графо-аналитические способы расчета токов статора и электромагнитного момента. Они позволяют проводить уточненные расчеты переходных процессов с учетом таких факторов, как электромагнитная асимметрия ротора, многоконтурность массивных роторов турбогенераторов, вытеснение тока в обмотках электрических машин, насыщение магнитных цепей, наличие дополнительных сопротивлений в обмотке статора. Однако, указанные способы не получили в свое время широкого распространения.

Широкое внедрение ПЭВМ, накопление информации о синхронных и асинхронных машинах в форме частотных характеристик, а также развитие методов синтеза эквивалентных схем замещения, адекватно описывающих исходные частотные характеристики, создают предпосылки для усовершенствования и дальнейшего развития частотных методов исследования динамических режимов ЭМ.

Целью настоящей работы является разработка математических моделей ЭМ на основе экспериментальных статических частотных характеристиках для исследования переходных процессов при коротких замыканиях и включениях машин в сеть с учетом изменения скорости вращения.

2. МАТЕМАТИЧЕСКИЕ СООТНОШЕНИЯ

В [2] получены математические соотношения, реализующие графо-аналитический подход [1] к определению составляющих фазных токов статора и электромагнитного момента вращения при коротких замыканиях (КЗ) или включениях синхронных генераторов в сеть, вращающихся с синхронной скоростью. При наличии скольжения в момент подключения ЭМ с асимметричным ротором к сети или при КЗ расчет для отдельных составляющих изображающего вектора тока статора  ведется в следующей последовательности:

Определяется среднее значение установившегося тока  для скольжения s в момент включения машины

,(1)

где

.

Рассчитывается пульсирующая составляющая установившегося тока

,(2)

где ;   - угол между поперечной осью ротора и вектором напряжения сети.

Рисунок 1 - Схема замещения синхронной машины по продольной оси ротора

Находится изменение во времени полного установившегося тока статора с учетом различия параметров ротора по осям магнитной и электрической симметрии:

.(3)

Определяется апериодическая составляющая

 (4)

и периодический ток частоты близкой к двойной:

.(5)

Изменение во времени апериодического тока и тока, обусловленного асимметрией ротора, подчинено следующему закону

 (6)

Собственная частота вращения апериодического тока () и постоянная времени его затухания определяются по значению среднего комплекса проводимости  для скольжения .

, (7)

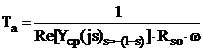. (8)

Начальное значение переходного периодического тока  рассчитывается из условия

.

В общем случае, начальное значение вектора тока  не совпадает с продольной осью ротора (даже при включениях с углом ), что соответствует возникновению апериодических токов в контурах ротора по обеим осям его магнитной симметрии.

Необходимым условием для реализации предложенного способа является аналитическое описание исходных частотных характеристик и закона изменения во времени переходной периодической составляющей тока статора. В [3] предложена методика использования для этих целей эквивалентных схем замещения, представленных на рис. 1.

Указанные схемы замещения позволяют определять начальные значения и постоянные времени () экспоненциальных составляющих тока . Для продольной оси, например, имеем:

,

.(9)

Следовательно, закон изменения периодического затухающего тока во времени будет таким

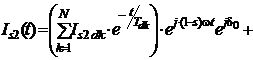
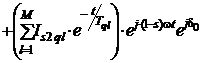    ,   (10)

где N - количество контуров на роторе по продольной оси; M – то же по поперечной оси.

В общем случае начальные значения продольных и поперечных составляющих тока  должны пересчитываться пропорционально проекциям полного вектора указанного тока на продольную  и поперечную оси ротора.

,

,  (11)

где -аргумент вектора тока  (угол между вектором тока и осью действительных чисел комплексной плоскости. Тогда:

,

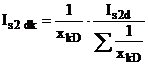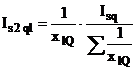. (12)

Полный вектор изображающего тока статора представляет собой векторную сумму отдельных составляющих:

, (13)

где U - напряжение на выводах статора при коротком замыкании или включении ЭМ в сеть.

Мгновенные значения фазных токов определяются как проекции изображающего вектора на неподвижные оси времени соответствующих фаз:

,

,

, (14)

где  - аргумент полного изображающего вектора тока статора, зависящий от времени.

Для описания динамических свойств асинхронной машины достаточно иметь одну частотную характеристику . В этом случае в полученных соотношениях будут отсутствовать составляющие токов  и . Отпадает также необходимость в разложении на составляющие по осям магнитной симметрии тока .

Электромагнитный момент в соответствии с общим подходом к его определению по значениям комплексов токов и потокосцеплений будет определяться для ЭМ с симметричным или асимметричным ротором следующим выражением:

. (15)

Потокосцепления в (15) имеют следующие значения:

.(16)

Рассматривая комплексы как векторы, электромагнитный вращающий момент можно представить как сумму векторных произведений составляющих тока на составляющие потокосцеплений. Произведение, например,  на  даст установившийся вращающий момент, численно равный величине вертикальной проекции вектора тока  при номинальном напряжении на выводах статора. Проанализировав влияние отдельных составляющих токов и моментов на характер протекания переходного процесса, можно осуществить упрощение математической модели с заданной точностью.

При исследовании электромеханических переходных процессов, связанных с изменением скорости вращения машины совместно с полученными выше уравнениями, описывающими изменение электрических величин, необходимо рассматривать уравнение движения ротора. Последнее может быть записано в следующем виде

,(17)

где Ммех – внешний механический момент, приложенный к ротору;  Tj – механическая постоянная инерции.

3. АЛГОРИТМ РАСЧЕТА

При неучете влияния ускорения может быть предложен следующий алгоритм расчета переходных процессов с учетом изменения скорости вращения ротора.

- Весь процесс разбивают на ряд равномерных интервалов по времени.

- На каждом интервале в соответствии с (17) находят изменение скольжения

.

- Установившуюся составляющую тока  рассчитывают как при постоянной скорости, подставляя для каждого момента времени действительную скорость вращения ротора в качестве переменного параметра.

- Амплитуду составляющей , затухающей с постоянной времени , рассчитывают для значения скорости в начальный момент времени.

- Собственную частоту вращения  и постоянную  пересчитывают по выражениям (7) и (8) в зависимости от изменения скольжения.

- Амплитуду составляющей тока , обусловленной переходными токами в роторных контурах, определяют для значения скольжения в начальный момент времени.

- Скорость вращения тока , учитываемая в (9), изменяется при изменении скольжения.

- Учитывается зависимость от скольжения собственной частоты вращения и постоянной времени затухания потокосцепления  в (16).

4. ОЦЕНКА ДОСТОВЕРНОСТИ МОДЕЛЕЙ

Эффективность применения частотных характеристик к анализу динамических режимов исследовалась на примере расчетов следующих переходных процессов:

1. Короткое замыкание на выводах и включение в сеть невозбужденного модельного турбогенератора типа МТ-30. Указанный генератор обладает существенно различными динамическими свойствами по осям магнитной симметрии ротора и имеет следующие параметры:

При этом анализировалось влияние величины и знака скольжения в момент подключения СМ к сети, а также влияние изменения скорости вращения ротора в переходных режимах.

2. Для турбогенератора типа ТГВ-200 оценивалась погрешность, вносимая в расчет электромеханических переходных процессов, за счет эквивалентирования многоконтурных схем замещения, отображающих электромагнитную асимметрию ротора.

3. Для асинхронного электродвигателя типа ДАЗО-1914-10/12А (Рном = 1500 кВт; Iном = 204 А; Uном = 6000 В) были выполнены расчеты электромеханических переходных процессов при пуске из ненагруженного состояния и электромагнитных – при трехфазном КЗ на его выводах.

Оценка степени достоверности результатов расчетов по предлагаемой в работе методике осуществлялась путем сравнения с соответствующими результатами расчетов, выполненными по алгоритмам, реализующим численное интегрирование полных дифференциальных уравнений Парка-Горева. Частотные характеристики для исследуемых ЭМ определялись по методу затухания постоянного тока в обмотках статора [5].

Программы, реализующие алгоритмы расчета электромеханических переходных процессов, была разработаны  в среде математической системы MathCAD 7.0.

Расчеты зависимости изменения изображающего тока статора и электромагнитного момента вращения при включении невозбужденного модельного генератора МТ-30 в сеть для различных начальных скольжений ротора выполнялись без учета и с учетом изменения скорости вращения ротора после подключения СГ к сети. Постоянство скорости вращения моделировалось путем задания механической постоянной инерции  большой величиной. Как следует из сопоставления результатов расчета, выполненных для скольжений 0; 0,01; 0,03; 0,05 и 0,1о.е., изменение зависимостей изображающего тока статора и электромагнитного момента практически совпали с соответствующими расчетами, выполненными по уравнениям Парка-Горева при постоянном скольжении. При этом отличия в максимальных значениях сопоставляемых параметров не превышает 10,4%. Характер процессов оказался абсолютно идентичным. Это позволяет утверждать, что электромагнитные процессы, отображаются при использовании статических частотных характеристик достаточно точно.

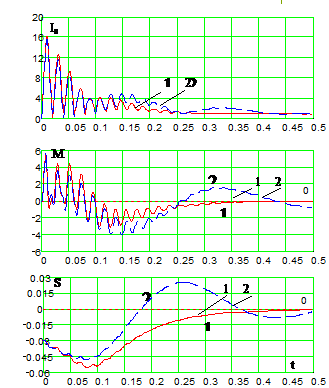
Рисунок 2 - Включение в сеть невозбужденного генератора типа МТ - 30

Рисунок 3 - КЗ на выводах АД ДАЗО - 1914 - 10/12А

Анализ результатов расчета с учетом изменения скорости вращения ротора после включения СГ в сеть указывает на некоторые отличия в зависимостях изменения параметров динамического режима. На рис.2, в качестве примера, приведены результаты расчета переходных процессов при включении в сеть невозбужденного модельного синхронного генератора типа МТ-30 при короткозамкнутом состоянии обмотки возбуждения.

В расчетах, выполненных по уравнениям Парка-Горева (кривые 2), отражается динамика процесса, связанная с изменением токов (Is) и электромагнитных моментов (M) при изменении скорости вращения. Изменение скольжения (S) при этом носит колебательный характер. Моделирование, использующее статические характеристики (кривые 1), приводит к монотонному изменению скольжения ротора в переходном режиме. Однако, общее время приближения скорости к синхронной, оцениваемое по времени второго прохождения скольжения через ноль, практически совпало со временем достижения ротором синхронной скорости, полученное при моделировании по предложенной методике. В целом характер изменения исследуемых параметров режима совпал. Максимальные их значения, возникающие в начальной стадии переходного процесса, практически не отличаются от данных, полученных без учета изменения скорости.

На рис.3 приведены кривые изменения параметров режима при коротком замыкании на выводах асинхронного двигателя типа ДАЗО–1914–10/12А.

Параметры трехконтурной схемы замещения с вынесенной ветвью намагничивания, аналогичной показанной на рис.1., синтезированные по [4], имеют следующие значения (о.е.):

; ; ; ;; ; .

Сопоставительный анализ результатов расчета изображающего тока статора (Is) и электромагнитного момента (М), выполненных различными методами свидетельствует об их удовлетворительном совпадении: погрешность в максимальных значениях указанных параметров не превысила 7,8%.

Исследование электромеханических переходных процессов при пуске ненагруженного асинхронного двигателя, также указывает на удовлетворительное совпадение результатов расчета, выполненных различными способами (с точки зрения длительности процесса пуска). Время пуска, определенное по предложенной методике, отличается от рассчитанного по полным уравнениям Парка-Горева, на 9,2%.

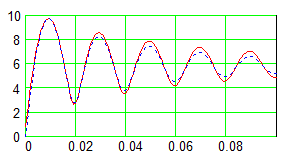
Рисунок 4 - Изменение изображения тока при включении в сеть АД типа ДАЗО - 1914

Переходные процессы в течение времени, определяемым протеканием электромагнитных явлений, оказались близкими по характеру и значениям. В области времен от 0 с до 1,8 с. параметры исследуемого режима практически совпадают между собою (рис.4).

 Это объясняется тем, что изменение скорости вращения ротора происходит с малым ускорением и использование статических характеристик практически не вносит погрешность в динамический процесс. В области времен, когда скорость вращения ротора близка к номинальной, в характере изменения тока статора и электромагнитного момента имеются существенные отличия. Исследования показали, что эти отличия уменьшаются при увеличении  и коэффициента загрузки двигателя, поскольку в этом случае процессы сопровождаются меньшими ускорениями ротора.

Исследования, выполненные при анализе переходных процессов, вызванных включением невозбужденного турбогенератора типа ТГВ-200 в сеть, для пятиконтурных и трехконтурных эквивалентных схем замещения [3], показали, что погрешности, вносимые сокращением количества контуров в изменения параметров режима во временной области, не превышают погрешностей, в частотной области, и составляют 7-11%.

5. ВЫВОД

1. Предложенные математические модели электрических машин переменного тока, основанные на экспериментальных статических частотных характеристиках, позволяют без решения дифференциальных уравнений исследовать динамические переходные режимы при коротких замыканиях и включениях ЭМ в сеть.

6. БИБЛИОГРАФИЯ

1. Казовский Е.Я. Переходные процессы в электрических машинах переменного тока. - М.: Изд-во АН СССР, 1962.-624 с.

2. Ларин А.М., Ларина И.И., Гуедиди Фаузи. Упрощенная модель синхронной машины для расчета трехфазных коротких замыканий с учетом многоконтурности и несимметрии ротора. Научные труды ДонГТУ, серия Электротехника и энергетика, вып.4. Донецк, 1999. – С. 60-64.

3. Ларин А.М., Ламари Абдессалем. Определение параметров схем замещения турбогенераторов, отображающих электромагнитную несимметрию их массивных роторов. Научные труды ДонГТУ, серия: Электротехника и энергетика, вып.4. Донецк, 1999. – С. 65-68.

4. Рогозин Г.Г., Ларин А.М. Расчет параметров эквивалентных роторных контуров синхронных машин по их экспериментальным частотным характеристикам / Электричество, 1974,  № 6.  С.10 - 13.

5. Рогозин Г.Г. Определение электромагнитных параметров машин переменного  тока. – К.: Техніка, 1992. – 168 с.  

6. Применение частотных методов в электроэнергетическом исследовании. Труды СибНИИЭ / Под ред Лукашова Э.С. – Новосибирск, 1972, вып. 21. – 294 с