где Tr = Lr / Rr; kr = Lm / Lr.
Виноградов А.Б. Векторное управление электроприводами переменного тока / ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина». — Иваново, 2008. — 298 с., с. 187-195.
Развитие векторных систем пошло по пути перехода от непосредственного измерения потока к определению его значения с помощью математической модели электромагнитных процессов в асинхронном двигателе (модели потока). Такое направление развития векторных систем стало возможным в результате успехов в области силовой электроники и микропроцессорной техники.
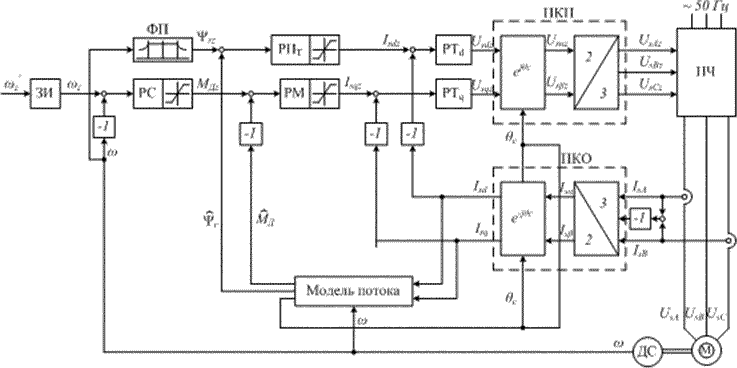
Функциональная схема системы регулирования скорости электропривода при векторном управлении асинхронным двигателем и определении потокосцепления ротора по модели потока приведена на рис.11.7,а. Питание двигателя осуществляется от преобразователя частоты со звеном постоянного тока и инвертором, управляемым током. В показанном на рис.11.7,а варианте схемы быстродействующие токовые контуры выполнены во вращающейся системе координат. Поэтому контуры регулирования токов по прямой Isd и квадратурной Isq осям включают в себя преобразователи координат прямого и обратного каналов (ПКП и ПКО). На входах регуляторов токов и сравниваются между собой сигналы задания токов Isdz и Isqz и истинные значения соответствующих токов. Выходные сигналы регуляторов тока Usdz и Usqz являются сигналами задания напряжения инвертора. Во вращающейся системе координат напряжения на выходе инвертора UsA, UsB и UsC создают токи в статорных обмотках двигателя IsA, IsB и IsC, которые после преобразования их в ПКО во вращающуюся систему координат служат сигналами обратных связей по току.
Модель потока показана на рис.11.7,б. Получаемые в модели значения потокосцепления ротора и частоты роторной ЭДС записываются в виде


где Tr = Lr / Rr; kr = Lm / Lr.
Первое из этих выражений показывает, что при ориентации вещественной оси вращающейся системы координат по вектору потокосцепления ротора значение потокосцепления однозначно определяется составляющей тока статора по прямой оси d. Второе – дает возможность при известном значении потокосцепления рассчитать значение частоты роторной ЭДС по составляющей тока статора по квадратурной оси q. Расчет потокосцепления ротора и частоты роторной ЭДС по приведенным формулам обеспечивает ориентацию оси d по вектору Ψr.
Кроме модуля потокосцепления ротора и роторной частоты в модели потока рассчитывается текущее значение угла поворота θc с вращающейся системы координат (d, q) относительно связанной со статором неподвижной системы координат (α, β), а также значение электромагнитного момента двигателя MД. Сумма измеренного значения скорости, умноженного на число пар полюсов и рассчитанного в модели значения роторной частоты, определяет текущее значение частоты напряжения на статоре

Интегрирование этой величины в интеграторе дает текущее значение угла θc. Это значение используется в блоках ejθc и e-jθc преобразователей координат прямого канала и канала обратной связи для расчета необходимых значений sin θc и cos θc.
 а)
а) б)
б)При ориентации оси d по вектору Ψr и расчете через амплитудное значение потокосцепления ротора и проекцию вектора тока статора на квадратурную ось электромагнитный момент рассчитывается по выражению

Если бы Ψr и Isq представляли собой проекции пространственных векторов, модули которых приняты равными эффективным (действующим) значениям величин, то для определения момента нужно было бы воспользоваться формулой
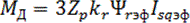
Система управления электроприводом выполнена во вращающейся системе координат и построена по принципам подчиненного регулирования. Внешним по отношению к контуру тока по оси d является контур регулирования потокосцепления ротора с регулятором потока РПт. Выходной сигнал регулятора потока представляет собой сигнал задания составляющей тока статора по вещественной оси Isdz. На входе регулятора сравниваются сигнал задания Ψrz и истинное значение потокосцепления ротора Ψr, определенное в модели потока. Внешним по отношению к контуру регулирования тока Isq является контур регулирования момента со своим регулятором РМ. На его входе сравниваются выходной сигнал регулятора скорости MДz, который задает значение электромагнитного момента, и сигнал обратной связи по моменту MД, вычисленный в модели. Контур регулирования скорости с регулятором РС замкнут по сигналу с выхода датчика скорости ДС.
В рассматриваемой схеме исключение влияния перекрестных связей, имеющихся в математической модели двигателя, обеспечивается путем использования быстродействующих контуров регулирования токов. Это позволяет рассматривать подсистему регулирования потокосцепления ротора как не связанную с подсистемой регулирования момента и делает возможным независимое регулирование потокосцепления ротора подобно тому, как происходит регулирование потока возбуждения в двигателе постоянного тока с независимым возбуждением. В частности, существует возможность предварительного намагничивания двигателя, т. е. возможность установить поток до того, как на контур скорости будет подан сигнал задания скорости и когда скорость двигателя равна нулю.
Если требуется двухзонное регулирование скорости, то в системе предусматривается функциональный преобразователь (ФП). Входной сигнал на нем определяется значением скорости. До тех пор пока скорость не превышает номинальное значение, сигнал на выходе ФП задает номинальный поток и остается постоянным. Когда скорость превысит номинальное значение, сигнал на выходе ФП будет уменьшаться и скорость, большая номинальной, будет достигнута при ослаблении потокосцепления ротора и значении напряжения на статоре, близком к постоянному.
На входе системы предусмотрен задатчик интенсивности (ЗИ). При подаче на его вход сигнала задания скорости любой, например ступенчатой, формы изменение сигнала задания скорости на выходе задатчика происходит по линейному или другому заданному закону, что обеспечивает плавный характер разгона и торможения привода.
В соответствии с принципом подчиненного регулирования для ограничения выходной величины внутреннего («подчиненного») контура надо ограничить выходной сигнал регулятора внешнего по отношению к нему контура. Поэтому для ограничения токов статора по прямой и квадратурной осям предельно допустимыми значениями, в регуляторах потока РПт и момента РМ предусмотрены блоки ограничения выходных сигналов Isdz и Isqz. Аналогичный блок для ограничения момента двигателя предусмотрен в регуляторе скорости.
Ограничение выходного сигнала регулятора внешнего контура вступает в действие, если в переходном процессе сигнал ошибки на его входе, представляющий собой разность между сигналом задания и сигналом обратной связи, станет недопустимо большим. При наличии блока ограничения выходная величина регулятора внешнего контура фиксируется на предельном значении до тех пор, пока ошибка на его входе не снизится до допустимого значения. Наличие блока ограничения не только на регуляторе момента, но и на регуляторе скорости позволяет независимо ограничивать значения момента двигателя и тока статора по оси q.
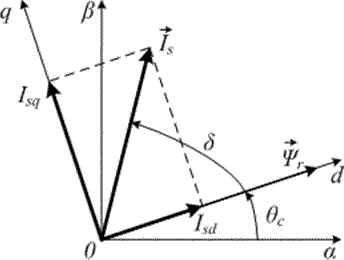
При выборе значений ограничения токов Isd и Isq надо иметь в виду, что они должны быть выбраны так, чтобы модуль полного тока статора, определяемый как
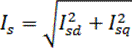
не превышал предельно допустимого значения Isогр. Это поясняется пространственной векторной диаграммой рис.11.8,а, на которой показаны пространственный вектор тока статора Is и токи статора по прямой и квадратурной осям.
На рис.11.8,б приведена структура блока ограничения тока, обеспечивающего ограничение сигналов задания токов статора по прямой и квадратурной осям таким образом, что полный ток ограничивается на уровне Isогр, независимо от соотношения между токами Isd и Isq. На входе схемы действуют выходные величины регуляторов РПт и РМ, которые в этом случае не содержат блоков ограничения. Эти величины обозначены как I'sdz и I'sqz. После возведения их в квадрат в блоке √ рассчитываются текущее значение модуля сигнала задания тока статора

и тригонометрические функции угла между текущим положением вектора тока статора и осью d вращающейся системы координат.

Сигнал на выходе звена ограничения модуля тока обозначен как Isz. Сигналы на выходах блока ограничения Isdz и Isqz являются сигналами задания для контуров регулирования тока.
Если |I'sz| ≤ Isогр, в результате чего Isdz = |I'sdz| и Isqz = |I'sqz|, т. е. блок ограничения не оказывает влияния на работу схемы. Если |I'sz| > Isогр, то Isz = I'sz и выполняются следующие равенства:


С учётом этих выражений модуль сигнала задания тока статора, определённый как корень квадратный из суммы квадратов токов Isdz и Isqz, будет равен
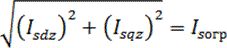
т.е. независимо от соотношения сигналов на выходах регуляторов потока и момента модуль полного тока всегда будет ограничен на уровне Isогр.
В приводе с асинхронным двигателем режим предварительного намагничивания обеспечивается заданием прямой составляющей тока статора, формирующей потокосцепление ротора, раньше, чем будет задана квадратурная составляющая, формирующая момент. В рассматриваемом блоке при подаче сигнала задания Ψrz на вход контура регулирования потокосцепления ротора величина Isdz ограничивается значением Isогр, обеспечивая форсированное нарастание потокосцепления. В то же время при раздельном ограничении токов Isd и Isq (см. рис.11.7,а) величина Isdz ограничивается значением меньшим, чем Isогр, т. е. поток нарастает медленнее.
При рассмотрении принципа построения системы (см. рис.11.7) предполагалось, что параметры двигателя стабильны во времени, а параметры модели потока точно соответствуют параметрам двигателя и остаются неизменными. В действительности параметры двигателя могут изменяться в зависимости от внешних причин. Например, активное сопротивление обмоток статора и ротора зависит от температуры, которая зависит от тока, протекающего по ним, и от температуры окружающей среды. Кроме того, магнитную систему двигателя не всегда можно рассматривать как ненасыщенную, характеризуемую постоянными значениями индуктивностей. Расхождения между изменившимися реальными параметрами двигателя и неизменными параметрами модели приводят к отклонению процессов в приводе от расчетных, не позволяя в полной мере использовать достоинства векторного управления. Поэтому необходима подстройка модели к нестабильным параметрам двигателя. Это одна из важных задач, возникающих при разработке системы. Существует ряд методов ее решения. Остановимся на двух сравнительно простых задачах параметрической адаптации, позволяющих учитывать в модели потока изменение сопротивления из-за нагрева обмоток и насыщение магнитной системы машины.
Для решения первой задачи в двигателе предусматривается автоматический контроль температуры обмоток с помощью датчиков температуры. В зависимости от нее сопротивления обмоток рассчитываются системой управления на основании специальной тепловой модели двигателя. По полученным значениям в реальном времени корректируется модель.
На основании выражения для постоянной времени ротора Tr = Lr / Rr в ненасыщенной машине уравнения роторной цепи можно записать в виде
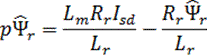
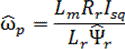
Главная индуктивность Lm, входящая в эти выражения непосредственно или как составная часть полной индуктивности ротора Lr = Lm + Lrσ, входит во все слагаемые, стоящие в правых частях. Следовательно, если учитывать изменение индуктивности за счет насыщения, то надо вносить изменения в три члена этих равенств. Задачу можно упростить.
Будем под Lm по-прежнему понимать главную индуктивность ненасыщенной машины, а индуктивность насыщенной машины обозначим через L'm. Связь между значениями этих индуктивностей определим следующим образом:
L'm = λLm
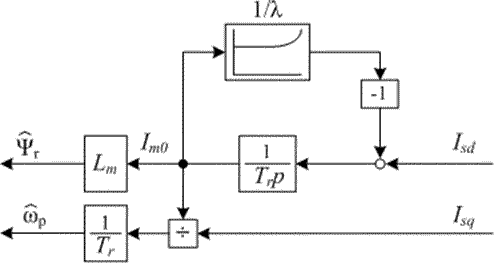
где λ — нелинейный коэффициент, значение которого может быть определено по известной характеристике L'm = f(|Im|) с учётом того, что в ненасыщенной части характеристики выполняется равенство L'm = Lm. Введем величину Im0 как ток, который соответствовал бы данному значению потокосцепления ротора, если бы характеристика была линейной:
Im0 = Ψr / Lm,
откуда можно выразить потокосцепление ротора в виде
Ψr = LmIm0. (11.7)
Считая так же, что индуктивность рассеяния не зависит от насыщения, можно полную индуктивность ротора в насыщенной машине записать в виде L'r = L'm + Lrσ. Тогда вместо первого из равенств (11.6) можно записать
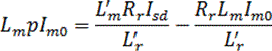
Имея в виду, что L'm >> Lrσ, можно с определенной погрешностью принять, что L'r = L'm + Lrσ = λLm + Lrσ ≈ λLr. С учетом этого последнее равенство приобретет вид
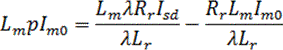
После введения обозначения Tr = Lr / Rr и сокращения на Lm получим математическое описание части модели, в которой потокосцепление ротора определяется по выражению (11.7):

Путём аналогичных преобразований может быть получено выражение для рассчитываемой в модели частоты роторной ЭДС:

Структурная схема рассматриваемой модели потока, построенная по этим формулам с учётом равенства (11.7), показана на рис.11.9. Для учёта нелинейности характеристики намагничивания только потребовалось ввести в модель нелинейный блок 1 / λ.