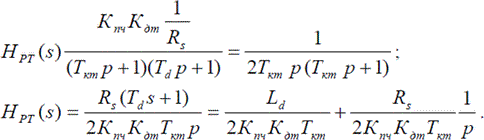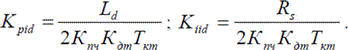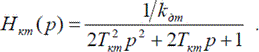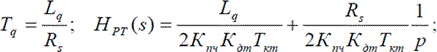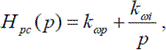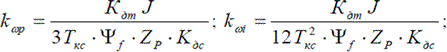Виноградов А.Б. Векторное управление электроприводами переменного тока / ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина». — Иваново, 2008. — 298 с., с. 252-256.
14.1. Пример построения системы векторного управления синхронным двигателем с постоянными магнитами
Рассмотрим построение системы векторного управления синхронным двигателем с постоянными магнитами (СДПМ).
Область применения таких систем: высококачественный электропривод подач металлорежущих станков. Основные характеристики контура регулирования скорости: диапазон регулирования — не менее 10000, полоса пропускания — не менее 100 Гц.
Синтез системы управление выполним на основе динамической модели СДПМ в системе координат (d,q), ориентированной по магнитной оси ротора [39]:
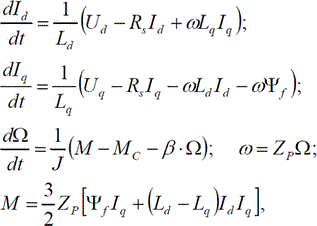
где Id, Iq, Ud, Uq — токи и напряжения статора по осям d и q; М, Мc — электромагнитный и нагрузочный моменты; ω — частота вращения ротора, электрическая; J — момент инерции ротора; β — коэффициент вязкого трения (коэффициент демпфирования); Ψf — потокосцепление, создаваемое постоянным магнитом; Ld, Lq — индуктивности обмотки статора по продольной поперечной осям ротора.
Для частного случая неявнополюсной конструкции ротора двигателя Ld = Lq = Ls.
Функциональная схема системы векторного управления СДПМ изображена на рис.14.1.
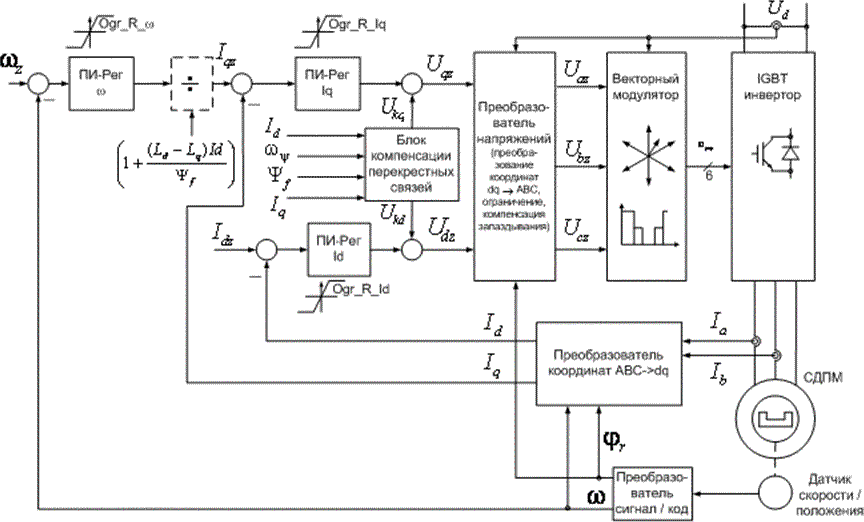
Рис. 14.1. Функциональная схема системы векторного управления СДПМ
Нулевое задание тока по оси d обеспечивает минимизацию тока статора при заданной величине момента нагрузки. В этом случае ток статора во всех режимах работы привода направлен перпендикулярно магнитной оси ротора (по оси q).
Преобразователь координат ABC → dq выполняет преобразование фазных токов статора АД из естественной трехфазной системы координат (А,В,С) в ортогональную синхронную систему координат (d,q) по уравнениям
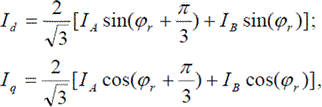
где φr — угловое положение ротора (электрическое), полученное с датчика положения.
Алгоритмы работы преобразователя напряжений и векторного модулятора аналогичны рассмотренным в разд. 11.4 для векторной системы управления асинхронным двигателем.
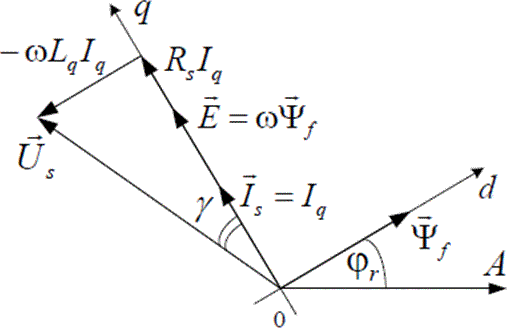
Рис. 14.2. Векторная диаграмма СДПМ
Блок компенсации перекрестных связей работает по следующим уравнениям:
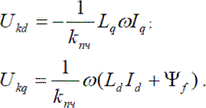
Синтез регуляторов осуществим на основе принципов подчиненного регулирования с использованием метода компенсации нелинейных связей.
Выполним синтез регулятора тока по оси d.
Структурная схема контура тока по оси d изображена на рис.14.3.
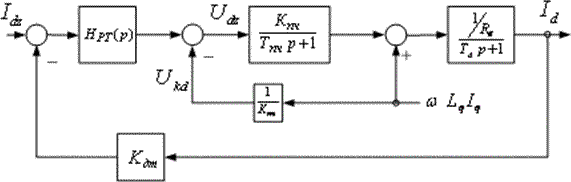
Рис. 14.3. Структурная схема контура тока по оси d
Обозначения: 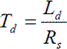 — постоянная времени статорной цепи по оси d;
— постоянная времени статорной цепи по оси d;
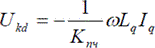 — сигнал компенсации влияния нелинейной перекрёстной связи.
— сигнал компенсации влияния нелинейной перекрёстной связи.
Считая влияние перекрестной связи полностью скомпенсированным, выполним настройку контура на модульный оптимум с малой некомпенсируемой постоянной времени Tкт = Tпч. В результате получим:
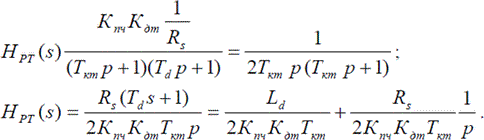
Таким образом, коэффициенты пропорциональной и интегральной составляющих ПИ регулятора тока по оси d определяются выражениями
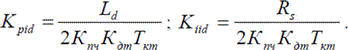
Передаточная функция замкнутого контура тока
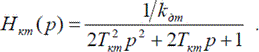
Синтез регулятора тока по оси q выполняется аналогично, с учетом следующих условий:
1) 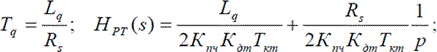
2) Сигнал возмущающей перекрестной связи, подлежащей компенсации, имеет вид
Ukq = ω(LdId + Ψf).
Выполним синтез регулятора скорости.
Структурная схема контура скорости для общего случая изображена на рис.14.4.
Второй (реактивной) составляющей момента (см. последнее уравнение системы (14.1)) можно пренебречь в следующих случаях:
1) для неявнополюсных машин (Ld = Lq);
2) при управлении по закону Id = 0 для любых типов СДПМ.
В этих случаях,
M=3/2ZpΨfIq (14.4)
где Ψf = const.
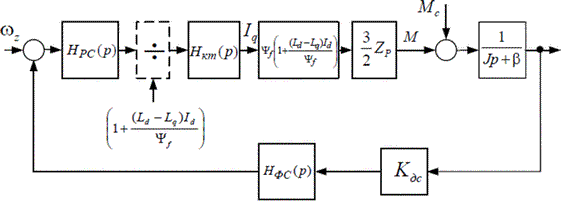
Рис.14.4. Структурная схема контура скорости
Для частного случая β = 0 настройка контура скорости выполняется на симметричный оптимум. В результате получается ПИ-регулятор скорости с передаточной функцией
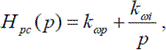
где 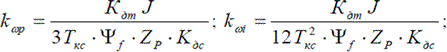
Tкс = 2Tкт + Tфс, Tфс — постоянная времени фильтра скорости.
Для общего случая β ≠ 0 настройка контура скорости выполняется на модульный оптимум.
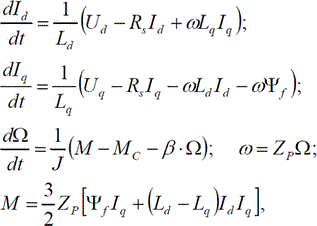

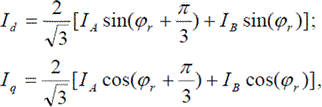

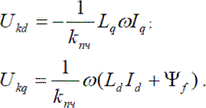

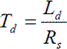 — постоянная времени статорной цепи по оси d;
— постоянная времени статорной цепи по оси d;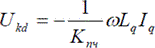 — сигнал компенсации влияния нелинейной перекрёстной связи.
— сигнал компенсации влияния нелинейной перекрёстной связи.