Источник:http://www.nbuv.gov.ua/portal/natural/emeo/ee_55/14.html
Постоянное увеличение числа и единичной мощности электрических двигателей привело к необходимости более детального анализа переходных процессов происходящих в двигателях, их влияния на режим системы электроснабжения, а также взаимного влияния электродвигателей.
Следует отметить, что при моделировании переходных процессов в многомашинных системах, если и выполняется учет электромагнитных переходных процессов, то делаются всяческие попытки уйти от записи уравнения равновесия напряжений для внешней сети в дифференциальной форме 
, т.е. для внешней сети пользуются уравнением установившегося режима. Это связано, в первую очередь, с тем, что для моделирования многомашинных систем с применением дифференцирования для отражения процессов в сети необходима высокопроизводительная вычислительная техника, ресурсы которой до последнего времени были ограничены.
На современном этапе развития, вычислительная техника обладает достаточными ресурсами. В связи с этим особую актуальность приобретает создание моделей многомашинных систем для промышленных предприятий, в которых учитываются быстропротекающие электромагнитные процессы и применяются дифференциальние уравнения для внешней сети.
При необходимости подробного анализа переходных процессов в многомашинных системах электроснабжения промышленных предприятий с расчетом мгновенных значений режимных параметров и выяснения взаимного влияния двигателей друг на друга, обязательна запись уравнения равновесия напряжений для внешней сети в дифференциальной форме. Для электрических двигателей также обязательно использование «полных» систем уравнений, например, моделирование синхронных двигателей (СД) по полным уравнениям Парка-Горева (уравнения для цепей статора, ротора и уравнение движения). Все это позволит учесть как электромагнитные так и электромеханические переходные процессы.
Несмотря на все многообразие схем электроснабжения в большинстве случаев все они могут быть приведены к виду, более удобному для моделирования. На рис. 1 приведен общий вид простейшей расчетной схемы многомашинной системы.
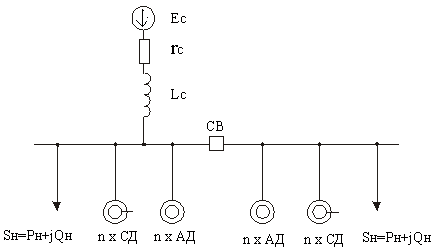
На рисунке ЕC, rC, LC — соответственно эквивалентные ЭДС, активное сопротивление и индуктивность системы. В эквивалентные активное сопротивление и индуктивность системы в общем случае входят сопротивления внешней системы электроснабжения и трансформатора главной понижающей подстанции предприятия.
При моделировании многомашинных систем очень важно установить в каких системах координат следует записать уравнения электрического равновесия для всех входящих в нее элементов. В данной ситуации представляется целесообразным записать уравнения для электрической сети и асинхронных двигателей в системе координат a, b, 0. Для синхронных двигателей можно воспользоваться системой полных уравнений Парка-Горева, записанных в координатах d, q, 0, жестко связанной с ротором каждого двигателя. Необходимо только добавить уравнения связи между системами координат d, q, 0 каждого двигателя и a , b, 0.
Положение секционного выключателя (СВ) произвольное и может измениться в любой момент времени переходного процесса. Все без исключения двигатели моделируются по полным уравнениям, — как нормально работающие в установившемся режиме, так и участвующие в пуске или самозапуске.
1 Выполняется ввод исходных данных об эквивалентной системе и двигателях, задается начальное и конечное время расчета переходного процесса. Для двигателей также задаются начальные условия и шаг вывода результатов расчета.
2 Для всех двигателей по известным начальным условиям определяются составляющие токов в координатных осях a, b, 0 для начального момента времени расчета переходного процесса — ia(t+0)i,ib(t+0) . Если не заданы ia(t-0)i, ib(t-0)i , то при тех же начальных условиях определяются ia(t+h)i, ib(t+h)i где h — шаг численного интегрирования и дифференцирования.
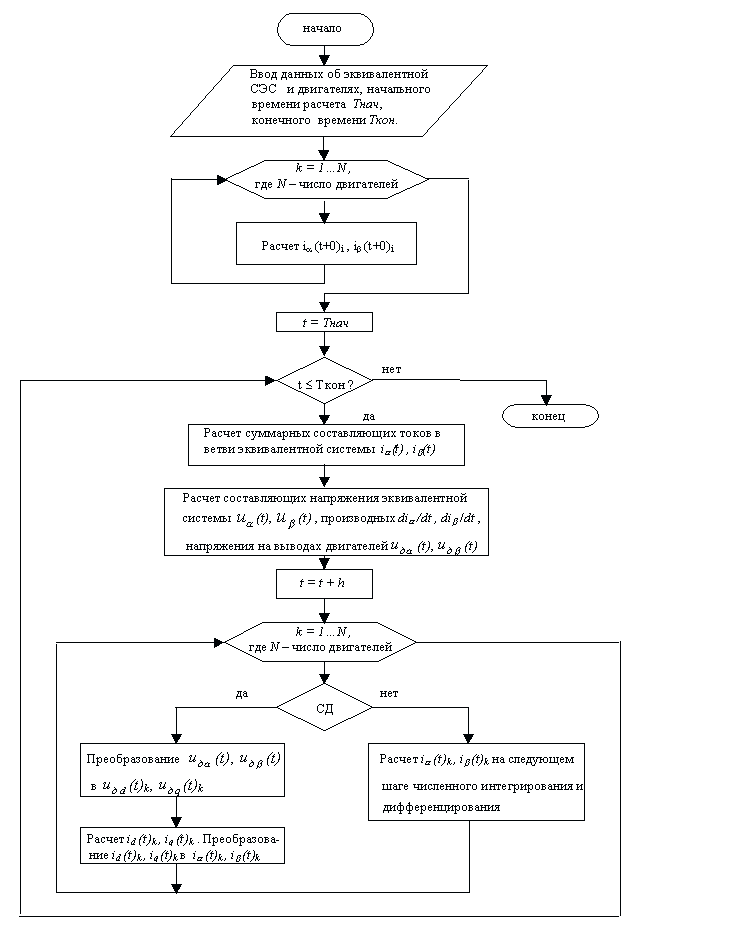
3 Определяются суммарные составляющие токов в ветви эквивалентной системы — ia, ib для текущего момента времени.
4 Для момента времени t рассчитываются составляющие напряжения эквивалентной системы ia, ib, значения производных 
и далее — составляющие напряжения на выводах двигателей.
5 Для всех двигателей по известному напряжению на выводах определяются составляющие токов ia(t)i, ib (t)i на следующем шаге численного интегрирования и дифференцирования. Следует отметить, что для СД на этом шаге дополнительно выполняются преобразования составляющих напряжения на выводах из координат a, b, 0 в d, q, 0 каждого двигателя и составляющих тока из d, q, 0 в a ,b, 0. Преобразования могут быть выполнены по выражениям, приведенным в [1].
6 Осуществляется переход к пункту 3 до тех пор, пока не будет достигнуто конечное время расчета.
На основе предложенной модели разработана программа для персонального компьютера.
Выполнить апробацию предложенной модели путем сравнения результатов моделирования переходных процессов в многомашинной системе с результатами эксперимента достаточно сложно, так как представляет серьезные трудности осциллографирование параметров нескольких двигателей одновременно. Апробация модели проводилась путем сравнения результатов расчетов переходных процессов одиночного пуска и самозапуска СД 4,8 МВт по предложенной модели, с экспериментальными осциллограммами. Погрешность моделирования не превышает 10% при экспериментальном определении параметров двигателя.
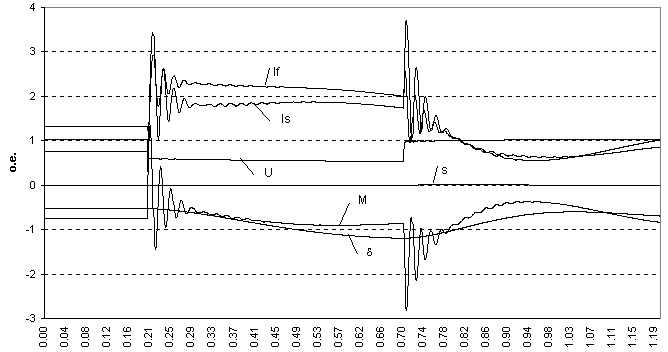
В качестве примера использования предлагаемой модели выполнен расчет переходного процесса в системе электроснабжения, состоящей из внешней сети и двух СД мощностью 4,8 МВт и 1,5 МВт, подключенных к общим шинам, при возмущении, вызванном понижением напряжения сети до 0,55Uном в течение 0,5 с и последующем его восстановлении. Результаты моделирования представлены на рис.3. На нём: IS — модуль обобщенного вектора тока статора по отношению к амплитуде номинального фазного тока статора, о.е.; U — модуль обобщенного вектора напряжения на выводах двигателя, о.е.; М — электромагнитный момент двигателя по отношению к базисному моменту (большему номинального в 1,34 раза для СД 1,5 МВт и в 1,157 раза для СД 4,8 МВт), о.е.; If — ток возбуждения, выраженный во взаимной системе относительных единиц; s — скольжение; d — угол между синхронной осью и поперечной осью ротора, рад
Предложенная модель позволяет с достаточной для практических целей точностью выполнить анализ взаимосвязанных электромеханических и электромагнитных переходных процессов в многомашинной системе с расчетом мгновенных значений режимных параметров и оценить взаимное влияние двигателей и сети.
Модель и программа разрабатывались для простейшей расчетной схемы с единственной целью — избежать ошибок при разработке модели и отладке программы. Все положения, полученные при разработке модели, могут быть обобщены для многомашинной системы произвольной конфигурации.
1. Применение аналоговых вычислительных машин в энергетических системах. Методы исследования переходных процессов / Под ред. Н.И.Соколова. Изд. 2-е, перераб. и доп. М.: Энергия, 1970. — 400 с.