Источник: Всеукраинская научно – техническая конференция студентов «Электротехника, электроника и микропроцессорная техника», 26 - 27 мая 2010 г., ДонНТУ
Аннотация:
Колесников Р.В., Мельник А.А. Математическая модель асинхронного двигателя с учетом вытеснения тока в фазных координатах. Розроблено математичну модель короткозамкненого асинхронного двигуна з урахуванням ефекту витиснення струму в стержнях ротору для використання у складі частотно – регулює мого приводу промислових механізмів. Реалізована математична модель в структурних блоках пакету Matlab/Simulink, яка дозволяє використовувати її для проведення наукових досліджень та вирішення практичних завдань.
Введение.
Среди основных задач в области моделирования электротехнических устройств и процессов на сегодняшний день является отказ от принимаемых ранее допущений, пренебрежения физическими процессами, протекающими в реальных устройствах и аппаратах. К одному из таких допущений следует отнести эффект вытеснения тока в стержнях ротора асинхронного двигателя.
Цель работы.
Разработать математическую модель короткозамкнутого асинхронного двигателя с учетом эффекта вытеснения тока в стержнях ротора и реализовать последнюю в структурных блоках пакета Matlab/Simulink для работы в составе частотно-регулируемого привода.
Материал и результаты исследований.
Задача учета эффекта вытеснения тока может быть успешно решена, если будем полагать известными зависимости R2=f(s) и X2=f(s) при частоте питающей сети f1=50 Гц полученные экспериментальным путем.
Имеющиеся массивы данных, следует аппроксимировать полиномом вида:
В отличие от работы [1] необходимо соотнести значения R2 и X2 со скольжением во всем возможном диапазоне изменения последнего, включая переходные режимы рис.1.
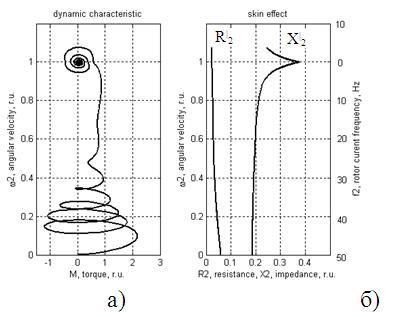
Рисунок 1 – Динамическая механическая характеристика (а) и соответствующие ее координатам значения активного и реактивного сопротивления ротора (б).
Для области значения скорости сверх скорости идеального холостого хода, примем зеркальное отражение функции R/2=f(s) и X/2=f(s) ,что не противоречит физическим процессам, имеющим место в обмотке ротора в динамике.
Выбор координатных осей для обмотки статора для моделирования поведения машины переменного тока не является однозначным. С одной стороны, чтобы получить дифференциальные уравнения равновесия напряжений с постоянными коэффициентами при неизвестных, рекомендуют применять такую ортогональную систему координатных осей, в которой преобразованные контуры обмоток статора и ротора взаимно неподвижны. С другой стороны, для учета явления эффекта вытеснения тока необходимо выполнять подстановку значений (1) соответствующих текущему значению скольжения на каждом шаге численного интегрирования, что возможно только для трехфазной системы координат [3].
С учетом вышеизложенного, запишем основные уравнения в матричном виде:
где US, IS, ?S, Ur, Ir, ?r – векторы напряжений токов и потокосцеплений фаз А, В, С статора и a, b, c ротора;
Rs, – матрица активных сопротивлений фаз статора;
Rr(s) - матрица активных сопротивлений фаз ротора приведенных к статору, соответствующих текущему значению скольжения;
I0, ?0 – объединенные векторы токов и потоков (статора и ротора).
Модель исследуемой системы, записанная согласно с (2) в структурных блоках пакета Matlab/Simulink имеет вид, представленный на рис.2. Для работы модели необходимо использовать пять функций пользователя, опуская листинги, укажем назначение функций в табл. 1.
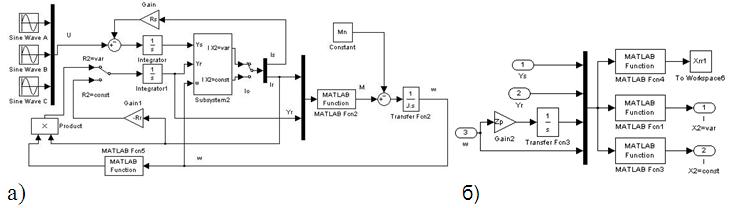
Рисунок 2 – Математическая модель асинхронного двигателя в естественной системе координат с учетом эффекта вытеснения тока в стержнях ротора а) подпрограмма Subsystem б) в структурных блоках пакета Matlab/Simulink.
Предложенная модель, прежде всего, позволит оперировать с истинными, полученными экспериментально, значениями активного R/2 и реактивного X/2 сопротивлений для текущего значения скольжения при заданных величине и частоте питающего напряжения, что существенно приблизит значения вычислительного эксперимента натурному, кроме того, такая модель позволит исследователю уточнить значения максимального момента и критического скольжения при работе на искусственных характеристиках для заданного закона частотного регулирования.
Выводы.
1. Разработана математическая модель асинхронной машины с учетом эффекта вытеснения тока в стержнях короткозамкнутой обмотки ротора на основе экспериментально полученных зависимостей R2=f(s) и X2=f(s).
2. Разработанная математическая модель асинхронной машины может быть использована для моделирования частотно-регулируемого привода на базе последней для известных законов регулирования.
Литература
- Каваре Ясер Хусейн. Учет эффекта вытеснения тока в стержнях ротора асинхронного двигателя при его моделировании в среде Matlab. Наукові праці Донецького національного технічного університету. Серія: «Електротехніка і енергетика», випуск 67: Донецьк: ДонНТУ, 2003. – С.160-162.
- Сивокобыленко В.Ф. Моделирование режимов работы асинхронных машин с учетом насыщения магнитных цепей и вытеснения токов в роторе. Наукові праці Донецького національного технічного університету. Серія: «Електротехніка і енергетика», випуск 112: Донецьк: ДонНТУ, 2006. – С.10-16.
- Моделювання електромеханічних систем: Підручник/ Чорний О.П., Луговой А.В., Родькин Д.Й., Сисюк Г.Ю., Садовой О.В. – Кременук, 2001. – 376 с.
- Макаров К.Д., Акульшина Л.И., Гайдашева Л.Я., Городько О.Ю. О регулировании напряжения на зажимах частотно-регулируемого асинхронного двигателя. Взрывозащищенное электрооборудование: Сб. науч. тр. УкрНИИВЭ / Под общей ред. д-ра техн. наук, профессора В.С.Дзюбана.- Донецк: ООО «Юго-Восток, Лтд», 2005. - 320 с.
- Мельник А.А. Численное моделирование процесса частотного пуска асинхронного двигателя с учетом эффекта вытеснения тока в стержнях ротора в среде Matlab // Вісн. Кременчуцьк. держ. політехн. ун-ту імені Михайла Остроградського. – Кременчук: КДПУ, 2008. – Вип. 4 (51), ч. 2. С. 78–82.