Моделирование релевантных регулируемых переменных для электромеханического травления
R. Neugebauer, H. KnAupfer, K. Wolf, and H.-J. Roscher
Перевод с английского: Колесников Р.В.
ВВЕДЕНИЕ
Электромеханическое травление, вид электрохимических станков (ЭХС) – это технический станок, который удаляет метал, что достигается посредством управления процессом растворения. Это выполняется благодаря раствору соли и источника тока. Подсоединяют предмет с положительным полюсом и электрод к проводящему отрицательному полюсу. См. рис. 1. Когда электроны текут от минуса через соль посредством ионов к плюсу, метал (рабочая зона) разъедается.

Рисунок 1 – Электрохимический станок (ЭХС) – процесс.
Современный уровень для регулировки размера зазора используется механизированный привод. Привод двигателя в виде кулачкового вала обеспечивает синусоидальную кривую ширины зазора в течении длительного времени. Зазор прямоугольной формы в течении коротких периодов должен быть оптимальным. Кроме того, привод двигателя приближает большие требования к мощности электрического двигателя и высоких усилий для точности позиционирования маленького растягивания пружины. Для решения этих проблем высокая динамика актуаторов, например пъезо – блоки, может быть использована потому что они могут действовать с относительно высокой частотой и высокой точностью пока обеспечивается высокая реакция сил и необходимый удар.
Для проверки практичности различных актуаторов были выполнены моделирования, которые представлены в первой части. Эта часть также представляет физическую модель системы, от которой выведены дифференциальные уравнения и Simulink – модель. Характеристика системы и выводы относительно размеров некоторых входных параметров рассмотрены в следующей секции. И на конец, последняя часть представляет выводы и обзор.

Рисунок 2 – Электрохимический станок
2. Колеблющийся привод – модель и решение
2.1. Модель пъезо – основы колеблющегося привода
Пъезо – основы колеблющегося привода состоят из линейного привода с большой массой, пъезо актуатора с жесткостью с и электрод с добавочной массой m (см. рис. 3). Пъезо – блок совершает синусоидальные колебания, которые совмещаются с перемещением линейного привода z0, в результате дают полное возбуждение
Далее масса линейного привода большая по сравнению с оставшейся системой, z0 может быть предположен постоянным.
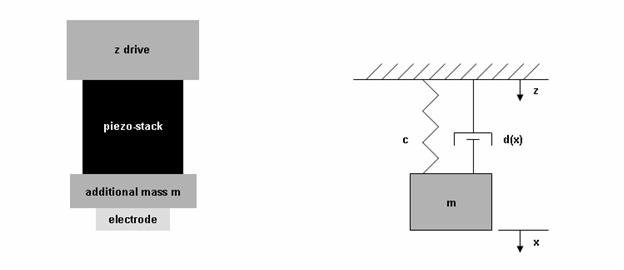
Рисунок 3 – Модель пьезо – основы колеблющегося привода
Инертные силы массы m и сил сжатия Fsqueezing жидкости в рабочем пространстве сжимающих или растягивающих пружину с в системе пружина – масса разностью возбужденного движения z и движением х массы m, к которой прочно присоединена:
Сила сжатия действует как сильный нелинейный демпфер и может быть аппроксимирован на составляющие
где А описывает площадь поверхности электрода и n динамику вязкости жидкости (смотри [1]). Площадь поверхности, которая зависит от ширины зазора, но рассмотрена как постоянная, отмеченная как добавочный поток сопротивления.
Последующее дифференциальное уравнение может быть выведено из равнений (2) и (3):
Основанная на уравнении (4) была построена Simulink модель, которую можно увидеть на рисунке 4.
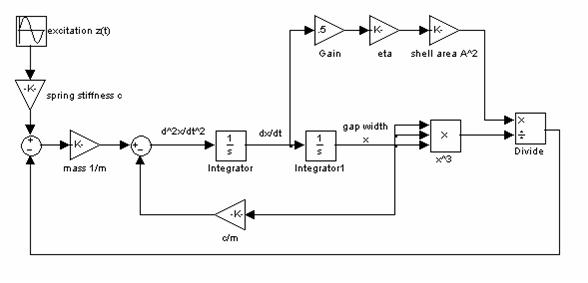
Рисунок 4 – Simulink модель пьезо – основы колеблющегося привода.
2.2 Результаты
Для первого моделирования установлены следующие параметры.
- Амплитуда синусоидального возбуждения zp=100 mum
- Частота возбуждения f=50 Hz
- Начальное положение z0=110 mum
- Площадь поверхности корпуса равный площади поверхности электрода А = 141,4 mm * 141,4 mm = 20000 mm^2
- Динамика вязкости жидкости n = 0.001 Pa*s (вода)
- Масса m = 50 kg
- Жесткость пружины пьезо – актуатора c = 300 N*mum^-1
Результаты моделирования можно увидеть на рисунке 5.
Смотря на график ширины зазора прямоугольный вид возможен. Минимальный рабочий зазор около 40 микрометров и нуждается в уменьшении. Система сил, т.е. сила пружины, ведомая силой инерции и сжимающей силой, также изображена на рисунке 5.
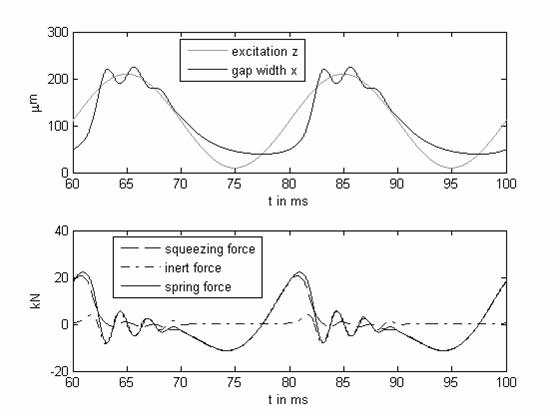
Рисунок 5 – Результаты моделирования системы первыми установками.
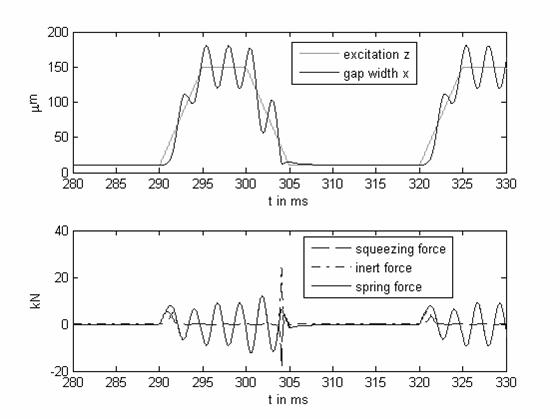
Рисунок 6 – Результаты моделирования системы с маленькой площадью поверхности и трапециевидным возбуждением.
Потому что маленькая масса, сила инерции относительно мала и сила пружины, быстро колеблющейся.
Для улучшения свойств системы был изменен параметр. Изменение жесткости пружины имеет значительное влияние на ширину зазора. Увеличения жесткости пружины приводит к уменьшению ширины зазора и уменьшению колебаний в течении открытой фазы. Изменение частоты возбуждения не приводит к значительному уменьшению зазора, но уменьшает площадь поверхности. Увеличение массы приводит к увеличению кинематической энергии. Большая сила инерции приводит к уменьшению вибраций силы пружины. Влияние массы намного более сильнее в открытой фазе, потому что с силой инерции также сила сжатия увеличивается когда сходятся электроды.
Площадь поверхности 1600 mm^2 и трапецеидальное возбуждение с периодом времени 30 ms результируются в ширине зазора, которая задерживается на 17 миллисекунд на 10 микрометрах и открывается в среднем 150 микрометров (см. рис. 6).
Выводы и обзор
Как видно из моделирования, реализация пьезо – основы колеблющегося привода является очень перспективной. Далее предполагаемая жесткость пружины пьезо – актуатора на столько хороша на сколько масса электрода имеет реалистичные значения, они сохраняются. Рабочий зазор может быть принужден к относительным постоянным, вызванным нелинейностью системы и применении частоты привода, которая имеет преимущество над резонансной частотой. К тому же, трапецеидальное возбуждение выполненное пьезоактюатором разумно для желаемой ширины зазора. Большие силы реакции ограничивают минимальный рабочий зазор приблизительно на 10 мкм при относительно ен большой площади поверхности электрода. В результате открытый зазор должен быть достаточно большим для промывки.
Следующим шагом является проверка результатов моделирования, делая измерения системы. На основе результатов модель может быть улучшена путем рассмотрения массы пьезо – стека и линейного привода, а также его жесткости. Кроме того, площадь поверхности может быть рассчитана в зависимости от ширины зазора и должна быть использована реальная динамическая вязкость жидкости.
Ссылки
- Kurth, S., "Theoretische und experimentelle Verhaltensbeschreibung kinetischer mikromechanischer Komponenten mit elektrostatischer Feldkopplung", Dissertation TU Chemnitz, D,1995.
- Griffin, W. S., H. H. Richardson, and S. Yamanami, "A study of fluid squeeze-film damping", ASME J. Basic Eng., 451-456, 1966.
- Mc Geough, J., Principles of Electrochemical Machining, Chapman & Hall, London, UK, 1974.
- www.pemtec.de.