Источник: http://www.v–itc.ru/electrotech/2011/01/pdf/2011–01–01.pdf
Предложена методика математического моделирования электрической системы, основанная на прямой идентификации по полной нелинейной математической модели электроэнергетической системы. Представлены результаты компьютерного моделирования, подтверждающие применимость методики для решения практических задач, возникающих при испытании и настройке систем управления.
Ключевые слова: газотурбинная электростанция, электрическая нагрузка, идентификация, испытания.
Статья выполнена при поддержке субсидии по постановлению Правительства Российской Федерации от 09.04.2010 г. № 218 (проект «Создание высокотехнологичного производства для оказания услуг по испытаниям газотурбинных установок мощностью до 40 МВт на многоцелевом адаптивном экологичном стенде»).
Газотурбинные авиационные установки (ГТУ) обладают свойствами, обеспечивающими возможность их широкого применения в наземных условиях в качестве привода электрогенераторов для выработки электроэнергии. Вместе с тем в области «малой энергетики» продолжают сохраняться определенные проблемы [1]. Несмотря на то, что в нашей стране сегодня разрабатывается и эксплуатируется примерно 20 типоразмеров малых ГТУ от 1 до 25 МВт [2], внедрение отечественных миниэлектростанций идет пока в целом невысокими темпами. Так, одна из первых в России муниципальная газотурбинная электростанция (ГТЭС) «Шигили» полностью на российском оборудовании была построена лишь в 2000 г. Тем временем на российской территории активно внедряются многочисленные импортные разработки, например автономные газотурбинные установки – электростанции «Turbomach», «Siemens», «Alstom» и др. Эти станции уже размещены во многих регионах России и СНГ, в том числе у нефтяников и газодобытчиков (ОАО «ЛУКОЙЛ», ТНК–ВР и газовых месторождениях ОАО «Газпром»), где утилизируют и перерабатывают попутный нефтяной газ и, добавим, успешно вытесняют отечественного товаропроизводителя. Положительный момент этой ситуации состоит в том, что она заставляет наших разработчиков проводить более активную политику по совершенствованию характеристик своих изделий. В частности, длительное время проблемой был ограниченный ресурс российских ГТУ. Сейчас эта проблема практически снята, но остается ряд других проблем.
Сегодня актуальна задача существенного повышения характеристик вырабатываемой электроэнергии. Для этого необходимо совершенствовать системы автоматического управления (САУ) ГТУ.
В настоящее время при проектировании САУ энергетических ГТУ работа САУ электрогенераторов и электроэнергетическая система (ЭЭС) в целом не учитывается или учитывается приближенно. Более того, САУ ГТУ продолжают строиться главным образом на основе прежних авиационных прототипов. САУ ГТУ и САУ синхронных генераторов проектируются раздельно, и согласование их характеристик происходит лишь на завершающих стадиях разработки мини–электростанции.
Проблема усложняется тем, что в составе ГТЭС функционируют до 8 и более энергоблоков ГТУ, которые могут работать одновременно. При этом они должны обеспечивать различные режимы работы: автономный, параллельный, на мощную сеть, с преобладанием разнородной по составу электрической нагрузки и др. Все эти вопросы необходимо учитывать при проектировании САУ и последующей ее отладке и настройке. Существующие требования испытаний являются достаточно жесткими [3], но нельзя считать их исчерпывающими. Испытания в динамике в настоящее время проводятся при сбросах–набросах в ограниченных пределах статической нагрузки со стороны электрогенератора, что не учитывает многообразия перечисленных выше режимов ЭЭС. Натурные испытательные стенды представляют собой обычные серийные электростанции, нагружаемые полем активных сопротивлений. Такие стенды обладают ограниченной функциональностью, в частности, они не способны воспроизводить режимы работы на мощную сеть и параллельные режимы работы, которые, как известно, достаточно проблемны с точки зрения задач управления.
Таким образом, решение проблемы повышения качества электроэнергии следует искать в проведении комплексных компьютерных и полунатурных испытаний проектируемых САУ энергетических ГТУ с учетом ЭЭС, представленной в виде математической модели. Для этого необходимо разработать многофункциональную математическую модель ЭЭС. Полная модель ЭЭС содержит в своем составе модели отдельных структурных элементов (электрогенераторов, электродвигателей, линий связи, статических нагрузок, трансформаторов, мощной сети, систем автоматического регулирования и др.).
Кроме того, модель ЭЭС должна предоставлять возможность воспроизведения различной топологии ЭЭС и модифицировать состав ее структурных элементов. Использование такой модели позволяет исследовать режимы (прежде всего предельные режимы), которые невозможно воспроизвести в ходе экспериментов на реальной ЭЭС. Для этого согласно классификации [4] модель должна относиться к 1–му классу точности, т.е. процессы в генераторах описывать полными уравнениями Парка–Горева, учитывать демпферные обмотки, системы регулирования ГТУ и возбуждения генераторов.
Но это означает, что математическая модель только одного генератора представляет собой систему алгебраических и нелинейных дифференциальных уравнений 8–10–го порядка. Если исследуемая ЭЭС содержит несколько генераторов, электродвигателей и других элементов, то даже применение современной компьютерной техники требует значительных затрат времени, поскольку из-за воспроизведения сверхпереходных составляющих статорных токов шаг численного интегрирования выбирается, как правило, не более 10 мкс. В результате, например, характерный переходный процесс реальной продолжительностью 1 секунда для системы из 6 параллельных энергоагрегатов и распределенной комплексной электрической нагрузки рассчитывается с помощью одноточечного метода Рунге–Кутта четвертого порядка за 14,6 минут на базе Pentium IV, 3 GHz персонального компьютера [5].
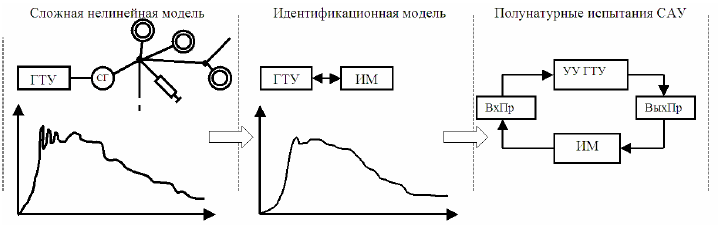
Главное преимущество сложной модели состоит в том, что она позволяет получить все основные характерные режимы ЭЭС. При этом результаты расчета по полным уравнениям всегда более достоверны, чем результаты расчета по упрощенным уравнениям [4]. Но по причине невысокого быстродействия непосредственное использование сложной модели в задачах испытания и настройки САУ весьма затруднительно. Для примера рассмотрим процесс компьютерной параметрической настройкиалгоритма управления САУ ГТУ (рис. 1).

Рис. 1 – Схема параметрической настройки алгоритмов САУ: УУ – устройство управления

Рис. 2 – Построение идентификационной модели (ИМ): ВхПр и ВыхПр – соответственно входные и выходные преобразователи
При выборе оптимальных настроек с целью обеспечения заданного качества переходных процессов в режиме стабилизации частоты и напряжения требуется многократное воспроизведение переходного процесса.
Для поиска оптимальной настройки могут применяться различные численные поисковые методы (симплекс-метод, покоординатный спуск, случайный поиск и др.), каждый из них требует затрат времени на эксперименты, а также последующую оценку их результатов на соответствие критериям качества. Отсюда ясно, что полная модель для этой цели малопригодна.
Еще большие сложности возникают при использовании так называемого «полунатурного моделирования» [6]. Здесь требования к быстродействию моделей еще более строгие, модели должны работать в темпе с испытуемым реальным объектом (натурные агрегаты САУ ГТУ, как правило, вырабатывают сигналы с периодом от 0,01 до 0,05 с). Таким образом, для решения указанных задач необходима определенная иерархия моделей, включающая как минимум два уровня: сложная модель для выявления характерной динамики и упрощенная модель для настройки алгоритмов САУ и полунатурных испытаний. Упрощенную модель целесообразно формировать на основе полной модели (рис. 2).
Указанное упрощение сложной модели, по сути, является хорошо известной задачей эквивалентирования. Но в силу того, что исходная сложная модель является нелинейной, строгое эквивалентирование невозможно, а приближенное эквивалентирование требует априорной информации (которую следует извлекать из исходной сложной модели). По этой же причине допустимыми являются два подхода: эквивалентирование на основе исключения переменных и эквивалентирование на основе идентификации [7]. В статье рассматривается второй подход, поскольку существенным для решаемых задач (испытания и настройки САУ ГТЭС) является «внешнее» поведение ЭЭС, задаваемое ее внешними динамическими характеристиками.
В Пермском государственном техническомуниверситете по заказу промышленности разработана сложная динамическая нелинейная модель ЭЭС в составе программного комплекса для испытания алгоритмов управления. Кратко поясним основные свойства этой модели [8].
Сложная модель состоит из двух уровней: модели элементов и модели их взаимодействия. Модель каждого структурного элемента
ЭЭС, несмотря на существенные внутренние отличия, описывается единообразно в форме векторно-матричного уравнения:
pI=+(-)AU - BI - H, (1)
где I, pI – вектор токов и вектор производных токов элемента; U – вектор напряжений, приложенных между внешними зажимами
элемента; A, B – матрицы, размерность которых зависит от системы координат в которых моделируется структурный элемент, а также от того пол-
ные это уравнения или упрощенные; H – вектор, определяющий воздействие на элемент со стороны средств регулирования электрических параметров.
Математическая модель взаимодействия структурных элементов использует матрицу инцидентности M, отражающую топологию рассматриваемой локальной системы электроснабжения:

где M – клеточная матрица инцидентности, клетками матрицы являются единичные, нулевые матрицы или матрицы преобразований координат; MT – транспонированная матрица
инцидентности; G – блочная матрица проводимостей ветвей (элементов), образующих систему; W – вектор, полученный из правых частей уравнений элементов в (7); M' – матрица, элементами которой являются нулевые клетки или
клетки производных элементов матриц преобразования координат; U – вектор искомых напряжений узлов.
Представление математических моделей в (1) и (2) открывает возможность для получения идентификационных моделей. Разработанная методика построения быстрорешаемой идентификационной модели включает три основных этапа:
Идентификационные модели обычно ищутся в следующем виде [7]: Y=AX, (3)
где Y – вектор выходных переменных; X – вектор входных переменных; A – матрица коэффициентов, размерностью nxn, которую следует идентифицировать.
Если в результате наблюдений над сложной нелинейной моделью известны n векторов Y и X, то матрица A может быть идентифицирована
по n наблюдениям: (4)
(4)
где Yсум и Xсум – матрицы, составленные из n векторов Y и X соответственно.
Если наблюдений больше чем n, применяется метод наименьших квадратов: (5)
(5)
Рассмотрим один из возможных способов идентификации, который состоит в преобразовании системы (3) к виду:
I(k)=A(k)U(k) , (6)
где I(k) – вектор выхода на k-м промежутке расчета; A – идентифицируемая матрица постоянных коэффициентов; U(k) – вектор входа на k-м
промежутке расчета.
Главная особенность модели (6) состоит в том, что она описывает статический режим. Воспроизведение динамики с помощью модели (6) возможно на основе концепции мгновенных схем [7], при этом на отдельном относительно малом промежутке времени все переменные I, U считаются постоянными. Тем самым производится редукция исходной динамической модели к набору статических. В дальнейшем будем называть этот подход квазидинамическим.
В качестве внешних динамических характеристик выбраны внешние (статорные) токи узла нагрузки, составляющие вектор I = (Id, Iq)T, и напряжение узла нагрузки, также составляющее вектор U = (Ud, Uq)T. Двухкомпонентность векторов позволяет учесть и восстановить активную и реактивную составляющую мощности нагрузки по результатам расчета переходного процесса и получить другие параметры (угол нагрузки, коэффициент мощности и пр.). Например, активная мощность P = Ud Id+Uq Iq, реактивная мощность: Q = –Uq Id +Ud Iq.
В силу того, что идентификация выполняется по внешней характеристике, получаемая идентификационная модель в общем случае не
представима в виде какой-либо электрической цепи. Например, при эквивалентировании системы, состоящей из двух асинхронных
двигателей (АД), двух синхронных генераторов (СГ), одной линии связи и двух статических нагрузок, получилась следующая матрица А эквивалентной системы:

Эту матрицу можно было бы считать матрицей статической нагрузки:

но этому препятствует то, что активные и индуктивные сопротивления не равны между собой, и, кроме того, одно из активных
сопротивлений отрицательно. Впрочем, в том случае, если требуется получить реальное физическое представление (например, для
воспроизведения на натурном стенде), достаточно модифицировать алгоритм идентификации. Покажем,как это можно сделать.
Пусть вектор
R=(rН , шxН)tr – вектор параметров статической нагрузки, и пусть I = (Id, Iq)tr – вектор тока,U = (Ud, Uq)tr – вектор напряжения.
Тогда с учетом (7) можно записать:
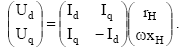
Если используются n измерений, то размерность первого вектора становится 2nx1, второй матрицы – 2x2n, последний вектор остается прежним с размерностью 2x1.
Асинхронная двигательная нагрузка играет особую роль в ЭЭС, поскольку их пусковой режим существенно влияет на режим электрической системы. При соизмеримой мощности двигателей и генераторов системы проверка влияния пуска двигателей на режим системы должна производиться в обязательном порядке [4].
Рассматривается пуск АД от соизмеримого по мощности СГ (мощность АД составляет 30 % от мощности СГ), кроме того, к узлу нагрузки подключена незначительная по мощности активноиндуктивная нагрузка. Пуск АД не может быть идентифицирован одной матрицей A (7). Это связано с тем, что в параметры АД входит скольжение S, которое меняется при пуске от 1 до 0.
На рис. 3, а для сравнения показан пуск маломощного двигателя, при этом напряжение постоянно и характеристики представлены отрезками прямых.
На рис. 3, б и 3, в показан пуск соизмеримого по мощности АД, идентифицированного соответственно 5 и 20 матрицами А, при этом из-за снижения напряжения во время пуска (генератор принят нерегулируемым) переходный процесс идентификационной модели представлен отрезками кривых. Тонкими линиями выделены токи Id, Iq исходной сложной модели, жирными линиями – токи идентификационной модели. Требуется как минимум две матрицы А, чтобы учесть нестационарность исходной модели. В том случае если используется большее количество матриц, приближение, естественно, получается лучше.
Обусловленность матриц проверяется по критерию обусловленности Тюринга. Чтобы избежать плохой обусловленности при получении псевдообратной матрицы в случае медленного изменения переменных (режим приближается к установившемуся), целесообразно накладывать на входной сигнал дополнительный идентифицирующий сигнал малой амплитуды, приближающийся по своим характеристикам к «белому шуму».
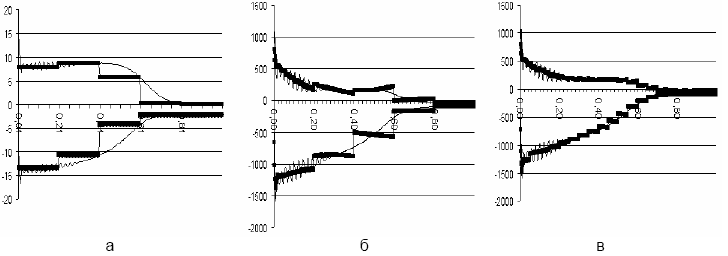
Рис. 3 – Идентификация процесса пуска АД
Результаты исследований позволяют сделать следующие выводы.