
Источник: http://esmo.kdu.edu.ua/statti/183.pdf
Вступ. Динамічна стійкість синхронних генераторів у реальних електроенергетичних системах порушується, як правило, досить швидко слідом за збурюванням – протягом 1 – 3 с. Тому розрахунки перехідних процесів, які мають за ціль аналіз динамічної стійкості електричних систем, використовують порівняно прості математичні моделі, де кожен генератор описується диференціальним рівнянням другого порядку, а обертаючий момент на його валу приймається незмінним. Частота в енергосистемі протягом усього перехідного процесу вважається незмінною.
Мета роботи. Зіставний аналіз математичних моделей турбогенераторів, які широко використовуються у програмному забезпеченні, на прикладі розрахунків асинхронного режиму генератора і зіставлення їх з досвідченими даними.
Матеріал і результати дослідження. При математичному моделюванні, так само як і при чисельних методах розрахунку перехідних процесів в обертових електричних машинах змінного струму, першим виникає питання про форму вихідних рівнянь. Рівняння можуть бути взяті у вихідній неперетвореній формі або перетвореними тим чи іншим засобом. Від виду рівнянь залежить не тільки кількість необхідної апаратури і її складі, але і наочність рішень і, навіть іноді, точність. Чим менше нелінійних елементів, тим вище точність рішень, тим легше налагоджується модель. Відомі лінійні перетворення вихідних рівнянь дозволяють виключити періодичні коефіцієнти в рівняннях і тим набагато спростити рішення.
Найбільш універсальним є перетворення до обертового разом з ротором і жорстко з ним зв'язаним осям координат d і q, що приводять до рівнянь Парка – Горєва. Вони придатні і для синхронних і для асинхронних машин, однак їхні переваги особливо яскраво виявляються при дослідженні процесів машин, що мають магнітну несиметрію ротора. Таке бачення в той же час і дуже “фізично”, оскільки процеси в подовжніх і поперечних контурах ротора слабко між собою зв'язані і можуть часто взагалі розглядатися незалежно. Для машин із симетричним ротором ці переваги значною мірою зникають і моделювання таких машин часто зручніше буває проводити при рівняннях, перетворених до осей, не зв'язаних жорстко з ротором. Однак для багатоконтурних на роторі машин, навіть бездоганно симетричних, кращим є моделювання по рівняннях, записаним в осях d і q, жорстко зв'язаних з ротором. При цьому практично одержати прийнятну точність рішення при моделюванні в будь – якій іншій системі координат, крім d і q, виявляється неможливим. При моделюванні можливі різні підходи до рішення задачі: можна безпосередньо розв'язувати вихідні рівняння Парка – Горєва або ж користатися схемами заміщення.
Синхронна машина – найважливіший елемент електроенергетичної системи. Поведінка синхронної машини істотно визначає характер електромеханічних перехідних процесів в енергосистемі. Математичне моделювання синхронної машини має деякі особливості, а саме виникає необхідність використання ієрархічно упорядкованого ряду моделей різного рівня точності з урахуванням зміни частоти у вузлі примикання машини до системи. Загальний метод побудови ієрархічно упорядкованого ряду моделей полягає в складанні спочатку найбільш повного для розглянутого класу процесів опису об'єкта і проведення його послідовних спрощень, що дозволяють одержати математичні моделі зниженої точності. Розглянемо даний метод на прикладі порівняно простої електропередачі, зображеної на рис. 1, у якій станція, що має місцевий вузол навантаження, зв'язана через лінію передачі з прийомною системою нескінченної потужності.

Рисунок 1 – Схема електричної мережі
Використання схем заміщення дозволяє застосовувати повні рівняння Парка – Горєва [1]. Тут основними моделюючими елементами є пасивні схеми, що відповідають схемам заміщення потокозчеплень машин. Виникаючі в схемах струми і напруги виявляються подібними моделюючим.
У роботі виконувались розрахунки перехідних режимів (асинхронного режиму генератора, який випав із синхронізму завдяки втраті збудження) із використанням математичних моделей генератора різної складності. Основний упор приділяється моделям, які формуються на основі рівнянь Парка – Горева. Розглянуті наступні математичні моделі генератора: 1 – модель по повним рівнянням Парка – Горева із використання багатоконтурних схем заміщення, 2 – модель по повним рівнянням Парка – Горева із використання схем заміщення з одним контуром, 3 – спрощена модель (в основу якої покладені рівняння руху генератора із використання асинхронного моменту, який отримано по багатоконтурній схемі заміщення).
Для опису динамічних властивостей масивних елементів ротора генератора використовувалися дві різноманітні схеми заміщення генератора. Для моделі по повних рівняннях Парка – Горєва – звичайна схема заміщення, а для спрощеної моделі – схема заміщення генератора з винесеним контуром намагнічування. Одна з основних відзнак схеми заміщення генератора з винесеним контуром намагнічування полягає в тому, що необхідне урахування зовнішнього опору у всіх параметрах схеми. Параметри еквівалентних багатоконтурних схем заміщення турбогенератора отримані по експериментальним частотним характеристикам.
Порівнянний аналіз проводився на прикладі генераторів: ТВВ – 200 – 2 при Р=152 МВт і замкнутої на Rcc=3,5·Rf ОЗГ; ТГВ – 200 при Р=124 МВТ і замкнутої на Rcc=7·R ОЗГ. У якості дослідних даних були прийняті іспити турбогенератора ТГВ – 200 на Бурштинській ГРЕС, наведені в [2] і ТВВ – 200 – 2, наведені в [3].
Аналіз зіставлення даних виконаний у процентному співвідношенні. Результати зіставлення приведені в табл. 1 – 2.
Таблиця 1 – Результати моделювання, що характеризують асинхронний режим турбогенератора ТВВ – 200 – 2

Таблиця 2 – Результати моделювання, що характеризують асинхронний режим турбогенератора ТГВ – 200
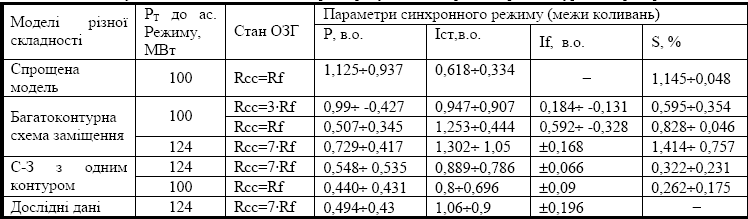
Як показує аналіз табл. 1 – 2 при ідентичному характері зміни режимних параметрів похибки розрахунку складають 5,5 процентів. Це обумовлено неточним визначенням параметрів ОЗГ при синтезі еквівалентних схем заміщення по частотних характеристиках провідності синхронних машин із боку обмотки статора. А також не завжди можна точно визначити величину базисного струму Iбf , через невірогідність у струмі Ifxx.
Збільшення похибки моделювання в режимних параметрах обумовлено неточною моделлю пристроїв АРШ, а також тим, що не враховується насичення сталі синхронної машини. Слід зазначити, що насичення сталі синхронної машини надає сильний вплив на зміну режимних параметрів під час перехідного процесу при навантаженнях Р=0,4 – 0,6 Рн.
Висновки. На підставі цього аналізу можна зробити висновок про недоцільність використання моделі генератора з одноконтурними схемами заміщення. Хоча багато промислових програм використовують такі моделі генератора і навіть більш спрощені, у яких фізичні процеси в роторі враховуються введенням демпферного коефіцієнта (класична модель).