
Джерело:
В останній час на основі повністю керованих ключів (GTO, IGBT) з'явився окремий клас перетворювачів частоти з безпосереднім зв'язком, що отримав назву матричний перетворювач частоти. Використання методів широтно-імпульсної модуляції робить матричний перетворювач конкурентноспроможнім по відношенню до перетворювачів з проміжною ланкою постійного струму та автономним інвертором напруги.
Матричний перетворювач з'єднується з навантаженням за допомогою дев'яти двонаправлених ключів. Також при керуванні перетворювачем необхідно дотримувати двох основних правил:
а) не повинні бути одночасно включені ключі, що з'єднують фази живильної мережі і фазу двигуна щоб уникнути короткого замикання;
б) хоча б один ключ, що з'єднує фази мережі і фазу двигуна повинний бути включений.

Система вхідних напруг перетворювача має вид:
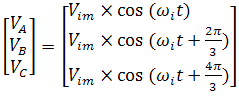
Вектор вихідних напруг матричного перетворювача може бути представлений:
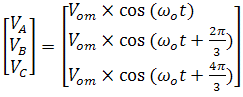
З формул (1) і (2) ?i і ?про відповідно частоті вхідної і вихідної напруги.
Якщо розглянути зв'язок між вхідними і вихідними напругами, то має місце залежність:
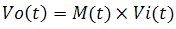
де M(t) – передатна матриця:

де:

– циклічний режим ключа SAa;
Ts – період роботи.
Вхідний струм дорівнює:
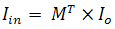
Циклічний режим повинний задовольняти наступним умовам щоб уникнути коротких замикань:
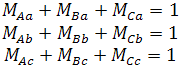
Це може бути реалізоване за допомогою алгоритму Вентуріні, що керує ключами SAa, SBa, SCa відповідно до бажаного вихідними напругою і частотою. Ключі, що формують напругу кожної фази двигуна замикаються по визначеному циклі.
Час циклу:
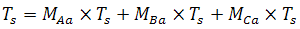
де

– частота переключення, що повинна бути якнайбільше, щоб мати низький гармонійний склад вихідної напруги.
Ключі керуються таким чином, що середнє значення вихідної напруги дорівнює бажаній напрузі за період Ts.
На основі викладених вище рівнянь будується математична модель матричного перетворювача частоти .
Необхідний коефіцієнт використання живильного напруги (q), вихідна частота (fo) і частота переключення (fs) – вхідні величини необхідні для розрахунку циклічного режиму матриці М. Цикл для коефіцієнта використання живильного напруги q=0.5 має вид:

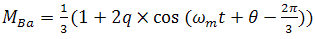

де

- частота модуляції;
teta - відповідна фаза виходу;
q – коефіцієнт використання живильного напруги.
Модель генератора керуючих імпульсів показана на рисунку 2. У даній моделі на вході порівнюються модуляційні функції з пилкоподібною напругою і далі надходять на вхід логічних елементів. Логічні ключі використовуються для одержання трьох сигналів, що пропорційні циклічному режиму силових ключів, для однієї фази вихідної напруги.

Блок Switch у пакеті MatLab працює по наступному принципу: він має 3 входи [in(1), in(2), in(3)] і 1 вихід і виконує логічну операцію: – if in(2)>0 then output=in(1) – else output=in(3).
Вихідними сигналами даної моделі є сигнали періодів замикання/розмикання силових ключів для формування фази вихідної напруги, що надходять на керуючі електроди транзисторів (рис.3).
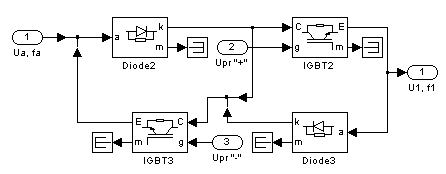
Замикаючи по визначеному алгоритму, силові ключі формують криву вихідної напруги однієї з фаз матричного перетворювача з відрізків кривих живильного напруги.
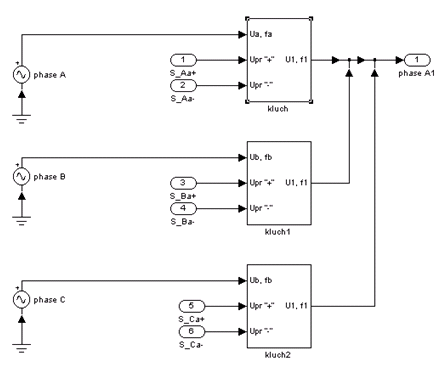

Таким чином, на базі існуючих рівнянь розроблена структурна схема МНПЧ у пакеті MatLab, що доповнена реальними напівпровідниковими елементами (транзисторами, діодами) з урахуванням їхніх властивостей.