Источник: Университет degli Studi di Bologna – Италия
Резюме. В этой статье представлено управление трехфазным матричным преобразователем с синусоидальными формами входных и выходных токов и единичным коэффициентом мощности на входной стороне. Стратегия управления была основана на использовании векторной модуляции. Этот подход имеет преимущество непосредственной логики переключений элементов. Максимальное значение V3I2 коэффициента передачи напряжения получена без рассмотрения третьего гармонического компонента напряжения. Число коммутаций в пределах периода цикла может быть ограничено, используя подходящую последовательность переключений. Кроме того, безопасное переключение достигнуто путем измерения тока. Было выполнено числовое моделирование полной системы, и представлены результаты, позволяющие проверить принцип управления.
Ключевые слова.Матричный преобразователь, Векторная модуляция.
Непосредственные преобразователи частоты получили значительное распространение с прогрессом в производстве силовых элементов. У матричных преобразователей есть следующие преимущества перед традиционными преобразователями частоты типа выпрямитель-инвертор:
Основные принципы стратегии модуляции матричных конвертеров были хорошо представлены в [1] и [2]. Максимальный коэффициент передачи напряжения равен ^3/2 для синусоидальных форм входа и выхода, и может быть получе, добавляя третьи гармонические компоненты напряжения к желательному выходному напряжению [2]. Другие исследователи также исследовали работу матричных преобразователей, используя конвертер PWM и принцип управления инвертором [3].
В недавно изданной статье [4] использовалась векторная модуляция (SVM), чтобы управлять матричным преобразователем частоты 3/3 с входным спектром тока фазы, подобным соответствующему спектру мостового диодного выпрямителя с 3 фазами. Эта работа представляет новый алгоритм управления, основанный на векторной модуляции, которая позволяет получить синусоидальную форму кривых на входе и выходе с единичным входным коэффициентом мощности. У векторного подхода к модуляции есть следующие преимущества относительно традиционной техники модуляции:
Кроме того, предложенный алгоритм переключения позволяет сократить количество переключающихся устройств, вовлеченных в процесс коммутации относительно обычных стратегий переключения [1], [2]. Нужно отметить, что поскольку стратегия модуляции определена непосредственно в терминах амплитуды и угла фазы на выходе, этот метод применим к высокоэффективным системам привода, таких как пространственная векторная модуляция. Проанализированная схема управления требует, чтобы измерение двух входных линейных напряжений определило отношение времени включенного состояния к периоду модуляции разрешенных комбинаций переключения. Кроме того, измерение двух линейных токов нагрузки позволяет реализовать безопасное переключение.

Эти особенности позволяют реализовать хорошую работу, даже при наличии несимметрии питающего напряжения, избегая введения малых гармонических составляющих в выходных напряжениях.
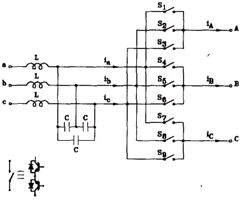
Общая топология трех фаз матричного инвертора показана на рисунке 1. Преобразователь состоит из девяти двунаправленных переключателей, которые позволяют любой фазе нагрузки быть связанной с любой входной фазой. Будучи преобразователем, питаемым источником напряжения, входные фазы никогда не должны замыкаться накоротко и, вследствие присутствия индуктивной нагрузки, выходные токи не должны прерываться. С этими ограничениями в матричном преобразователе 3/3 есть 27 разрешенных комбинаций открытых ключей. Для каждой комбинации, линейные напряжения входа и выхода могут быть выражены в виде пространственных векторов
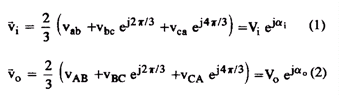
Таким же образом, линейные токи на входе и выходе имеют вид

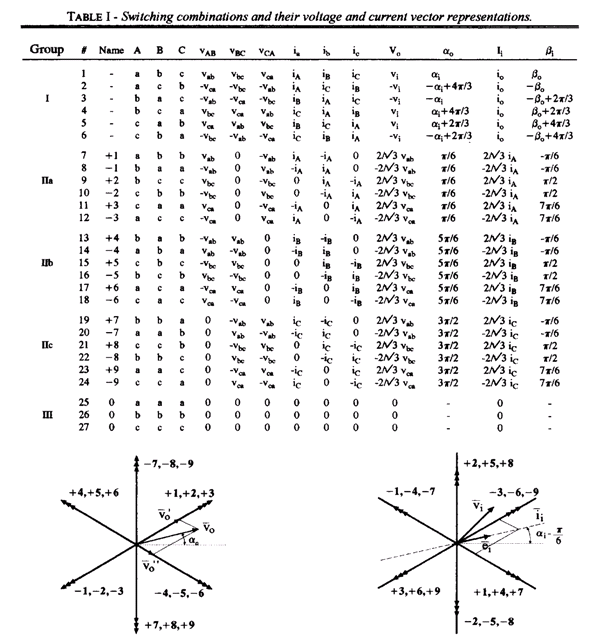
В таблице 1 показаны все разрешенные комбинации переключений. Для каждого из них дано получаемое линейное напряжение нагрузки как функция входных линейных напряжений, получаемый входной линейный ток выражен как функция линейных токов нагрузки. Как можно увидеть в таблице 1, для 6 комбинаций группы I каждая фаза нагрузки связана с различной входной фазой. В 18 комбинациях группы II, две фазы нагрузки замкнуты накоротко. В 3 комбинациях группы III все выходные фазы замкнуты накоротко. Каждая комбинация группы I определяет вектор выходного напряжения, имеющий фазу alfa0, который зависит от угла фазы alfa; из соответствующего вектора входного напряжения. Таким же образом, входной вектор тока имеет фазу beta, который связан с углом фазы beta0 вектора тока нагрузки. Следовательно, эти комбинации не могут полезно использоваться, чтобы применить технику SVM.
С другой стороны, 18 конфигураций группы II определяют шесть преднеподвижных положений вектора места выходного напряжения (рисунок 2), которые не зависят от alfa. 18 конфигураций группы II определяют также 6 преднеподвижных положений входного вектора места тока (рисунок 3), которые не зависят от beta0. Наконец, 3 конфигурации группы III определяют нулевое выходное напряжение и нулевые входные векторы тока.
Цель предложенной стратегии управления состоит в том, чтобы произвести желательный вектор выходного напряжения с обеспечением единичного коэффициента мощности. С этой целью, пусть v0 будет желательным вектором места линейного напряжения нагрузки V (Рисунок 2 и 3).
Входное фазное напряжение описывается вектором e, определено следующим соотношением

Чтобы получить на входе единичный коэффициент мощности, направление входного места тока I должно быть то же самое что и e.
На рисунке 2 vo' и v0" представляют компоненты v0 вдоль двух смежных векторных направлений. Вследствие маленького изменения входного напряжения во время переключающегося периода цикла желательный vo' компонент может быть получен, используя две переключающихся конфигурации, соответствующие двум векторам в том же самом напрвлении vo" и одной нулевой конфигурации напряжения. Среди шести возможных конфигураций переключения выбраны два представляющих более высокие значения напряжения и соответствие вектору vo'. Таким же образом используются две различных конфигурации переключения и одна нулевая конфигурация.
Для примера, показанного на рис. 2 и 3, входное напряжение V имеет угол фазы
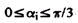
В этом случае напряжения линии vab и -vca принимают наибольшие значения. Тогда, согласно таблице 1, конфигурации можно получить как получать vo', +1 и -3, в то время как для vo"-4 и +6. Эти четыре конфигурации могут быть использованы, чтобы определить входное векторное направление тока. Фактически, как это показано на рис. 3, эти конфигурации связаны с направлениями вектора смежными с входным векторным положением тока.
Применяя векторную методику модуляции частота включения 5 может быть получена из каждой конфигурации, решая две системы алгебраических уравнений. В частности использование конфигураций +1,-3, чтобы произвести vo' и установить входной ток направляет ток, и мы можем написать
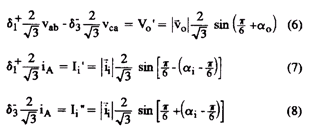
Рассмотрение уравновешенной системы синусоидальных напряжений сети, выраженных как
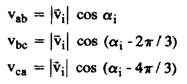
Выражение 6 может быть написано следующим образом
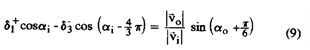
Объединяя выражения 7 и 8 получаем
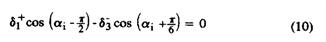
Решение системы уравнений 9 и 10 дает
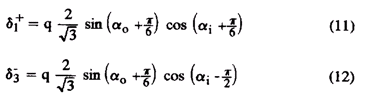
где
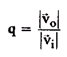
является коэффициентом передачи напряжения.
Выражения 11 и 12 могут быть переписаны в терминах входного напряжения фазы.
Выражения 13 и 14 уравнения решения являются
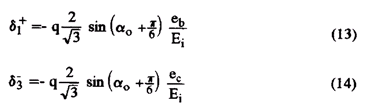
результирующими, которые позволяют определение отношения времени включения, когда q и ao известны.
Таким же образом, используя конфигурации-4, +6, чтобы произвести vo" и установить входной ток
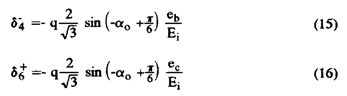
Полученные результаты действительны для

и
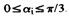
Применяя подобную процедуру для других возможных пар угловых секторов, могут быть определены необходимые конфигурации переключения и отношение времени включения к периоду модуляции каждой конфигурации. Следует отметить, что значения отношения времени включения к периоду модуляции больше чем ноль, как и требуется для выполнимости стратегии управления. Кроме того, сумма этих отношений должна быть ниже, чем единица. Добавляя (13), (14), (15) и (16) с ограничением
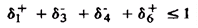
возможно определить максимальное значение отношения передачи напряжения
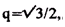
как показано в [2].
Если угол фазы напряжений линии входа и выхода известны, четыре переключающихся конфигурации, требуемые предложенным алгоритмом контроля, могут быть определены. Эти конфигурации используются, пока a, или ao не изменит угловой сектор. Одна из нулевых конфигураций напряжения должна использоваться, чтобы закончить период цикла переключений. Последовательность получающихся пяти конфигураций должна быть определена так, чтобы минимизировать число замен двунаправленного переключателя.
Для значений alfa и alfao рассмотренных на рисунке 2 и 3, доступные комбинации переключения сведены в таблицу II. Простой метод, который позволяет числу замен быть ограниченным, основан на сортировке переключающихся комбинаций так, чтобы
Применение этого метода к рассматриваемому примеру приводит к переключающейся последовательности, показанной в таблице III.
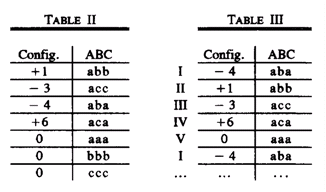
Нужно отметить, что таким образом всего шесть замен требуются в каждый период цикла. Как только конфигурации выбраны и упорядочены, отношение времени каждой конфигурации вычислено, используя выражения 13-16 записанные для соответствующего сектора.
Для матричных преобразователей основное требование это непрерывность тока нагрузки. Кроме того необходимо избегать коротких замыканий на входных зажимах. Для достижения этих целей применяется пошаговая процедура переключения. В [2] и [5] переключающаяся последовательность основана на знаке напряжения между включающейся и выключающейся входными линиями. Безопасная замена может быть также достигнута, используя значение тока нагрузки [6], [7], [8].
В особенности в [6] и [7] методика переключения была основана на присутствии измерения нулевого тока, чтобы гарантировать правильную коммутацию. Эта техника была успешно проверена экспериментально для трехфазного инвертора с ШИМ и могла бы быть применена также для матричного преобразователя 3/3.
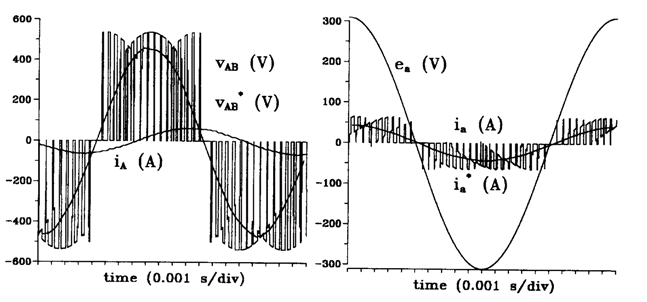
Числовое моделирование матричного конвертера, показанного на рисункне 1, было выполнено, используя программу ATP. Конвертер был смоделирован как ряд идеальных двунаправленных переключателей. Переключающийся алгоритм был осуществлен в ATP согласно принципам, обрисованным в общих чертах в предыдущих разделах. Чтобы подтвердить работоспособность алгоритма управления, моделирование было выполнено для различных режимов работы. Результаты моделирования ATP показывают мгновенное значение напряжение и сглаженные кривые, их гармоническое содержание и представлены на рисунках 4-9. Во всех случаях частота модуляции равна 2 кГц, чтобы четко показать работу преобразователя. Поскольку необходимо представить значение напряжения, используется сглаживание кривых, представляя средние значения за каждый период цикла переключения и дискретным звеном задержки. Рисунок 4 и 5 иллюстрируют результаты в установившихся режимах для входной частоты 50 гц, и выходной частоты 60 гц и отношение передачи напряжения q=0.866. Рисунок 5 ясно четко показывает единичный коэффициент мощности.
Установившийся режим: Входная частота 50 гц, частота нгрузки 60 гц, q=0.866.
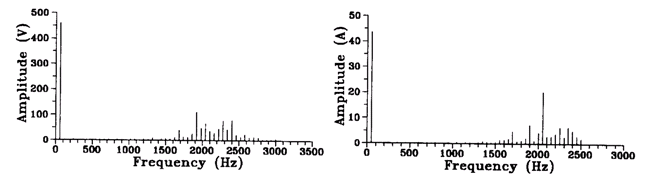
На Рисунке 6 и 7 представлены спектры частот линейного напряжения нагрузки и входного линейного тока. Единственные существенные гармонические компоненты сосредоточены вокруг частоты модуляции.
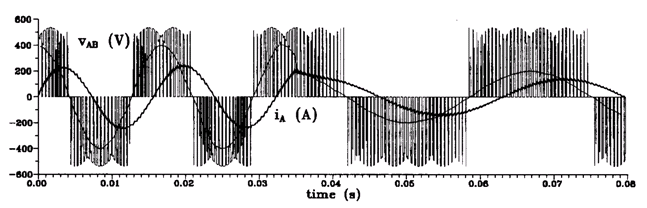
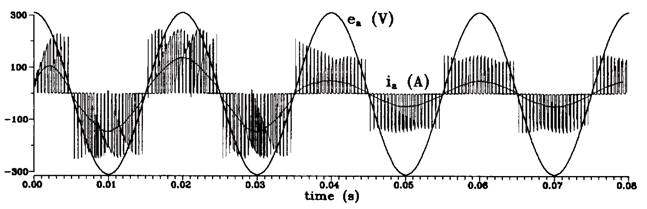
Рисунке 8 и 9 иллюстрируют числовые результаты для изменения частоты и амплитуды выходного напряжения. Частота изменяется мгновенно от 60 гц до 30 гц, в то время как отношение передачи напряжения изменяется от 0.74 до 0.37. Нужно отметить, что начальное отклонение входной формы волны потока от синусоидального происходит из-за начальных переходных процессов.
Переходные процессы при изменении частоты нагрузки (60-30 гц) и коэффициенте передачи напряжения q (0.74-0.37).
В этой рассматривалось применение векторной модуляции, чтобы управлять матричным преобразователем 3/3. Эта техника позволяет регулировать амплитуду выходного напряжения до

амплитуды входного напряжения и управления частотой нагрузки от нуля до максимального значения, ограниченного переключающейся частотой, с поддержанием единичного коэффициента мощности. Возможна отдача энергии в сеть. Были представлены графики процессов и частотный анализ выходного напряжения и входного тока. Входной ток и выходное напряжение являются синусоидальными за исключением высоких гармонических составляющих, связанных с модуляцией. Представленная стратегия управления очень проста и может быть осуществлена в системе микропроцессора с простыми вычислениями. Наконец, знание входных линейных напряжений и использование подходящего закона коммутации реализуют полную компенсацию неуравновешенных питающих напряжений, с отсутствием низкочастотных гармоник. Поведение конвертера при неуравновешенных условиях будет исследовано в будущей работе.

google.ru/url [электронный ресурс]. – Режим доступа: http://www.google.ru/url.