Авторы: Калиев Б.К.
Кызылординский государственный университет им.Коркыт Ата, Казахстан
Источник:Технические науки/6. Электротехника и радиоэлектроника.
В системах автоматизированного проектирования трансформаторов важное место занимают методы моделирования электромагнитных процессов, происходящих в них. Особое внимание уделяется методам анализа режимов работы трансформаторов с учетом нелинейности его параметров. Выбор численного метода имеет существенное значение для успешного решения задачи. Оптимальным является метод, обеспечивающий быструю сходимость решения задачи при наименьшем объеме необходимой памяти ЭВМ. Для различных систем дифференциальных уравнений этот оптимум достигается при различных методах численного интегрирования. Ввиду жесткости дифференциальных уравнений, списывающих режимы работы трансформаторов, эффективным является использование неявных многошаговых методов численного интегрирования. Такие методы обеспечивают эффективное использование средств вычислительной техники на всех этапах расчета – от формирования уравнений трансформатора до получения результатов. Однако использование неявных многошаговых методов требует предварительной подготовки, связанной с приспособлением данного метода для конкретной задачи. При этом важным моментом является формирование дискретных моделей исследуемого объекта [1,2].
В данной работе изложена методика формирования дискретных моделей (ДМ) нелинейных трансформаторов по дифференциальному варианту метода СКП [1,2]. Рассмотрим методику формирования ДМ нелинейных многообмоточных трансформаторов на примере трехобмоточного трансформатора, который получил широкое применение в энергетике. В трехобмоточном трансформаторе также, как и в двухобмоточном, существует поток взаимоиндукции Ф, сцепленный со всеми тремя обмотками, и потоки рассеяния, картина которых отличаются большой сложностью, чем в двухобмоточном трансформаторе, так как приходиться иметь в виду как потоки рассеяния, замыкающейся каждый только вокруг какой-нибудь одной обмотки, так и охватывающие каждый две обмотки.
Дифференциальные уравнения нелинейного трехобмоточного трансформатора учитывающие взаимоиндукции по полям рассеивания, имеют вид:
 (1)
(1) (2)
(2)где R1, R2, R3 - активные сопротивления обмоток, F[Ф] - характеристика намагничивания магнитной цепи трансформатора.
Нелинейная характеристика магнитной цепи F[Ф] трансформатора обусловлено нелинейной зависимости В=f(H) или H=f(В) магнитного материала. Допустим, что аппроксимирующая зависимость задана в виде полиномиальной функции:

где m, n - параметры, зависящие от материалов сердечника исходя из этой характеристики с помощью несложных преобразовании, получим зависимость магнитодвижущей силой F от потока Ф:
 (3)
(3)
учитывая соотношение (3), уравнения магнитной цепи трансформатора (2) перепишем в виде:
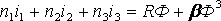 (4)
(4)
Для формирования ДМ продифференцируем соотношение (4):
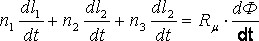 (5)
(5)
Осуществляем переход от заданных уравнений к дискретной математической модели трансформатора на основании методики, предложенный в работе [3]. Согласно упомянутой методике производится замена производных зависимых переменных в исходном уравнений дискретными соотношениями, полученными с помощью дифференциального варианта, метода СКП. В данном случае дискретные соотношения производных тока и потока имеют вид:
 (6)
(6) (7)
(7)Производя замену производных токов и потоков соотношениями (6), (7) получим ДМ нелинейного трехобмоточного трансформатора.
Рассмотрим m – обмоточный нелинейный трансформатор. Считаем, что m обмоток пронизываются общим рабочим потоком Ф, сцепленным со всеми обмотками, а каждая обмотка имеет свой поток рассеяния. При этом допустим, что обмотка не имеет взаимоиндукции по полям рассеяния. С учетом этих условий систему уравнений m – обмоточного трансформатора можно записать в виде:
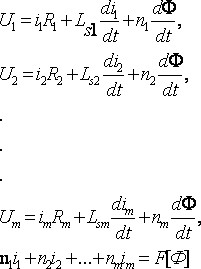 (10)
(10)
Изложенная методика позволяет построить ДМ трехфазных трансформаторов, которые получили широкое распространение в распределительных энергосистемах.
Как известно, в зависимости от устройства сердечника трехфазного трансформатора различают:
а) трансформаторы со связанными магнитными системами;
б) трансформаторы с независимыми магнитными системами;
Для формирования ДМ трехфазных трансформаторов с общим магнитоприводом используем систему дифференциальных уравнений [6]:
 (11)
(11)
где p, e – обозначения фаз A,B,C и a,b,c соответственно. Согласно вышеупомянутой методике ДМ принимает вид
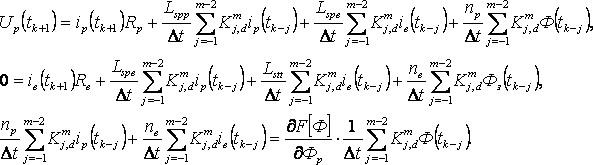 (12)
(12)
Дифференциальные уравнения для каждой фазы трансформатора с независимыми магнитопроводами аналогичны уравнениям двухобмоточного трансформатора [4]:
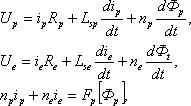
где р, е – обозначения фаз A,B,C и a,b,c соответственно. Следовательно, ДМ таких трансформаторов состоит из трех аналогичных ДМ двухобмоточного трансформатора.
Изложенные способы формирования ДМ позволяют использовать метод СКП для расчета различных процессов в трансформаторах, работающих в нелинейном режиме. При этом в зависимости от режима работы количества обмоток фаз, а также схемы соединений обмоток составляется алгоритм расчета, где реализуется соответствующая дискретная модель.
Литература:
- Бондаренко В.М. О формировании дискретных физических моделей электрических цепей. - Киев: Наук.думка,1978,вып.6-с.107-114.
- Бондаренко В.М. Методы и алгоритмы анализа статистических и динамических режимов нелинейных цепей. - Киев: 1974-105с.
- Бондаренко В.М., Абидов С.Т. Дискретные модели трансформаторов и электрических машин. Техн. электродинамика.- 1983. - №6.-с9-17.
- Фильц Р.В. Математические основы теории электромеханических преобразователей. – Киев: Наук. думка, 1979. – 204 с.