Спиваковский А. О., Дмитриев В. Г.,

ТЕОРИЯ ЛЕНТОЧНЫХ КОНВЕЙЕРОВ

– М.: наука, 1982. [стр. 50 – 51]

2.3 Исследование составляющих

от деформирования груза на конвейерной ленте

и вдавливания роликов в ленту

2.3.1. Сила сопротивления от деформирования груза

Деформирование груза на ленте вследствие его упругого несовершенства приводит к необратимой потере энергии, эквива­лентной некоторой силе сопротивления движению . На современных мощных высокоскоростных конвейерах сила может составлять до 60% от общей силы , поэтому изучение за­висимости этой силы от различных факторов позволит не только более точно рассчитывать общий коэффициент сопротивления движению, но и дать обоснованные рекомендации по выбору пара­метров линейных секции конвейера.

Деформирование груза на ленте представляет собой сложный динамический процесс, зависящий от типа, скорости и амплиту­ды деформирования груза, вида его напряженного состояния и отличающийся в своем поведении от поведения твердых тел. Про­цесс нагружения и разгружения насыпного груза на ленте со­провождается созданием пассивного и активного давлений, отли­чающихся по величине; различная амплитуда и скорость продоль­ных и поперечных деформаций ленты может потребовать при ра­счетах различных реологических констант, а в некоторых случаях и различных реологических моделей для описания груза.

Существуют различные формы проявления внутреннего необратимого рассеяния энергии, среди которых удобна для нашей задачи форма образования замкнутой петли гистерези­са, представляющей нелинейную двузначную зависимость между циклическим напряжением и установившейся циклической дефор­мацией. В этом случае количественной характеристикой проявле­ния внутреннего трения является потребляемая за цикл энергия .

Для описания внутреннего трения вводится коэффициент относительного рассеяния или внутреннего поглощения энергии [40],

определяемый из энергетических соотношений энергия колебательной системы в некоторый момент времени характеризуется величиной , а энергия рассеивается в системе за время , то относительная потеря энергии за цикл равна

(2.15)

где – некоторое текущее значение энергии.

Энергия колебаний определяется следующим образом. Потен­циальная энергия, отнесенная к единице объема деформируемого груза, равна

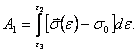(2.16)

Кинетическая энергия, отданнаяпри обратном движении груза:

(2.17)

Разность есть потеря энергии, равная полови­не площади петли гистерезиса.

Аналогично могут быть определены значения энергии ,, на втором полупериоде колебаний

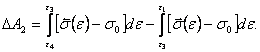(2.18)

В данных интегралах необходимо использовать аналитическуюзависимость , которая может быть получена на основании обработки экспериментальных данных. Тогда представляет собой площадь петли гистерезиса . Следовательно, относительная потеря энергии равна

(2.19)

При этом предполагается, что упругие константы изучаемого тела остаются постоянными; если же они зависят от амплитуды деформаций, частоты и др., то необходимо указывать величины, при которых определено .