АНАЛИЗ ОТКЛОНЕНИЙ НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКИХ СЕТЯХ


Авторы: Майгрус А.А., Дмитриева Е.Н., Куренный Э.Г., проф., д.т.н.
Источник: материалы к Всеукраинской научно–технической конференции студентов «Электротехника, электроника и микропроцессорная техника».

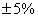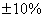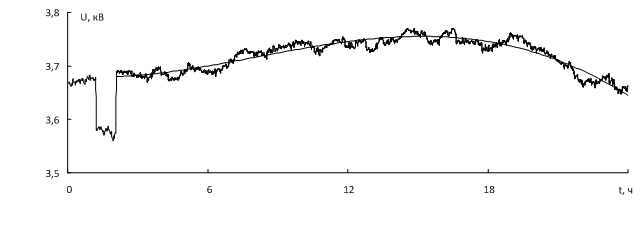
В стандарте [1] устанавливаются нормы на отклонения напряжения (ОН): в нормальном режиме с интегральной вероятностью 0,95 и в предельном режиме с вероятностью 1. Целью работы является разработка методики проверки нормам ГОСТ качества напряжения в действующих электрических сетях. Исходным для анализа является график U(t) одноминутных среднеквадратических значений напряжения (рис. 1).


Рисунок 1 — Суточный график фазного напряжения на шинах 6 кВ

Вероятность выхода ОН за норму 5 % составляет 1–0,95=0,05. Это означает, что допускается превышение нормы в течении 72 мин. за сутки. В [1] не указана интегральная вероятность выхода ОН за нижнюю норму [2]. Примем, что она также равна 0,05. Интегральная вероятность совпадает с ординатой функции распределения F(U) напряжения. В [1] принята процедура обработки по одному суточному графику. Это корректно только для стационарных случайных процессов, характеристики которых не зависят от времени.

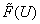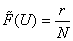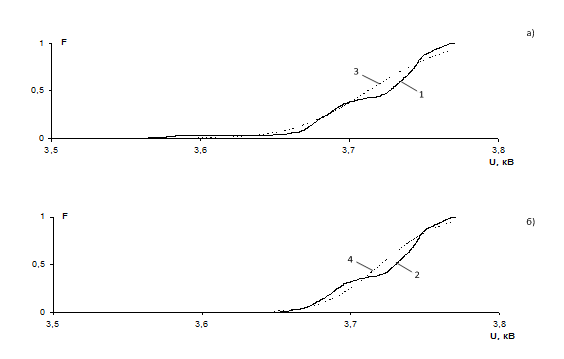
Для определения статистической функции распределения , ординаты графика напряжения в количестве N располагаем в порядке возрастания. Если r=1, 2, … номер ординаты, то . График этой функции представлен на рис. 2,а кривой 1. На начальном участке она имеет почти горизонтальный участок. Это объясняется тем,что в графике напряжения ярко выраженный провал. Если его не учитывать, то этот участок исчезнет (кривая 2 на рис. 2,а).


Рисунок 2 — Функции распределения напряжения с учетом (а) и без учета (б) провала

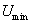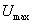Расчетные значения и определяются по ординатам функции распределения, соответствующим абсциссам 0,025 и 0,975. Нормы [1] выполняются, если



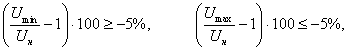
где 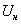— номинальное напряжение.

В рассматриваемом случае расчетный диапазон находится в допустимых пределах. Для предельного режима наименьшая  и наибольшая  ординаты графика напряжения не должны выходить за границы диапазона (0,9; 1,1). Это условие также выполняется.

Перейдем к выбору теоретической модели. Так как на уровень напряжения действует большое количество факторов, вероятное распределение напряжения обычно принимают нормальным. По вычисленным среднему значению и стандарту напряжения была построена кривая 3 нормального закона распределения. Она сильно отличается от статистической кривой 1, прежде всего на начальном участке. Если не учитывать провал, то кривая 4 нормального распределения будет ближе к статистической кривой 2, но расхождения все же есть.

Это можно объяснить тем, что график напряжения является нестандартным, что видно даже по его внешнему виду. С помощью стандартной компьютерной функции был выделен тренд




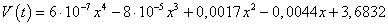
график которого показан на рис. 1 утолщенной линией (без учета провала).

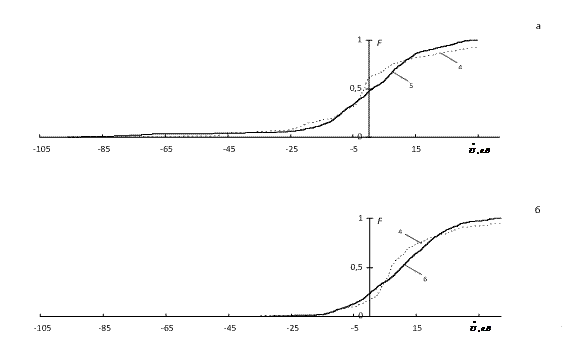
Статистическая функция распределения центрированного процесса



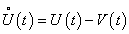
представлена на рис. 3 кривой 4. Функции нормального распределения для центрированного процесса с провалом и без него (кривые 5 и 6) близки к статистическим. Проверка соответствия по критериям согласия будет выполнена позднее после определения количества независимых опытов

Рисунок 3 — Функции распределения центрированных процессов с учетом (а) и без учета (б) провала

В рассматриваемом графике до выделения тренда надо выделять еще и провал, как отдельную составляющую. Однако его появление может быть случайным. Поэтому вероятностную модель целесообразно выбирать по большому количеству суточных графиков напряжения, определяя числовые характеристики и законы распределения для каждого момента времени. Это позволит объективно оценивать нестационарность, обусловленную как трендом, так и выбросами, а также провалами напряжения.

Таким образом, проверку соблюдения норм [1] надо выполнять по статистической функции суточного графика напряжения без его коррекции, а теоретическую модель принимать в виде нестационарного случайного процесса, задаваемого большим количеством суточных графиков напряжения.


Литература
  1. Дмитриева Е.Н. Принцип практической уверенности в задачах электроэнергетики. – Электричество, 2008, №8. – с. 15-21.
  2. ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. - Введ. в Украине с 01.01.2000.