Авторы: Е.Г. Курінний, В.Г. Лєнко
Источник: Технічна електродинаміка. Тем. випуск: Проблеми сучасної електротехніки, 2006, ч. 2. – С. 46—49

ПОСТАНОВКА ЗАДАЧІ

Для енергозберігальний ламп звичайно вказують лише активні потужності. Проте навантаження ламп є несинусоїдальним, тому вони можуть споживати або генерувати реактивну потужність. При цьому збільшується струм в електричній мережі і погіршуються показники електромагнітної сумісності (ЕМС). Метою статті є визначення індивідуальних потужностей окремих ламп і групи ламп, що дозволяє виконувати вибір провідників електричної мережі, перевірку вимог стандартів щодо ЕМС, обґрунтування необхідності і оцінку ефективності засобів стабілізації ЕМС.

У проектуванні система напруг вважається симетричною і синусоїдальною, що значно спрощує аналіз. У діючих мережах наявні завади ЕМС щодо напруги призводять до зміни форми імпульсів струму та розкиду моментів їх появи, що вносить випадковість – як і при керуванні тиристорами [3]. Тому у загальному випадку потрібно переходити до визначення потужностей через кореляційні функції [4,5]. Така задача виходить за рамки статті. Далі прийнято припущення про відсутність завад у напрузі, що за умови виконання вимог стандарту щодо несинусоїдальності напруги є цілком допустимим [6].

Отримані результати очевидним чином розповсюджуються на будь–які однофазні електроприймачі – освітлювальні або силові.

ПОЧАТКОВІ ДАНІ

Початковими даними для розрахунку навантажень групи ламп є графіки миттєвих значень і струму кожної лампи або їх характеристики. Струм лампи є періодичною несинусоїдальною функцією часу з тривалістю циклу tf =0,02 c.

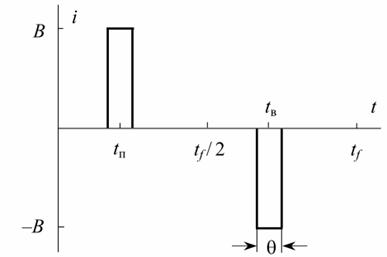
Для короткості розглянемо графік струму у вигляді послідовності різнополярних прямокутних імпульсів величиною В і тривалістю (рис. 1). Через tп і tв позначимо абсциси середин позитивного і від’ємного імпульсів, вважаючи, що різниця між ними дорівнює половині тривалості циклу.

Діюче значення струму лампі

де .

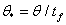При синусоїдальній напрузі повна потужність лампи

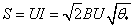
визначається через діючі значення U фазної напруги і струму. Для однієї лампи діюче значення 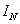струму нульового проводу дорівнює (1).

Знайдемо складові повної потужності. В [7] приведено формулу ряду Фур’є для різнополярних імпульсів, коли вісь абсцис починається з середини позитивного імпульсу. Зробивши переніс вліво початку координат на величину tп, отримаємо ряд

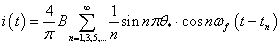де n – номер непарної гармоніки, 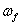– основна кутова частота.

Позначимо через

і представимо ряд у більш зручній для анализу формы:

Активна Р і реактивна Q потужності визначаються по першій гармоніці, яка має фазу 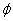і діюче значення

тому

З (3) витікає, що кут дорівнює нулю тоді, коли середина позитивного імпульсу розташована під максимумом кривої напруги. У цьому випадку реактивна потужність відсутня, а лампа споживає найбільшу активну потужність

яка дорівнює повній потужності S f першої гармоніки.

Якщо 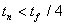то кут є від’ємним. Це означає, що лампа споживає не тільки актину потужність, меншу за (7), але і реактивну потужність. Коли ж 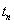перевищує , то активна потужність також менша за (7), але лампа реактивну потужність генерує.

З врахуванням (1), (4) і (5) знайдемо діючі значення струмів гармонік

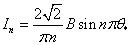
і несинусоїдальної складової

Для лампи потужність спотворень становить

Параметри ламп одного типу і потужності мають деякий розкид, що потрібно враховувати при виборі розрахункового графіку навантажень (див. додаток).

Слід підкреслити, що потужності, які розглянуто, характеризують процес споживання лампою корисної активної потужності. Для оцінки навантажувальної здатності мережі за умови нагріву вводять поняття потужностей у мережі, які визначають втрати активної потужності в мережі.

Оскільки струм лампи протікає по одному фазному і нульовому проводам, за формулою (4.15) з [6] знайдемо повну потужність у мережі

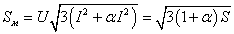де – відношення активних опорів нульового і фазних проводів.

Співвідношення (11) можна записати інакше. Однофазне навантаження у мережі представимо у вигляді струмів прямої, зворотної і нульової послідовностей (індекси І, ІІ, 0). У випадку, що розглядається, їх діючі значення співпадають:

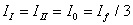Пульсуюча і прихована потужності

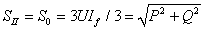співпадають с потужністю прямої послідовності. Повну потужність у мережі знайдемо за флокулою (4.18) з [6]:

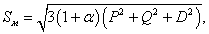що співпадає з (11).

Значення потужностей у мережі можуть використовуватися для оцінки сумарних втрат активної потужності, а не в окремих проводах. Дійсно, одна лампа створює такі втрати потужності у фазному проводі з опором r, нульовому і сумарні:

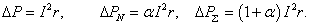Розділивши потужність (11) на 3U, отримаємо струм

еквівалентного симетричного навантаження. По ньому розрахуємо втрати потужності


які співпадають з .

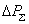Для отримання характеристик сумарних струмів у проводах початковими даними повинні бути проекції струму лампи або його складових на координатні вісі. Дійсну вісь сумістимо з напрямком напруги фази А. Якщо лампу підключено на цю фазу, то проекції струму першої гармоніки на дійсну й уявну вісі з врахуванням (5) становитимуть:

де 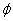– кут між векторами напруги і першої гармоніки струму.

З урахуванням (12) проекції сумарних складових визначаються аналогічними виразами

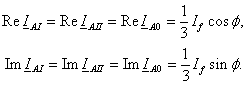Проекції вищих гармонік

Якщо лампу підключено до фази В або С, у формулах (14)—(16) до 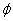і 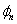потрібно додати кут 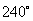або .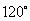

НАВАНТАЖЕННЯ ГРУПИ ЛАМП

Розглянемо спочатку розрахунок навантажень від групи m ламп по графіках їх струмів. Оскільки лампа може бути підключена до будь–якої фази, в базі початкових даних зручно мати три масиви їх струмів, які відрізняються один від одного зсувами на 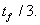. Розрахунок проводиться тільки для одного циклу тривалістю tf.

Струм кожної фази знаходиться підсумовуванням індивідуальних струмів:

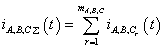де 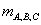– кількість ламп, які підключено до відповідної фази.

Струм у нульовому проводі

Наприклад, якщо три лампи з однаковими графіками струму у вигляді різнополярних імпульсів рівномірно розподілити між фазами, то в кожній фазі будуть протікати однакові струми, але зсунуті на 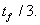.У нульовому ж проводі струм буде являти собою послідовність різнополярних імпульсів, але з циклом 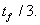, а не tf. Тому в нульовому проводі зали шаться лише гармоніки, кратні трьом.

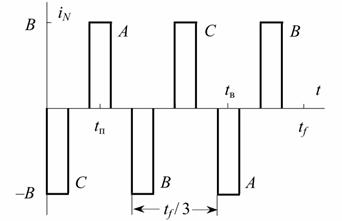
Якщо імпульси не перекриваються (рис. 2), то діюче значення нульового струму буде в 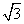рази більшим за діюче значення струму будь–якої фази, яке дорівнює (1). У протилежному випадку струм нульового проводу буде тим меншим, чим більше перекриття суміжних імпульсів, бо вони мають різну полярність.

По графіках сумарних струмів розраховуються будь–які їх характеристики, необхідні для вирішення задач електропостачання.

Перейдемо до розрахунку по характеристиках струмів ламп. У цьому випадку підсумовуються проекції на координатні вісі. Наприклад, з урахуванням (14) струм першої гармоніки фази А від mA ламп при 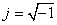буде дорівнювати

Активна і реактивна фазні потужності

де * означає спряжену комплексну величину.

Недоліком розрахунку потужностей спотворень по характеристиках є необхідність визначення параметрів вищих гармонік, бо при цьому виникає питання вибору кількості гармонік, що враховуються. Апріорі його не можна вирішити, оскільки кількість гармонік залежить не тільки від форми графіку струму, але й від кількості ламп, тому що при підсумовуванні абсолютна похибка від неврахування гармонік дуже високого порядку зростає. Окрім того, цей метод не є наочним. У зв’язку з цим доцільно застосовувати метод розрахунку по графіках, згідно якому достатньо визначити лише діюче значення першої гармоніки, а несинусоїдальну складову розраховувати за першим виразом у (9). Навіть коли вищі гармоніки потрібно визначити з метою перевірки виконання вимог стандарту [8], їх розрахунок з використанням сумарного графіку принципово точніше.

ПРИКЛАД

Порівняємо два варіанта освітлення: лампами розжарювання (ЛР, символ ~) потужністю 100 Вт і еквівалентними їм за світовим потоком енергозберігальними лампами типу PL–Electronic 827 потужністю 23 Вт. Живлення здійснюється на напрузі 230 В трьома лампами – по одній на кожну фазу. Навантаження ЛР будемо вважати синусоїдальним, активним. На рис. 3,а для фази А наведено графіки струмів ЛР та PL – останній було записано цифровим осцилографом RECON. Величина = 1,4.

По графіку i(t) лампи PL розрахуємо діюче значення І = 0,173 А, а також струм If = 0,127 А і фазу 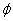= 0,41 рад першої гармоніки. Згідно (9) несинусоїдальна компонента

Потужності лампи PL становлять:

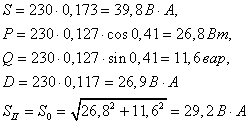Лампа споживає реактивну потужність, а повна потужність на 48,5 % перевищує активну.

Для ЛР маємо:

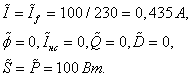По фазних проводах протікають струми однієї лампи. Відношення струмів ламп PL і ЛР становить 0,398. Відношення активних потужностей є ще меншим: 26,8/100 = 0,268.

Сума струмів фаз у варіанті з ЛР дорівнює нулю, а з PL – дає графік, який представлено на рис. 3,б. По ньому знайдемо діюче значення 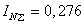А. У нульовому проводі не протікають струми першої гармоніки і гармонік, які не кратні трьом. Проте його струм виявився значно більшим за фазний.

Вищі гармоніки у нульовому проводі мають порядки, кратні трьом. Оскільки імпульси струмів різної полярності при підсумовуванні фазних струмів частково перекриваються, збільшення вищих гармонік однієї лампи стається не у 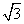, а в меншій мірі.

Ефект енергозбереження від застосування енергозберігальних ламп має дві складові: від меншої активної потужності і зменшення втрат активної потужності в мережі. Зменшення споживання активної потужності відбувається у 100/26,8 = 3,73 разів. Для визначення другої складової знайдемо повні потужності у мережі: у варіанті з ЛР

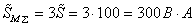а з лампами PL

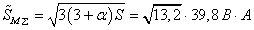Якби від мережі отримували живлення тільки лампи, зменшення повної потужності свідчило б про скорочення втрат активної потужності в мережі у 4,3 рази. Звичайно ж окрім ламп є і інші електроприймачі. У цьому випадку зменшення втрат потрібно оцінювати по паях втрат потужності від ламп у загальних витратах. Ці паї розраховуються по квадратах потужностей згідно [9].

ВИСНОВКИ

1. Несинусоїдальність струмів енергозберігальних ламп суттєво впливає на енергетичні співвідношення у чотирипровідних електричних мережах.

2. Розрахунок потужностей в електричній мережі доцільно виконувати по графіках миттєвих значень струму лампи.

ДОДАТОК

Вплив розкиду параметрів ламп одного типу і потужності розглянемо на прикладі графіка на рис. 1 при незмінних величинах B і та незмінному зсуві між імпульсами, тобто при Sf = const. Випадковою є величина tп і зв’язана з нею 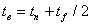. Це дозволяє використовувати лише імовірнісний розподіл цієї величини або кута 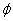. Задача полягає у тому, щоб по щільності розподілу 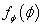або функції розподілу 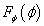кута, які визначаються за даними експериментів, знайти розподіли параметрів режиму.

Порядок розв’язання проілюструємо для активної потужності, вважаючи, що кути знаходяться у діапазоні 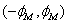, симетричним відносно нульового значення. Поточному значенню 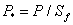потужності у відносних одиницях відповідають дві абсциси:

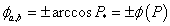Функція розподілу

у межах 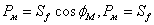де враховано, що

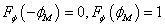Аналогічно при 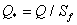знайдемо функцію розподілу реактивної потужності

у межах

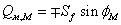Звичайно при розрахунках параметрів приймають нормальний закон розподілу для випадкової величини 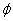. Діапазон значень кута є нескінченним, а тому теоретично потрібно було б розглядати абсциси від 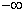до 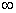. Проте за змістом задачі розкид кута не може перевищувати 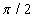, тому розрахункове значення . Його можна прийняти за відомим правилом трьох сигм

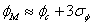де 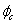і 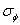– середнє значення і стандарт розкиду кута. Це дозволяє використати формули (Д.1) і (Д.3), які приймають вигляд

де 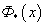– табульована функція стандартного нормального розподілу.

Розрахункові діапазони 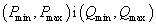згідно з принципом практичної впевненості з межовою імовірністю Еx визначають з рівнянь:

Звичайно приймають 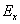= 0,05. Якщо різниця між мінімальним і максимальним значенням є суттєвою, то розрахунки параметрів режиму потрібно виконувати для границь розрахункових діапазонів. У протилежному випадку розрахунковий графік струму природно віднести до середнього значення кута.

Литература

1. Е.Г. Курінний, В.Г. Лєнко, «Електромагнітна сумісність. Доза пульсацій», // Світлотехніка та електроенергетика, с. 48—53, № 5, 2005.
2. В.Г. Лєнко, «Ефективність застосування енергозберігальних ламп за дозою флікеру напруги», // Наукові праці Донецького нац. техн. університету. Серія «Електротехніка і енергетика», вип. 98, Донецьк, с. 106—110, 2005.
3. Ю.М. Быков, В.С. Василенко, «Помехи в системах с вентильными преобразователями», М: Энергоатомиздат, 152с., 1986.
4. «Баланс энергий в электрических цепях», / В.Е. Тонкаль и др., Киев: Наукова думка, 312 с., 1992.
5. В.П. Комлев, С.И. Малафеев, «О статистическом подходе к анализу энергетических характеристик нелинейных электрических цепей», // Электричество, с. 33—36, № 1, 1987.
6. Р. Дрехслер, «Измерение и оценка качества электроэнергии при несимметричной и нелинейной нагрузке», М: Энергоатомиздат, 112 с., 1985.
7. Л.А. Бессонов, «Теоретические основы электротехники», М: Высшая школа, 750 с., 1964.
8. ГОСТ 13109–97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
9. О.М. Дмитрієва, О.В. Левшов, «Оцінювання пайової участі споживачів у втратах електроенергії», // Наукові праці Донецького нац. техн. університету. Серія «Електротехніка і енергетика», вип. 67, Донецьк, с. 47—50, 2003.