Авторы: Куренный Э.Г., Ленко В.Г.
Источник: XXXIV Miedzynarodowa Konferencja: Telecommunication and Safety Systems in Mining. ATI 2006. Sekcji Cybernetyki w Gornictwie KG PAN. – Poland: Szczyrk, 31 May – 2 June 2006. – P. 219—226

1. ПОСТАНОВКА ЗАДАЧИ

Изменение освещенности вызывает дополнительное утомление людей, что приводит к уменьшению производительности и ухудшению зрения. Допустимость низкочастотной модуляции освещенности вследствие колебаний действующих значений напряжения в электрической сети частотой до 35 Гц оценивают дозой фликера напряжения [1]. Во фликер–модели используются параметры стандартной лампы накаливания 60 Вт, 230 В. Такой подход допустим при контроле ЭМС в точках коммерческого учета электроэнергии. На предприятиях необходимо учитывать параметры фактических ламп. В [2—4] это осуществлялось пересчетом передаточной функции линейной части фликер–модели. Такой подход осуществим при определении доз фликера расчетным путем. Для целей же измерения невозможно ввести во фликерметр параметры всех ламп разных типов и мощностей.

Допустимость изменения мгновенных значений (пульсации) освещенности e(t) оценивают коэффициентом пульсации Ke, который измеряется в процентах от средней освещенности ea и пропорционален диапазону 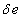пульсации. Этот показатель не учитывает форму и частоту пульсации. При одном и том же Ke прямоугольная пульсация больше сказывается на человеке, чем синусоидальная, а треугольная – меньше. С увеличением частоты негативное воздействие пульсации уменьшается.

Недостатки существующих способов оценивания ЭМС требуют разработки универсальных показателей ЭМС.

2. ДОЗА ФЛИКЕРА ОСВЕЩЕННОСТИ

В [1] приведена передаточная функция взвешивающего фильтра (WF), которую запишем в виде

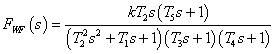где k = 1,74802, Т1 = 0,015418 с, Т2 = 0,017385 с, Т3 = 0,12989 с, Т4 = 0,007267 с, Т5 = 0,069811 с. Для обеспечения единства результатов измерений и расчетов необходимо учесть передаточные функции фильтров HF высших и LF низших частот:




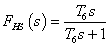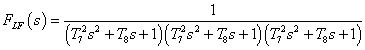
с постоянными времени: Т6 = 3,1831 с, Т7 = 0,004573 с, Т8 = 0,0023537 с, Т9 = 0,0064308 с, Т10 = 0,0087849 с.

Полная передаточная функция линейной части фликер–модели со стандартной лампой определяется по формуле

где 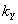= 16 (%)—1 – коэффициент перехода от % к относительным единицам.

Стандартная лампа имеет передаточную функцию

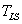где – коэффициент передачи, – постоянная времени.

Если лампа имеет передаточную функцию H (s), то переход от (4) к передаточной функции линейной части фликер–модели с фактической лампой очевиден (например, формула (9) в [3]):

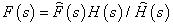В формуле (3) из [3] амплитудно–частотная функция (AFF) лампы определена как отношение действующих значений освещенности и квадратов напряжения. На наш взгляд, такой подход не может быть принят. В самом деле, понятие передаточной функции относится к линейным системам. В линейном WF напряжение в квадрат не возводится, поэтому и в знаменателе формулы для AFF надо брать напряжения, а не их квадраты.

Выясним соотношение между коэффициентами передачи при разных подходах. Если брать напряжение U* в относительных единицах (символ *), то освещенность

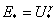где 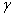– постоянный коэффициент. Линеаризация в точке U* = 1 дает

Дифференцирующие звенья в (1) и (2) не пропускают постоянную составляющую, поэтому . Коэффициент 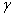и является коэффициентом передачи в модели лампы.

Если же исходить из квадратов напряжения, то 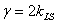. Следовательно, использование вместо 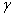занижает дозу фликера вдвое, хотя отношение передаточных функций ламп в (6) остается без изменения.

На рис. 1 представлена статическая характеристика ламп накаливания Е27СL 60 Вт, 230 В. Если экспериментальные точки, показанные светлыми кружками, относить к напряжению, то аппроксимирующая кривая 1 описывается выражением (7) при 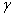= 3,8. Если использовать квадраты напряжений, то кривая 2 описывается тем же выражением, но с коэффициентом 1,9.

В формуле (9) из [3] приняты следующие параметры стандартной лампы: 1,9 – коэффициент передачи, 0,023 с – постоянная времени. Далее вместо (5) используется выражение

с 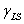= 3,8 и той же постоянной времени 0,023 с.

Для инженерных целей параметры фактических ламп удобно учитывать путем введения коэффициентов cL пересчета доз фликера 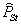со стандартной лампой к дозам

с фактическими лампами. В этом случае вместо (6) передаточные функции имеют вид

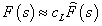Разумеется, такой подход не является строгим, так как соотношение зависит как от параметров моделей ламп, так и от частотного спектра колебаний напряжения (дискретного или непрерывного). Учитывая, что максимум AFF исходной фликер–модели равен единице, коэффициенты пересчета можно принять равными максимумам AFF моделей с фактическими лампами – несмотря на несовпадение резонансных частот и непропорциональность AFF.

Достоинством инженерного решения является то, что сохраняется существующая фликер–модель – как базовая, а фликерметр не переделывается. Тем не менее, вследствие неточности решения более перспективным представляется другой подход, основанный на том, что из фликер–модели вообще исключается модель лампы. В этом случае помехой являются не колебания напряжения, а колебания действующих значений освещенности. Поэтому вместо дозы фликера напряжения введем понятие дозы фликера 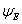освещенности.

Соответствующая Е–фликер–модель отличается от модели фликера напряжения входным блоком и передаточной функцией линейной части.

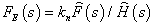Коэффициент нормировки kn обеспечивает равенство единице AFF линейной части модели при резонансной частоте , которая отличается от 8,8 Гц. Коэффициент есть обратная величина от значения AFF стандартной лампы при этой частоте:

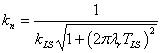Допустимое значение дозы .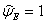

3. ДОЗЫ ПУЛЬСАЦИИ ОСВЕЩЕННОСТИ

Пульсация, как и фликер, вызывает утомление человека. Поэтому по аналогии с дозой фликера введем понятие дозы пульсации 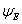. Помехой здесь является пульсация, в связи с чем модель лампы не требуется. Анализ экспериментальных данных показал, что при синусоидальной пульсации амплитуда реакции y(t) фильтра WF обратно пропорциональна частоте 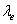. Такую реакцию можно моделировать инерционным звеном с постоянной времени Тe, которая должна удовлетворять неравенству = 1 или 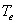= 0,0016 c.

Примем Тe = 0,02 с. Коэффициент передачи ke в AFF инерционного звена определим позже.

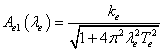Чтобы исключить низкочастотную модуляцию, которая оценивается дозой фликера, необходимо предусмотреть фильтр высших частот, который для определенности примем в виде полиномиального фильтра второго порядка с AFF

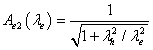
с частотой среза = 25 Гц.

AFF линейной части модели пульсации равен произведению (11) и (12):

Этой AFF соответствует передаточная функция

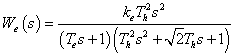
с постоянной времени .

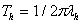При частоте 100 Гц выражение (11) должно давать единицу, что позволяет найти коэффициент передачи ke= 12,6307. Нетрудно убедиться, что

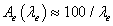
Постоянная времени блока 4 фликерметра [1], равная 0,3 с, намного превышает наибольшую длительность цикла 0,01 с при наименьшей частоте 100 Гц. По этой причине процесс на выходе блока SS практически не изменяется и мало отличается от квадрата стандарта на выходе линейной части модели. Это делает статистическую обработку излишней, а дозу пульсации позволяет определять по формуле

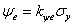Коэффициент пропорциональности 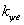найдем из условия равенства допустимой дозы единице при работе человека с наибольшим зрительным напряжением. В этом случае допустимое значение коэффициента пульсации 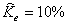. Отнесем это значение к синусоидальной пульсации частотой 100 Гц, когда AFF равна единице, а стандарт реакции в раза меньше коэффициента пульсации. В результате из (15) получим 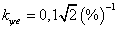. Для других условий зрительной работы допустимые дозы 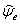будут увеличиваться пропорционально отношению соответствующих значений коэффициентов пульсации к 10 %.

Условие ЭМС имеет вид:

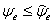
4.РАСЧЕТ И ИЗМЕРЕНИЕ ДОЗ

В проектировании исходными данными для расчетов доз фликера являются процессы изменения во времени действующих значений напряжения или их характеристики. Дозы пульсации рассчитываются по процессам e(t) каждой лампы. Измерение доз производится либо специализированными приборами, либо вначале записываются процессы изменения напряжения и (или) освещенности, а затем по ним рассчитываются дозы.

При одной и той же помехе результаты измерений и расчетов должны совпадать. Это обеспечивается тем, что структурные схемы динамических моделей ЭМС, используемые в расчетах, и структурные схемы измерительных приборов должны быть одинаковыми. Например, поскольку во фликер–метре есть частотные фильтры, то расчет доз фликера надо производить с использованием передаточной функции (4), а не (1). Разница в результатах зависит от частотного спектра помехи. Так, в случае с прямоугольными колебаниями частотой более 12 Гц без учета фильтров потребуется рассчитывать все гармоники, а с учетом фильтров – только первую, так как все высшие гармоники имеют частоты, меньшие 35 Гц.

Расчет доз целесообразно выполнять методом парциальных реакций [5], согласно которому линейная часть динамической модели ЭМС представляется параллельно включенными инерционными звеньями первого порядка. Количество звеньев равно порядку многочлена в знаменателе передаточной функции: 11 – в (4), 3 – в (14). Параметры звеньев определяются по полюсам знаменателя. Парциальные реакции на выходе звеньев суммируются. При периодических колебаниях парциальные реакции определяются для стационарного режима без расчета переходного процесса. Для этого используются условия равенства ординат в конце предыдущего и начале последующего участков процесса изменения напряжения внутри цикла.

Для периодических помех решение может быть найдено и методами гармонического анализа. При расчете доз фликера напряжения или освещенности требуется суммировать гармоники с их фазами, что снижает эффективность применения рядов Фурье. Для определения же доз пульсации достаточно знать только действующие значения En гармоник. К тому же AFF (15) быстро убывает с увеличением номера n гармоники, поэтому количество N учитываемых гармоник невелико. С учетом (15) и (16) доза пульсации

Оценивание по дозе обычно менее жесткое, чем по коэффициенту пульсации, так как гармоники реакции при n > 1 существенно меньше, чем гармоники пульсации. Например, для одной из энергосберегающих ламп график пульсации близок к сглаженной трапеции со следующими характеристиками: Ke = 7,4 %; при n = 1, 2 и 3 действующие значения гармоник равны 4,5; 1,706 и 0,487. В этом случае формула (16) дает 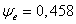. Остальные гармоники мало сказываются на величине дозы. Коэффициент пульсации меньше 10 %, а доза меньше единицы. Следовательно, условие ЭМС не нарушается. Однако коэффициент пульсации меньше допустимого значения только в 10/7,4=1,35 раза, а доза в 1/0,458=2,18 раза.

5. ТЕХНИКО–ЭКОНОМИЧЕСКОЕ СОПОСТАВЛЕНИЕ ЛАМП

Для обоснования целесообразности применения тех или иных ламп необходимо сопоставить разницу в их стоимости и издержками на эксплуатацию с эффектом от улучшения ЭМС. Если для конкретного производства составляющая экономического эффекта от увеличения производительности труда находится экспериментально, то экономические последствия от ухудшения зрения могут быть оценены только путем экспертных оценок.

Возможен следующий подход. За основу берется среднестатистический страховой взнос В на случай потери зрения. Ежегодный ущерб Y зависит от суммы

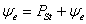
доз фликера напряжения (или освещенности). При отсутствии колебаний и пульсации доза равна нулю, поэтому искомую зависимость примем в виде

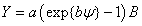
Коэффициенты а и b найдем из двух условий: при 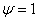ущерб составляет заданную долю 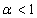от В, а при некотором значении ущерб равен В. В результате получим трансцендентное уравнение

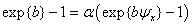
для определения b. Второй коэффициент

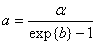Нами рекомендуются значения 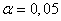и 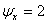, при которых a= 0,002778 и b = 2,9445.

Использование зависимости (19) позволяет экономически обосновать целесообразность применения более дорогих ламп, но имеющих лучшие показатели ЭМС по дозам фликера и пульсации.

6. ЗАКЛЮЧЕНИЕ

Доза фликера напряжения со стандартной лампой накаливания является условным показателем ЭМС, применимым лишь для оценивания ЭМС в точках коммерческого учета электроэнергии. Исключение из фликер–модели стандартной лампы позволяет ввести универсальный показатель допустимости колебаний освещенности – дозу фликера освещенности, которая учитывает фактические условия освещения (тип и количество ламп, распределение их по фазам и др.).

Коэффициент пульсации освещенности не учитывает форму и частоту пульсации. Допустимость пульсации целесообразно уценивать по универсальному показателю – дозе пульсации освещенности.

Расчет и измерение доз производится в рамках единых динамических моделей, что позволяет обеспечить единство результатов измерения и расчета доз. Расчет доз фликера напряжения или освещенности рекомендуется выполнять методом парциальных реакций, а доз пульсации – с использованием рядов Фурье.

Эффективность ламп разного типа оценивается с учетом их стоимости, срока службы и ущерба от колебаний и пульсации освещенности. Помимо составляющей ущерба от уменьшения производительности целесообразно учесть составляющую ущерба от ухудшения зрения, что повысит конкурентноспособность дорогих ламп с лучшими показателями ЭМС.

Литература

1. CEI/IEC 61000—4—15. Electromagnetic compatibility – Part 4, Section 15: Flickermeter – Functional and design specification. 1997.
2. Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. – Киев: Наукова думка, 1984. – 271 с.
3. Brauner G., Hennerbichler C. Lamp models for flicker simulation and illumination planning. – Fifth International Conference: Electrical Power Quality and Utilisation. – Cracow, 1999.
4. Куренный Э.Г., Дмитриева Е.Н., Куренный Д., Цыганкова Н.В. Совершенствование модели фликера. – Электричество, 2003, № 2.
5. Kourennyi E.G., Petrosov V.A., Chernikova L.V. Linear filtration on random processes in EMC models: the “partial reaction” method. – Fifteenth International Wroclaw symposium and exhibition: Electromagnetic compability 2000. – Wroclaw: National Institute of Telecommunications, 2000, part II.