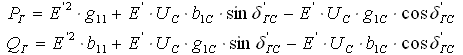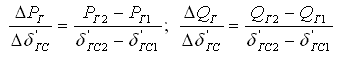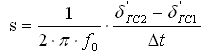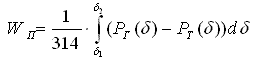Подпорина Анастасия Игоревна

Электротехнический факультет

Кафедра Электрических систем

Специальность «Электрических систем и сетей»

Исследование возможностей использования технологии СМПР для управления переходными режимами электрических систем

Научный руководитель: Заболотный Иван Петрович

Содержание

1. Введение
2. Идентификация матрицы СВП в режиме реального времени
3. Контроль пропускной способности сети и коэффициентов запаса устойчивости
4. Управление для предотвращения нарушений устойчивости с контролем запасов устойчивости в режиме реального времени
5. Литература

     Развитие электроэнергетических систем (ЭЭС) сопровождается усложнением технологических задач управления режимами. Особые сложности вызывает решение задач реального времени, т.е. управление режимами ЭЭС в темпе реального процесса. Управление режимами ЭЭС направлено на обеспечение надежности режимов и живучести системы, которая оценивается ее способностью противостоять возмущениям. Поэтому управление переходными режимами, в том числе и аварийными, всегда являлось актуальной задачей.
     Технология управления переходными режимами ЭЭС постоянно развивается, что обусловлено наличием несоответствия между требованиями к управлению и возможностями используемой технологии управления. Усложнение условий функционирования ЭЭС приводит к проблемам в решении задачи обеспечения надежности и живучести, а появление новых технологий создает условия для совершенствования системы управления.
     Использование современных математических методов и средств микропроцессорной техники позволило существенно повысить уровень управления переходными режимами в целом, но эффективность решения задач в темпе повысилась незначительно.
     Эффективность управления на основе математического моделирования определяется не только адекватностью математических моделей элементов и режима в целом, не только достоверностью исходной информации и скоростью ее поступления в систему управления, но и гибкостью математической модели адаптироваться к текущей ситуации и цели управления. Существующая неопределенность информации, сложности учета множества различных факторов в реальной энергосистеме определяли необходимость энергетиков страховаться и предусматривать дополнительные запасы при настройке порогов срабатывания систем противоаварийной автоматики, что в конечном итоге ведет к недоиспользованию первичного оборудования, что противоречит требованиям эффективности управления в условиях рыночных отношений в электроэнергетике.
     В последние годы в ЭЭС интенсивно внедряются технология гибких линий электропередач и технология мониторинга переходных процессов – Wide Area Measurement Systems (СМПР – WAMS). СМПР реализует технологию векторного измерения параметров режима ЭЭС с высокой точностью и с обеспечением синхронизации измерений, что является одной из приоритетных технологий развития крупнейших энергосистем мира.
     В ряде работ отмечаются перспективные направления использования СМПР. Одним из направлений использования является обеспечение качественно нового уровня моделирования за счет верификации и коррекции моделей на основе текущего режима и использования данных о протекании переходных режимов в энергосистеме в методах распознавания эталонов режимов.

Актуальность темы

     Появление и развитие технологии СМПР было обусловлено несколькими факторами:

• усложнением топологии и структуры электроэнергетических систем, приводящим к усложнению динамических процессов, происходящих в них при технологических нарушениях;

• повышением количества и увеличением тяжести крупных системных аварий. Для разработки мер по их предотвращению и восстановлению систем после аварий необходим глубокий анализ причин, породивших эти аварии и характера их протекания, что невозможно без детального анализа динамического поведения системы;

• появление и широкое внедрение технологии глобального позиционирования объектов (Global Positioning System, GPS), которая позволила синхронизировать измерения и получить такой важный для динамического анализа параметр, как взаимный угол напряжения, который не удавалось получить с помощью существующих систем информационного обеспечения.

     Благодаря синхронности измерений в СМПР появляется возможность контролировать параметры, характеризующие взаимное движение синхронных машин во время динамического перехода: взаимные углы между векторами электродвижущих сил (ЭДС) генераторов, взаимные скольжения, ускорения, синхронизирующую мощность. Указанные параметры обладают наибольшей информативностью с точки зрения оценки запасов устойчивости и реализации противоаварийного управления в энергосистемах.
     Новые возможности управления устойчивостью возникают при идентификации в режиме реального времени на основе этих параметров матрицы собственных и взаимных проводимостей (СВП) генераторов, связанных электрической сетью, как модели управления устойчивостью режима.
     Этими факторами определяется актуальность темы настоящей работы, в которой исследуется целесообразность и принципиальная реализуемость такого управления в энергосистемах на примере системы «станция – шины бесконечной мощности».



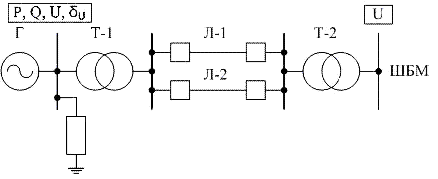
Рис. 1 — Схема моделируемой ЭЭС

Цель работы: исследование возможностей использования технологии СМПР для управления переходными режимами.

Основные задачи исследований:

• проанализировать методики использования СМПР для идентификации модели управления энергосистемой;

• оценить эффективность определения матрицы собственных и взаимных проводимостей генератора на основе СМПР.

Объект исследований: электроэнергетическая система в условиях электромеханических переходных режимов.

Предмет исследований: применение векторного представления электрических величин в переходных режимах электроэнергетических систем.

Методика и методы исследований: В работе используются методы численного решения нелинейных алгебраических и дифференциальных уравнений для расчетов установившихся и переходных режимов работы электрических систем, действующие методики анализа режимов ЭЭС. Моделирование режимов работы ЭЭС выполнялось с использованием математического пакета программ Mathcad.

Научная новизна: Научная новизна заключается в усовершенствовании математических моделей синхронных генераторов и в целом электрических станций, разработки методов их использования для определения матриц собственных и взаимных проводимостей.

Обзор исследований и разработок по теме
     СМПР представляет собой комплекс регистрирующих приборов, каналов передачи информации между регистраторами, концентраторами данных и центрами управления, а также средств обработки полученной информации. Регистраторы устанавливаются в крупных энергоузлах, на межсистемных связях, на электростанциях вторичного регулирования.

1 ИДЕНТИФИКАЦИЯ МАТРИЦЫ СВП В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ

     Контроль параметров переходного процесса с помощью СМПР позволяет выполнить идентификацию модели управления энергосистемой в режиме реального времени. Задача идентификации модели управления предполагает определение матрицы СВП, решение которой можно рассмотреть на примере простейшей схемы «генератор с собственной нагрузкой – ШБМ» (рис. 2). К основным измеряемым параметрам относятся модули и углы напряжений по концам контролируемой электропередачи, активная и реактивная мощности в узле генерации.




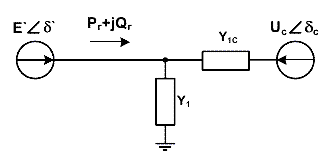
Рисунок 2 — Эквивалентная схема замещения

     Определение СВП основано на использовании известных выражений, в которых активная и реактивная мощности линейно зависят от СВП:



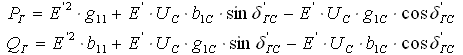
     где: q_1C,b_1C, – активная и реактивная взаимные проводимости,

       q₁₁, b₁₁ ,– активная и реактивная собственные проводимости. Собственные и взаимные проводимости связаны соотношениями: q₁₁=q₁+q_1C; b₁₁=b₁+b_1C.

     Дополнив уравнения (1) уравнениями для производных:



     получаем систему линейных уравнений, решение которой при допущении постоянства переходной ЭДС дает матрицу СВП.
     Поскольку производные 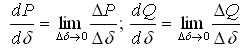 активной и реактивной мощности по взаимному углу приближенно могут быть определены по приращениям мощности и угла (в установившихся режимах – при нерегулярных колебаниях нагрузки и роторов генераторов, в переходных режимах – в процессах их протекания):



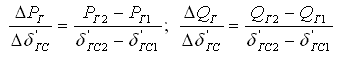
     Блок – схема алгоритма идентификации матрицы СВП представлена на рис. 3.



Рис. 3. Блок–схема алгоритма идентификации матрицы СВП

2 КОНТРОЛЬ ПРОПУСКНОЙ СПОСОБНОСТИ СЕТИ И КОЭФФИЦИЕНТОВ ЗАПАСА УСТОЙЧИВОСТИ


     Матрица СВП позволяет использовать угловые характеристики мощности для определения пределов передаваемых мощностей по контролируемым сечениям, запасов статической и динамической устойчивости для генераторов в режиме реального времени.
     Оценка динамической устойчивости и ее запаса может быть выполнена по энергетическому критерию по отношению к взаимному движению роторов.
     Для простейшей системы «станция – ШБМ» кинетическая энергия, запасенная эквивалентным генератором в относительном движении, может быть определена как:



     где: T_j — постоянная механической инерции агрегата,
            P_ном — номинальная мощность генератора, МВт,
            s — скольжение ротора генератора, о.е., которое можно вычислить приближенно, если перейти от дифференциалов к приращениям:



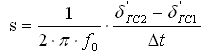
     Максимально возможную энергию торможения, необходимую для оценки динамической устойчивости и ее запаса, можно получить путем интегрирования угловой характеристики мощности, полученной по найденным значениям матрицы СВП:



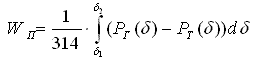
     где:
          P_Г(δ) – электрическая мощность генератора, МВт;
          P_Т(δ) – мощность турбины, МВт.

     В общем случае мощность регулируемой турбины не может быть представлена зависимостью P_Т(δ). В этом случае определение энергии торможения связано с определенными трудностями, ввиду нелинейного характера изменения мощности турбины во времени и, соответственно, в координатах мощности и взаимного угла.
     Аналитическое решение этой задачи может быть получено, если выполнить аппроксимацию кривой P_Т(δ) полиномом. Степень аппроксимирующего полинома будет зависеть от скорости изменения мощности турбины, о которой можно судить по экспериментально снятым моментно-импульсным характеристикам турбины.

3 УПРАВЛЕНИЕ ДЛЯ ПРЕДОТВРАЩЕНИЯ НАРУШЕНИЙ УСТОЙЧИВОСТИ С КОНТРОЛЕМ ЗАПАСОВ УСТОЙЧИВОСТИ В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ

     Применительно к задаче управления ИРТ (Импульсная Разгрузка Турбины) идентификация матрицы СВП в послеаварийном режиме позволяет:

• выполнить оценку достаточности глубины ИРТ для обеспечения динамической устойчивости электропередачи;

• принять решение о необходимости более глубокой РТ или отключения части генераторов, если запас по динамической устойчивости недостаточен;

• определить уровень восстановления мощности турбины по условию 8%-го запаса статической устойчивости в послеаварийном режиме.

     В ряде работ используются простейшие схемы электроэнергетических систем в условиях электромеханических переходных режимов. В моей работе предполагается оценить эффективность методов на более сложных схемах, используя программу Power Factory.

Примечание
     При написании данного автореферата магистерская работа не была завершена. Окончательное завершение: декабрь 2011 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.


Литература
1. Тундаева Д.В. Применение системы мониторинга переходных режимов для идентификации модели управления энергосистемой // Наука. Технологии. Инновации: Матералы всероссийской научной конференции молодых ученых. — Новосибирск: Изд–во НГТУ, 2007. Ч.3. С. 254–256.
2. Аюев Б.И., Куликов Ю.А. Перспективные направления использования системы мониторинга переходных процессов ЕЭС/ОЭС // Труды международной конференции «Релейная защита и авоматика энергосистем». — Чебоксары, 9–13 сентября 2007.
3. Касобов Л. С. Моделирование и учет ограничений по устойчивости для энергосистемы Таджикистана / Л. С. Касобов, науч. рук. А. Г. Фишов // Наука. Технологии. Инновации: Материалы всероссийской научной конференции молодых ученых в 7–ми частях. Новосибирск: Изд–во НГТУ, 2008. – Ч.3. С. 165–167.
4. Б.С. Стогній, О.В. Кириленко, О.Ф. Буткевич, М.Ф. Сопель. Організація моніторингу режимів енергооб’єднання України та нові можливості розв’язання задач диспетчерського керування. Журнал «Наука та інновації» №6,2009.
5. Аюев Б.И., Ерохин П.М., Куликов Ю.А. Система мониторинга переходных режимов ЕЭС/ОЭС // Технологии управления рее жимами энергосистем XXI века: Сб. докл. Всеросс. Научнопракт. конф. / Под ред. А.Г. Фишова. — Новосибирск: Изддво НГТУ, 2006. — С. 83–92 с.
6. Журавлев Д.М. Исследование и разработка применения векторного представления электрических величин в переходных режимах электроэнергетических систем. Автореферат. [Электронный ресурс]. — Режим доступа: http://www.dissercat.com/content/issledovanie-i-razrabotka-primeneniya-vektornogo-predstavleniya-elektricheskikh-velichin-v-p
7. Касобов Л.С. Оценка технической и єкономической єффективности управления режимами ЄЄС для предотвращения нарушений устойчивости. [Электронный ресурс]. — Режим доступа: http://elib.altstu.ru/elib/books/Files/pa2009_2/pdf/056kasobov.pdf